Có bao nhiêu số nguyên m để hàm số y 1/3.x^3 - mx^2 + x - 1 đồng biến

❮ Bài trước Bài sau ❯

Câu hỏi:

Có bao nhiêu số nguyên m để hàm số $y = \frac{1}{3} x^{3} - m x^{2} + x - 1$ đồng biến trên $ℝ$ ?

A. 2

B. 4

C. 3

D. 5

Trả lời:

Đáp án C

Xét hàm số $y = \frac{1}{3} x^{3} - m x^{2} + x - 1$ . Ta có tập xác định $D = ℝ$

Đạo hàm $y^{'} = x^{2} - 2 m x + 1$

Để hàm số đồng biến trên $ℝ$ thì $y^{'} \geq 0$ , $\forall x \in ℝ$ và $y^{'} = 0$ tại hữu hạn điểm trên $ℝ$

Điều này xảy ra khi và chỉ khi $Δ^{'} = m^{2} - 1 \leq 0$ (do $a = 1 > 0$ )

$m^{2} - 1 \leq 0 \Leftrightarrow - 1 \leq m \leq 1$ . Vậy có 3 số nguyên thỏa yêu cầu bài toán.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Trong các hàm số sau, hàm số nào nghịch biến trên $(1; + \infty)$ ?

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) có đạo hàm trên $ℝ$ và $f^{'} (x) < 0, \forall x \in (0; + \infty)$ . Biết $f (1) = 2020$ . Khẳng định nào sau đây đúng

Xem lời giải »

Câu 3:

Cho hàm số $y = \frac{2 x - 1}{x + 2}$ . Khẳng định nào dưới đây là SAI?

Xem lời giải »

Câu 4:

Hàm số nào dưới đây đồng biến trên khoảng $(0; + \infty)$

Xem lời giải »

Câu 5:

Hàm số $y = x^{3} + 3 x^{2} + m x + m$ đồng biến trên tập xác định khi giá trị của m là:

Xem lời giải »

Câu 6:

Giá trị của m để hàm số $y = \frac{m x + 4}{x + m}$ nghịch biến trên mỗi khoảng xác định là:

Xem lời giải »

Câu 7:

Cho hàm số $y = f (x)$ có đạo hàm $f^{'} (x)$ trên khoảng $(- \infty; + \infty)$ . Đồ thị của hàm số $y = f^{'} (x)$ như hình vẽ. Hàm số $y = f (x)$ nghịch biến trên khoảng nào trong các khoảng sau?

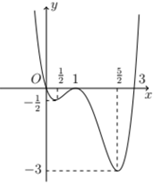
Xem lời giải »

Câu 8:

Cho hàm số y = f(x) có đạo hàm trên $ℝ$ và $f' (x) > 0, \forall x \in (0; + \infty)$ . Biết f(1) = 2. Khẳng định nào dưới đây có thể xảy ra?

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Có bao nhiêu số nguyên m để hàm số y 1/3.x^3 - mx^2 + x - 1 đồng biến

Xem thêm bài tập Toán có lời giải hay khác: