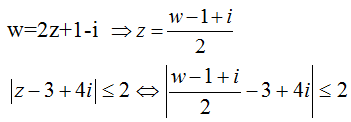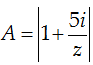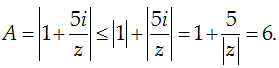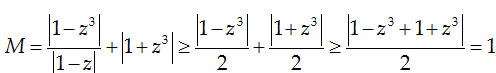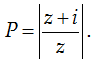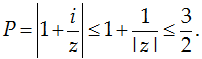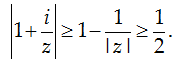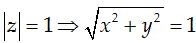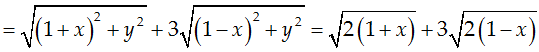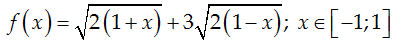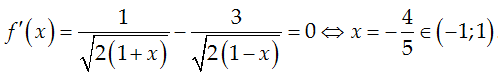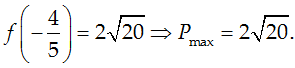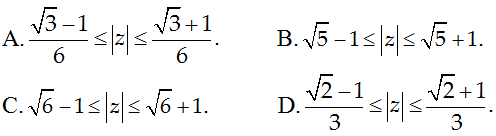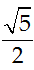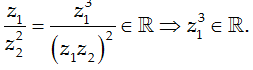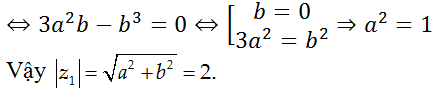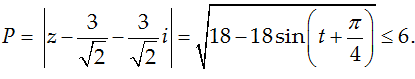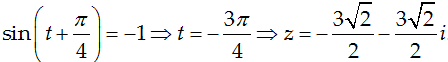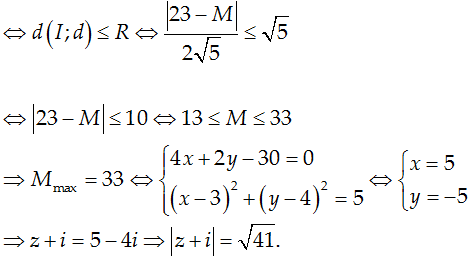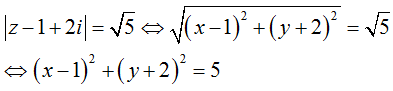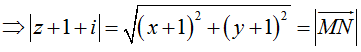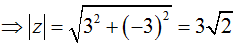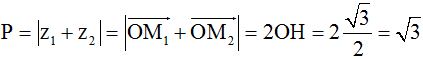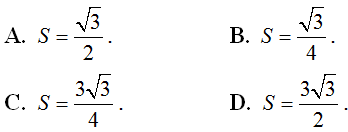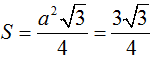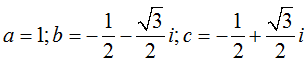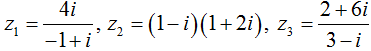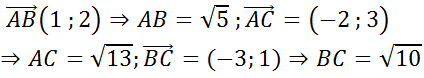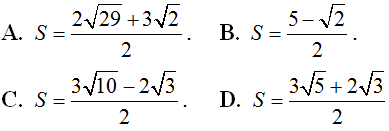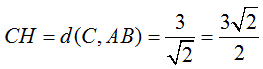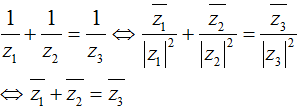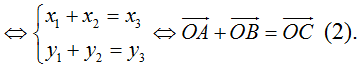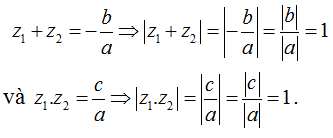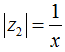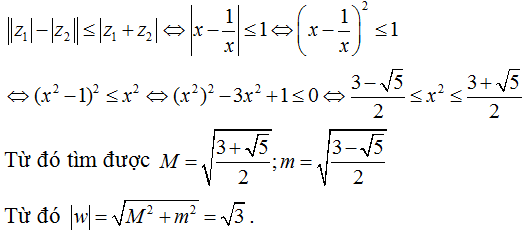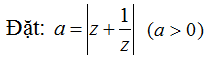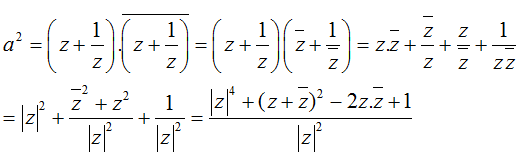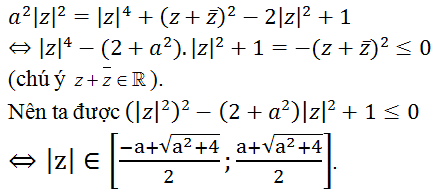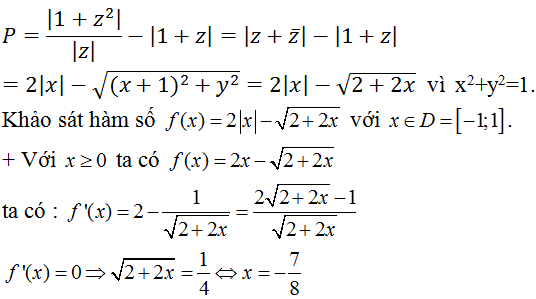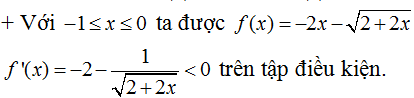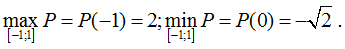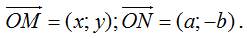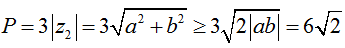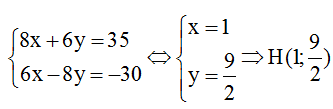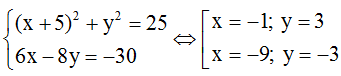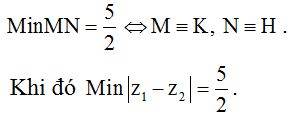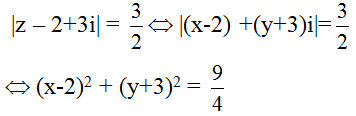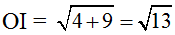Bài tập số phức nâng cao, hay và khó chọn lọc - Toán lớp 12
Bài tập số phức nâng cao, hay và khó chọn lọc
Với Bài tập số phức nâng cao, hay và khó chọn lọc Toán lớp 12 tổng hợp các dạng bài tập, trên 50 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
20 bài tập Số phức
Câu 1: Cho số phức z thỏa mãn điều kiện |z - 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích:
A. S = 9π B. S = 12π. C. S = 16π. D.S = 25π.
Hướng dẫn:
Ta có:
<=> |w - 1 + i - 6 + 8i| ≤ 4 <=> |w - 7 + 9i| ≤ 4 (1)
Giả sử w = x + yi, khi đó (1) <=> (x - 7)2 + (y + 9)2 ≤ 16
Suy ra tập hợp điểm biểu diễn số phức w là hình tròn tâm I(7; -9), bán kính r = 4
Vậy diện tích cần tìm là S = π.42 = 16π
Chọn C.
Câu 2: Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức
A.5 B.4 C.6 D.8
Hướng dẫn:
Ta có:
Khi z = i thì A = 6
Chọn C.
Câu 3. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất max M và giá trị nhỏ nhất min M của biểu thức M = |z2 + z + 1| + |z3 + 1|
A. max M = 5; min M = 1 B. max M = 5; min M = 2
C. max M = 4; min M = 1 D.max M = 4; min M = 2
Hướng dẫn:
Ta có: M ≤ |z|2 + |z| + 1 + |z|3 + 1 = 5 ,
khi z = 1 thì M = 5 nên max M = 5
Mặt khác:
khi z = -1 thì M = 1 nên min M = 1
Chọn A.
Câu 4. Cho số phức z thỏa |z| ≥ 2 . Tìm tích của giá trị lớn nhất và nhỏ nhất của biểu thức:
Hướng dẫn:
Ta có:
Mặt khác:
Vậy, giá trị nhỏ nhất của P là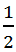 
, xảy ra khi z = -2i
giá trị lớn nhất của P bằng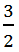 
xảy ra khi z = 2i
Chọn A.
Câu 5. Cho số phức z thỏa mãn |z| = 1. Tìm giá trị lớn nhất của biểu thức P = |1 + z| + 3|1 - z|
Hướng dẫn:
Gọi z = x + yi.
Ta có:
=> y2 = 1 - x2 => x ∈ [-1; 1]
Ta có:
P = |1 + z| + 3|1 - z|
Xét hàm số:
Hàm số liên tục trên [-1; 1] và với x ∈ (-1; 1) ta có:
Ta có:
f(1) = 2; f(-1) = 6;
Chọn D.
Câu 6 . Cho số phức z thỏa mãn điều kiện |z2 + 4| = 2|z|. Khẳng định nào sau đây là đúng?
Hướng dẫn:
Áp dụng bất đẳng thức |u| + |v| ≥ | u + v|, ta được:
2|z| + |-4| = |z2 + 4| + |-4| ≥ |z|2 => |z|2 - 2|z| - 4 ≤ 0 => |z| ≤ √5 + 1.
2|z| + |z|2 = |z2 + 4| + |-z2| ≥ 4 => |z|2 + 2|z| - 4 ≥ 0 => |z| ≥ √5 - 1
Vậy |z| nhỏ nhất là √5 - 1 khi z = -1 + i√5 và |z| lớn nhất là √5 + 1 khi z = 1 + i√5
Chọn B.
Câu 7. Cho z1; z2 là hai số phức liên hợp của nhau và thỏa mãn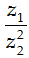 
∈ R và |z1 - z2| = 2√3. Tính môđun của số phức z1.
A. |z1| = √5
B. |z1| = 3
C. |z1| = 2
D. |z1| = 
Hướng dẫn:
Gọi z1 = a + bi; z2 = a - bi.
Không mất tính tổng quát ta coi b ≥ 0
Do |z1 - z2| = 2√3 => |2bi| = 2√3 => b = √3
Do z1; z2 là hai số phức liên hợp của nhau nên z1; z2 ∈ R, mà:
Ta có:
(z1)3 = (a + bi)3 = (a3 - 3ab2) + (3a2b - b3)i ∈ R
Chọn C.
Câu 8. Gọi z = x + yi là số phức thỏa mãn hai điều kiện: |z - 2|2 + |z + 2|2 = 26 và
đạt giá trị lớn nhất. Tính tích xy.
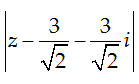
Hướng dẫn:
Đặt z = x + yi Thay vào điều kiện thứ nhất, ta được x2 + y2 = 36
Đặt x = 3.cost; y = 3sint. Thay vào điều kiện thứ hai, ta có:
Dấu bằng xảy ra khi:
Chọn D.
Câu 9. Biết số phức z thỏa mãn đồng thời hai điều kiện |z - 3 - 4i| = √5 và biểu thức M = |z + 2|2 - |z - i|2 đạt giá trị lớn nhất. Tính môđun của số phức z + i.
A. |z + i| = 2√41
B. |z + i| = 3√5
C. |z + i| = 5√2
D. |z + i| = √41
Hướng dẫn:
Gọi z = x + yi.
Ta có: |z - 3 - 4i| = √5 <=> (C): (x - 3)2 + (y - 4)2 = 5, tâm I(3; 4) và R = √5
Mặt khác:
M = |z + 2|2 - |z - i|2 = (x + 2)2 + y2 - [(x2) + (y - 1)2] = 4x + 2y + 3
<=> d: 4x + 4y + 3 - M = 0
Do số phức z thỏa mãn đồng thời hai điều kiện nên d và (C) có điểm chung
Chọn D.
Câu 10. Cho số phức z thỏa mãn điều kiện: |z - 1 + 2i| = √5 và w = z + 1 + i có môđun lớn nhất. Số phức z có môđun bằng:
A. 2√5 B. 3√2
C. √6 D. 5√2
Hướng dẫn:
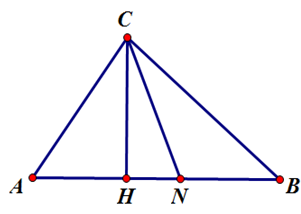
Gọi z = x + y; khi đó: z - 1 + 2i = (x - 1) + (y + 2)i
Ta có:
Suy ra tập hợp điểm M(x; y) biểu diễn số phức z thuộc đường tròn (C) tâm I(1; -2) bán kính R = √5 như hình vẽ:
Dễ thấy O ∈ (C), N(-; -1) ∈ (C),
Theo đề ta có: M(x; y) ∈ (C) là điểm biểu diễn cho số phức z thỏa mãn: w = z + 1 + i = x + yi + 1 + i = (x + 1) + (y + 1)i
Suy ra |z + 1 + i|đạt giá trị lớn nhất khi MN lớn nhất
Mà M, N ∈ (C) nên MN lớn nhất khi MN là đường kính đường tròn (C)
Khi và chỉ khi I là trung điểm MN => M(3; 3) => z = 3 - 3i
Chọn B
Câu 11: Cho hai số phức z1; z2 có điểm biểu diễn lần lượt là M1; M2 cùng thuộc đường tròn có phương trình x2 + y2 = 1 và |z1 - z2| = 1. Tính giá trị biểu thức P = |z1 + z2|
Hướng dẫn:
M1; M2 đường tròn (T) có tâm O(0; 0) và bán kính R = 1
Ta có |z1 - z2| = 1 hay M1M2 = 1.tam giác OM1M2 là tam giác đều cạnh bằng 1
Suy ra:
Chọn D.
Câu 12. Cho các số phức a; b;c thỏa mãn a + b + c = 0 và |a| = |b| = |c| = 1. Gọi A; B: C lần lượt là điểm biểu diễn cho các số phức a; b; c . Tính diện tích của tam giác ABC
Hướng dẫn:
Cách 1: (Tự luận)
+ Trước hết ta chứng minh tam giác ABC đều nội tiếp đường tròn bán kính bằng 1. Thực vậy: từ giả thiết |a| = |b| = |c| = 1. Nên A; B; C đều thuộc đường tròn (O;R = 1) .
+ Ta chứng minh tam giác ABC đều. Chú ý: |a - b| = AB
+ Từ a + b + c = 0 nên a = -b -c => |b + c| = 1 và |c + a| = |a + b| = 1 .
Mặt khác theo hằng đẳng thức hình bình hành ta có |a + b|2 + |a - b|2 = 2(|a|2 + |b|2) nên ta có được |a - b|2 = 2.2 - 1 = 3 => |a - b| = √3 => AB = √3 .
Tương tự ta tính được BC = CA = √3 . Do đó tam giác ABC đều với cạnh bằng √3 nên có diện tích bằng
Cách 2: Chuẩn hóa bằng các số phức:
Khi đó ta dễ thấy các số phức trên thỏa mãn các điều kiện của bài toán.
từ đó ta tìm được diện tích của tam giác ABC.
Chọn C.
Câu 13. Gọi A, B, C lần lượt là điểm biểu diễn các số phức
Khi đó, mệnh đề nào dưới đây là đúng.
A. A; B; Cthẳng hàng. B. Tam giác ABC là tam giác tù.
C. ΔABC là tam giác đều. D. Tam giác ABC là tam giác vuông cân.
Hướng dẫn:
Ta có z1 = 2 - i; z2 = 3 + i; z3 = 2i.
Từ trên ta được A( 2; -1); B(3; 1); C(0; 2).
Ta được:
- Do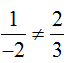 
nên ba điểm A; B; C không thẳng hàng từ đó ta được tam giác ABC.
- Dễ thấy tam giác ABC không phải là tam giác đều và cũng không phải tam giác vuông.
Vậy tam giác ABC là tam giác tù.
Chọn B.
Câu 14. Cho số phức z thỏa mãn |z - 1 + 2i| + |z + 2 - i| = 3√2. Gọi M; m lần lượt là giá trị lớn nhất và nhỏ nhất của biểu thức P = |z - 3 + i|. Giá trị của tổng S = M + m là:
Hướng dẫn:
+ Trước hết ta có mệnh đề quen thuộc: Nếu z; z’ lần lượt có điểm biểu diễn là A; A’ thì |z' - z| = A'A .
+ Xét các số phức z1 = 1 - 2i; z2 = -2 + i; z3 = 3 - i và z = x + yi lần lượt có điểm biểu diễn là A; B; C và N.
Khi đó ta có giả thiết là NA + NB = 3√2 (1) với AB = 3√2 (2).
Từ (1) và (2) ta được N thuộc đoạn thẳng AB.
Yêu cầu bài toán là tìm min hoặc max của biểu thức S = NC với ABC là 3 đỉnh của tam giác.
Khi đó minP = NC; maxP = max{CA,CB} .
+ Ta có đường thẳng AB: x + y + 1 = 0 nên
+ CA = √5;CB = √29 suy ra max P = √29.
Chọn A.
Câu 15. Cho 3 số phức z1; z2; z3 phân biệt thỏa mãn |z1| = |z2| = |z3| = 3 và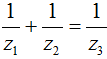 
Biết rằng các điểm biểu diễn cho các số phức z1; z2; z3 lần lượt là A; B; C. Tính số đo góc ∠ACB
A. 60o
B. 90o
C. 150o
D. 120o
Hướng dẫn:
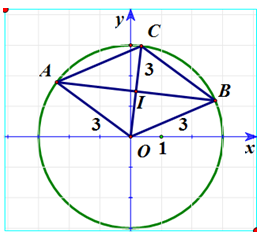
Giả sử zk = xk + yk, khi đó điểm A(x1; y1); B( x2; y2); C(x3; y3) lần lượt là điểm biểu diễn cho các số phức z1; z2; z3 trên mặt phẳng tọa độ Oxy.
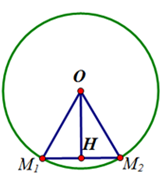
+ Từ giả thiết |z1| = |z2| = |z3| = 3 => OA = OB = OC = 3nên A; B; C đều thuộc đường tròn tâm O, bán kính R = 3.
(vì |z1| = |z2| = |z3| = 3 ) hay x1 - y1.i + x2 - y2.i = x3 - y3i.
+ Vì OA = OB = 3 và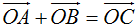 
nên OACB là hình thoi với một đường chéo OC = 3.
+ Từ trên suy ra tam giác OAC; OBC đều cạnh bằng 3 nên ∠ACB = 120o
Chọn D.
Câu 16. Cho các số phức a; b; c; z thỏa mãn az2 + bz + c = 0 và |a| = |b| = |c| > 0 . Kí hiệu M = max|z|, m = min|z|. Tính mô đun của số phức w = M - mi.
A. |w| = √3 B. |w| = 1 C. |w| = 2√3 D. |w| = 2
Hướng dẫn:
Ta thấy phương trình az2 + bz + c = 0 trên tập số phức luôn có hai nghiệm phân biệt hoặc trùng nhau z1; z2.
Theo định lý vi – ét ta có:
Đặt |z1| = x > 0; x ∈ R , khi đó ta có:
Từ bất đẳng thức |z1| + |z2| ≥ |z1 + z2| nên ba số |z1|, |z2|, |z1 + z2| là 3 cạnh của một tam giác (có thể suy biến thành đoạn thẳng).
Áp dụng bất đẳng thức tam giác ngược ta được:
Chọn A.
Câu 17. Cho số phức z thỏa mãn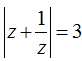 
. Tổng giá trị lớn nhất, nhỏ nhất của |z| là:
A. 3 B. √5 C. √13 D. 5
Hướng dẫn:
Với giả thiết ta có:
Từ đó ta được:
Từ đó bằng cách thay a cụ thể ta được đáp án C.
Câu 18. Cho số phức z thỏa mãn |z| = 1 Tìm tổng giá trị lớn nhất, nhỏ nhất của biểu thức P với P = |1 + z22| - |1 + z| ?
A. 2 + √2 B. 1 + 2√2 C. -1 + 2√2 D. 2 - √2
Hướng dẫn:
Ta có:
nên ta có maxP = P(1) = 0; minP = P(0) = -√2.
Hàm số nghịch biến trên .
Từ đó ta được max P = P(-1) = 2; minP = P(0) = -√2.
+ Từ trên ta được:
Chọn A.
Câu 19. Cho hai số phức z1; z2 thỏa mãn |z1|z1 = 4|z2|z2 và nếu gọi M, N là điểm biểu diễn z1;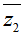 
trong mặt phẳng tọa độ thì tam giác giác MON có diện tích là 8. Tìm giá trị nhỏ nhất của |z1 + z2|
A. 3√3 B.8 C. 6√2 D.5
Hướng dẫn:
Giải theo tự luận
+ Từ giả thiết |z1|z1 = 4|z2|z2, suy ra |z1| = 2|z2| và ta được z1 = 2z2.
+ Giả sử z1 = x + yi; z2 = a + bi. Ta được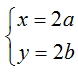 
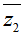
và M(x; y); N(a; -b); N’(a; b) lần lượt là các điểm biểu diễn cho các số phức z1, và z2.
Ta có:
Từ diện tích của tam giác OMN bằng 8 nên |bx + ay| = 16 hay |ab| = 4 (1).
Ta có:
Dấu bằng diễn ra khi và chỉ khi :
Chọn C.
Câu 20. Cho hai số phức z1; z2 thỏa mãn |z1 + 5| = 5, |z2 + 1 - 3i| = |z2 - 3 - 6i|. Tìm giá trị nhỏ nhất của |z1 - z2|
Hướng dẫn:
Giả sử M(a; b) là điểm biểu diễn của số phức z1 = a + bi, N(c; d) là điểm biểu diễn của số phức z2 = c + di
Ta có: |z1 + 5| = 5 <=> (z1 + 5)2 + b2 = 25
Vậy M thuộc đường tròn (C): (x + 5)2 + y2 = 25
|z2 + 1 - 3i| = |z2 - 3 - 6i| <=> 8c + 6d = 35
Vậy N thuộc đường thẳng Δ 8x + 6y = 35
Dễ thấy đường thẳng Δ không cắt (C) và |z1 - z2| = M .
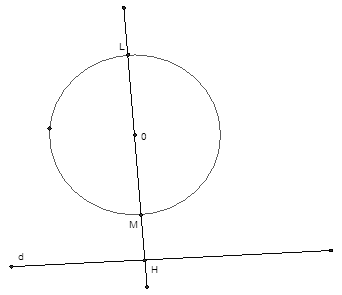
Bài toán trở thành: Trong mặt phẳng Oxy cho đường tròn (C) và đường thẳng 8x + 6y = 35. Tìm giá trị nhỏ nhất của MN, biết M chạy trên (C) , N chạy trên đường thẳng Δ .
Gọi d là đường thẳng qua I và vuông góc với Δ .
PT đường thẳng d là 6x - 8y = -30.
Gọi H là giao điểm của d và Δ . Tọa độ điểm H là nghiệm của hệ
Gọi K, L là giao điểm của d với đường tròn (C). Tọa độ K, L là nghiệm của hệ
Vậy K(-1; 3), L(-9; -3)
Tính trực tiếp HK, HL. Suy ra
Câu 21. Trong các số phức z thoả mãn điều kiện: |z – 2 + 3i| =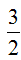 
. Tìm số phức z có môđun nhỏ nhất.
Hướng dẫn:
Giả sử z = x + yi, khi đó:
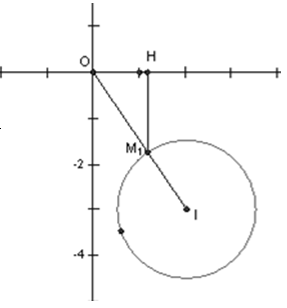
=> Tập hợp điểm M thoả mãn điều kiện đã cho là đường tròn tâm I(2; -3) và bán kính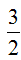
Môđun của z đạt giá trị nhỏ nhất khi và chỉ khi M thuộc đường tròn và gần O nhất
=> M trùng với M1 là giao của đường thẳng OI với đường tròn.
Ta có:
Kẻ M1H ⊥ Ox. Theo định lý Talet ta có:
