Top 50 bài tập Số phức (mới nhất)

Câu 1:

Cho i là đơn vị ảo. Với $x,y\in \mathrm{ℝ}$ thì x - 1 + (y + 3)i  là số thuần ảo khi và chỉ khi

Xem lời giải »

Câu 2:

Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z - i + 1| = |z + i - 2| là đường thẳng có phương trình

Xem lời giải »

Câu 3:

Cho i là đơn vị ảo. Cho $m\in \mathrm{ℝ}$. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn hình học số phức z = mi có tọa độ là

Xem lời giải »

Câu 4:

Cho i là đơn vị ảo. Giá trị của biểu thức $z = {\left(i^5+i^4+i^3+i^2+i+1\right)}^{40}$ là

Xem lời giải »

Câu 5:

Gọi z₁, z₂ là các nghiệm của phương trình $z^2 -2z + 6 = 0$. Tính $P = {z_1}^{4 } + {z_2}^4$

B. 8

D. -8

Xem lời giải »

Câu 6:

Cho số phức $z= \frac{1-i}{1+i}$. Phần thực của số phức $z^{2017}$ là

A. 0

B. 1

C. 2

D. 3

Xem lời giải »

Câu 7:

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện $\left|z +1\right| \le 2$ là

D. Hình tròn tâm I(-1; 0), bán kính R = 2

Xem lời giải »

Câu 8:

Cho số phức z thỏa mãn điều kiện $\left(z +1\right)\left(i-\overline{z}\right)$ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng

Xem lời giải »

Câu 9:

Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn $\left|z-1-i\right|=1$. Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?

Xem lời giải »

Câu 10:

Phần thực của số phức $w= 1+ \left(1+i\right)+{\left(1+i\right)}^2+{\left(1+i\right)}^3+...+{\left(1+i\right)}^{1999}$  bằng

 A. 1

B. 0

Xem lời giải »

Câu 11:

Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức -2, 4i,  x+2i. Với giá trị nào của x thì A, B, M thẳng hàng.

Xem lời giải »

Câu 12:

Số phức z thỏa mãn $(2 + 3i)\overline{z} + \left(1-i\right)z = 3+5i$ Tìm môđun của số phức z.

A. 11

C. 9

Xem lời giải »

Câu 13:

Cho z = 1 + 2i, số phức $z^{,}$ đối xứng với số phức z qua gốc tọa độ O (0;0) là

Xem lời giải »

Câu 14:

Cho số phức z = a+bi ; a,b $\in \mathrm{ℝ}$. Nhận xét nào sau đây luôn đúng?

Xem lời giải »

Câu 15:

Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện $\left|zi-\left(1-2i\right)\right|=4$ là

Xem lời giải »

Câu 16:

Số phức liên hợp của số phức $z = \left(1+i\right)\left(4-3i\right)$ là

Xem lời giải »

Câu 1:

Cho số phức $z={(1+i)}^5$. Điểm biểu diễn số phức z nằm trong góc phần tư nào của hệ tọa độ vuông góc của mặt phẳng phức?

A. Góc phân tư thứ IV

B. Góc phân tư thứ I

C. Góc phân tư thứ II

D. Góc phân tư thứ III

Xem lời giải »

Câu 2:

Số đối của số phức z = -1 + 2i là

Xem lời giải »

Câu 3:

Cho số phức z thỏa mãn $\left|z-1\right|=\left|z+2i+1\right|$. Biết tập hợp các điểm biểu thị cho z là một đường thẳng. Phương trình đường thẳng đó là

A. x – y + 1 = 0

B. x + y + 1 = 0

C. 4x – 4y + 3 = 0

D. 4x + 4y + 3 = 0

Xem lời giải »

Câu 4:

Tìm số phức z biết rằng điểm biểu diễn của z nằm trên đường tròn tâm O bán kính bằng 1 và nằm trên đường thẳng x + y = $\sqrt{2}$ 

Xem lời giải »

Câu 5:

Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức $z_1=-i$; $z_2=2+i$; $z_3=-1+i$.  Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành

Xem lời giải »

Câu 1:

Cho số phức z = 2 – 2i. Tìm khẳng định sai. 

A. Phần thực của z là: 2.

B. Phần ảo của z là: -2.

C. Số phức liên hợp của z là $\overline{z} = -2 + 2i.$

D. Môđun của z là $\left|z\right|=\sqrt{2^2+{\left(-2\right)}^2}=2\sqrt{2}$

Xem lời giải »

Câu 2:

Cho số phức z = -1 + 3i. Phần thực, phần ảo của $\overline{z}$ là

A. -1 và 3    

B. -1 và -3    

C. 1 và -3    

D. -1 và -3i

Xem lời giải »

Câu 3:

Môđun của số phức z thỏa mãn $\overline{z} = 8 - 6i$ là

A. 2

B. 10

C. 14

D .7

Xem lời giải »

Câu 4:

Tìm các số thực x, y sao cho$(x – 2y) + (x + y + 4).i = (2x + y) + 2yi.$

A. x = 3, y = 1     

B. x = 3, y = -1

C. x = -3, y = -1     

D. x = -3, y = 1

Xem lời giải »

Câu 5:

Hai số phức $z_1=x-2i,{ z}_2=2+yi$ (x, y ∈ R) là liên hợp của nhau khi

A. x = 2, y = -2   

B. x = -2, y = -2    

C. x = 2, y = 2     

D. x = -2, y = 2

Xem lời giải »

Câu 6:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = |1 + i| là

A. Hai điểm     

B. Hai đường thẳng

C. Đường tròn bán kính R=2 

D. Đường tròn bán kính $R= \sqrt{2}$

Xem lời giải »

Câu 7:

Phần thực của số phức z = -i là

A. -1

B. 1

C. 0

D. -i

Xem lời giải »

Câu 8:

Phần ảo của số phức z = -1 là

A. -i

B. 1

C. -1

D. 0

Xem lời giải »

Câu 9:

Số phức liên hợp của số phức z = 1 + i là

A. 1-i

B. -1-i

C. -1+i

D. 1+i

Xem lời giải »

Câu 10:

Cho z = 2i -1. Phần thực và phần ảo của $\overline{z}$ là

A. 2 và 1    

B. -1 và -2    

C. 1 và 2i   

D. -1 và -2i

Xem lời giải »

Câu 11:

Môđun của số phức z = -3 + 4i là

A. 5

B. -3

C. 4

D. 7

Xem lời giải »

Câu 12:

Môđun của số phức $z = 2 -\sqrt{ 3}i$ là

A. $\sqrt{7}$

B. $2+\sqrt{3}$

C. $2-\sqrt{3}$

D. 7

Xem lời giải »

Câu 13:

Số phức z = 1 - 2i có điểm biểu diễn là 

A. M (1; 2)   

B. M (1; -2)   

C. M (-1; 2)   

D. M (-1; -2)

Xem lời giải »

Câu 14:

Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và $\overline{z }= 1 - i$ đối xứng nhau qua

A. Trục tung    

B. Trục hoành   

C. Gốc tọa độ   

D. Điểm I (1; -1)

Xem lời giải »

Câu 15:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là

A. Hai đường thẳng 

B. Đường tròn bán kính bằng 2

C. Đường tròn bán kính bằng 4

D. Hình tròn bán kính bằng 2

Xem lời giải »

Câu 16:

Gọi A, B là các điểm biểu diễn của các số phức $z_1 = -1 + 2i, z_2 = 2 + 3i .$ Khi đó, độ dài đoạn thẳng AB là

A. $\sqrt{26}$

B. $\sqrt{5}+\sqrt{13}$

C. $\sqrt{10}$

D. 10

Xem lời giải »

Câu 1:

Số phức z = a + bi có phần thực là:

A. a

B. b

C. i

D. z

Xem lời giải »

Câu 2:

Kí hiệu a, b là phần thực và phần ảo của số phức $3-2\sqrt{2}\mathrm{i}$. Tính P = ab.

A. $\mathrm{P}=6\sqrt{2}\mathrm{i}$

B. $\mathrm{P}=6\sqrt{2}$

C. $\mathrm{P}=-6\sqrt{2}\mathrm{i}$

D. $\mathrm{P}=-6\sqrt{2}$

Xem lời giải »

Câu 3:

Số phức z = a + bi là số thực nếu:

A. a = 0

B. b = 0

C. i = 0

D. ab = 0

Xem lời giải »

Câu 4:

Số phức $\mathrm{z}=\sqrt{2}\mathrm{i}-1$ có phần thực là:

A. -1

B. 2

C. 1

D. $\sqrt{2}$

Xem lời giải »

Câu 5:

Số phức nào dưới đây là số thuần ảo?

A. $\mathrm{z}=-2+3\mathrm{i}$

B. $\mathrm{z}=3\mathrm{i}$

C. $\mathrm{z}=-2$

D. $\mathrm{z}=\sqrt{3}+1$

Xem lời giải »

Câu 6:

Hai số phức $\mathrm{z}=\mathrm{a}+\mathrm{bi},\mathrm{z}\text{'}=\mathrm{a}+\mathrm{b}\text{'}\mathrm{i}$ bằng nhau nếu:

A. a = b'

B. a = b

C. b = b'

D. a = -b

Xem lời giải »

Câu 7:

Cho hai số phức ${\mathrm{z}}_1=\mathrm{a}+\mathrm{bi} \left(\mathrm{a},\mathrm{b}\in \mathrm{R}\right)$ và ${\mathrm{z}}_2=2017-2018\mathrm{i}$. Biết ${\mathrm{z}}_1={\mathrm{z}}_2$, tính tổng $\mathrm{S}=\mathrm{a}+2\mathrm{b}$

A. S = -1

B. S = 4035

C. S= -2019

D. S = -2016

Xem lời giải »

Câu 8:

Số phức liên hợp của số phức $\mathrm{z}=\mathrm{a}-\mathrm{bi}$ là:

A. $\mathrm{a}-\mathrm{bi}$

B. $\mathrm{a}+\mathrm{bi}$

C. $\mathrm{b}-\mathrm{ai}$

D. $\mathrm{b}+\mathrm{ai}$

Xem lời giải »

Câu 9:

Cho số phức $\mathrm{z}=3+2\mathrm{i}$. Tìm phần thực và phần ảo của số phức $\overline{\mathrm{z}}$

A. Phần thực bằng – 3 và phần ảo bằng – 2i

B. Phần thực bằng 3 và phần ảo bằng – 2

C. Phần thực bằng 3 và phần ảo bằng 2i

D. Phần thực bằng 3 và phần ảo bằng 2

Xem lời giải »

Câu 10:

Số phức liên hợp của số phức $\mathrm{z}=3\mathrm{i}+2$ là:

A. $\overline{\mathrm{z}}=3\mathrm{i}-2$

B. $\overline{\mathrm{z}}=-3\mathrm{i}-2$

C. $\overline{\mathrm{z}}=3\mathrm{i}+2$

D. $\overline{\mathrm{z}}=2-3\mathrm{i}$

Xem lời giải »

Câu 11:

Chọn mệnh đề đúng:

A. $\overline{\mathrm{z}}=\mathrm{z}$

B. $\left|\overline{\mathrm{z}}\right|=\left|\mathrm{z}\right|$

C. $\left|\overline{\mathrm{z}}\right|+\left|\mathrm{z}\right|=0$

D. $\left|\overline{\mathrm{z}}.\mathrm{z}\right|=0$

Xem lời giải »

Câu 12:

Gọi M, N lần lượt là các điểm biểu diễn số phức $\mathrm{z}=\mathrm{a}+\mathrm{bi}$ và $\mathrm{z}\text{'}=\mathrm{a}\text{'}+\mathrm{b}\text{'}\mathrm{i}$. Chọn câu đúng:

A. $\mathrm{M}\left(\mathrm{a};\mathrm{a}\text{'}\right)$

B. $\mathrm{N}\left(\mathrm{b};\mathrm{b}\text{'}\right)$

C. $\mathrm{M}\left(\mathrm{a};\mathrm{b}\right)$

D. $\mathrm{N}\left(\mathrm{b}\text{'};\mathrm{a}\text{'}\right)$

Xem lời giải »

Câu 13:

Tìm điểm M biểu diễn số phức $\mathrm{z}=\mathrm{i}-2$

A. $\mathrm{M}\left(1;-2\right)$

B. $\mathrm{M}\left(2;-1\right)$

C. $\mathrm{M}\left(-2;1\right)$

D. $\mathrm{M}\left(2;1\right)$

Xem lời giải »

Câu 14:

Trong mặt phẳng tọa độ (hình vẽ bên). Số phức $\mathrm{z}=3-4\mathrm{i}$ được biểu diễn bởi điểm nào trong các điểm A, B, C, D?

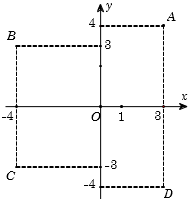
A. Điểm A

B. Điểm B

C. Điểm C

D. Điểm D

Xem lời giải »

Câu 15:

Điểm nào trong hình vẽ bên là điểm biểu diễn số phức $\mathrm{z}=-1+2\mathrm{i}$?

A. N

B. P

C. M

D. Q

Xem lời giải »

Câu 1:

Số phức $\mathrm{z}=-1-\mathrm{m}+\mathrm{mi}$ là số thực nếu:

A. m = 1

B. m = 0

C. m = -1

D. Không tồn tại

Xem lời giải »

Câu 2:

Biết rằng có duy nhất một cặp số thực (x; y) thỏa mãn $\left(\mathrm{x}+\mathrm{y}\right)+\left(\mathrm{x}-\mathrm{y}\right)\mathrm{i}=5+3\mathrm{i}$

A. S = 5

B. S = 3

C. S = 4

D. S = 6

Xem lời giải »

Câu 3:

Cho hai số phức $\mathrm{z}=\left(2\mathrm{x}+3\right)+\left(3\mathrm{y}-1\right)\mathrm{i}$ và $\mathrm{z}\text{'}=3\mathrm{x}+\left(\mathrm{y}+1\right)\mathrm{i}$. Khi $\mathrm{z}=\mathrm{z}\text{'}$, chọn khẳng định đúng trong các khẳng định sau:

A. $\mathrm{x}=-\frac{5}{3};\mathrm{y}=0$

B. $\mathrm{x}=-\frac{5}{3};\mathrm{y}=\frac{4}{3}$

C. $\text{x=3,y=1}$

D. $\text{x=1,y=3}$

Xem lời giải »

Câu 4:

Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức $3-2\sqrt{2}\mathrm{i}$. Tìm a, b

A. $\mathrm{a}=3,\mathrm{b}=2$

B. $\mathrm{a}=3,\mathrm{b}=2\sqrt{2}$

C. $\mathrm{a}=3,\mathrm{b}=\sqrt{2}$

D. $\mathrm{a}=3,\mathrm{b}=-2\sqrt{2}$

Xem lời giải »

Câu 5:

Cho số phức $\mathrm{z}=3-2\mathrm{i}$. Tìm phần thực và phần ảo của số phức $\overline{\mathrm{z}}$

A. Phần thực bằng – 3 và phần ảo bằng – 2i

B. Phần thực bằng – 3 và phần ảo bằng – 2

C. Phần thực bằng 3 và phần ảo bằng 2i

D. Phần thực bằng 3 và phần ảo bằng 2

Xem lời giải »

Câu 6:

Cho ${\mathrm{z}}_1=2+\mathrm{i};{\mathrm{z}}_2=1-3\mathrm{i}$. Tính $\mathrm{A}={\left|{\mathrm{z}}_1\right|}^2+{\left|{\mathrm{z}}_2\right|}^2$

A. 2

B. 3

C. 4

D. 15

Xem lời giải »

Câu 7:

Cho hai số phức ${\mathrm{z}}_1=-1+2\mathrm{i};{\mathrm{z}}_2=1+2\mathrm{i}$. Tính $\mathrm{T}={\left|{\mathrm{z}}_1\right|}^2+{\left|{\mathrm{z}}_2\right|}^2$

A. T = $2\sqrt{5}$

B. T = 4

C. T = 10

D. T = 7

Xem lời giải »

Câu 8:

Cho số phức $\mathrm{z}=3-4\mathrm{i}$. Mô đun của z bằng:

A. 7

B. 1

C. 12

D. 5

Xem lời giải »

Câu 9:

Trên mặt phẳng tọa độ, điểm M là điểm biểu diễn của số phức z (như hình bên). Điểm nào trong hình vẽ là điểm biểu diễn của số phức 2z?

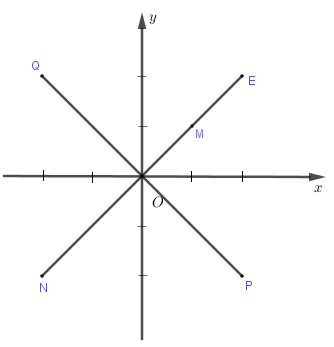
A. Điểm N

B. Điểm Q

C. Điểm E

D. Điểm P

Xem lời giải »

Câu 10:

Số phức z thỏa mãn $\left|\mathrm{z}\right|+\mathrm{z}=0$. Khi đó:

A. z là số thuần ảo.

B. Mô đun của z bằng 1.

C. z là số thực nhỏ hơn hoặc bằng 0.

D. Phần thực của z là số âm.

Xem lời giải »

Câu 11:

Gọi A và B lần lượt là điểm biểu diễn của số phức ${\mathrm{z}}_1=3-2\mathrm{i}$ và ${\mathrm{z}}_2=1+4\mathrm{i}$. Trung điểm của đoạn thẳng AB có tọa độ là

A. $\left(1;-3\right)$

B. $\left(2;3\right)$

C. $\left(2;1\right)$

D. $\left(4;2\right)$

Xem lời giải »

Câu 12:

Biết rằng điểm biểu diễn số phức z là điểm M ở hình bên dưới. Modun của z bằng

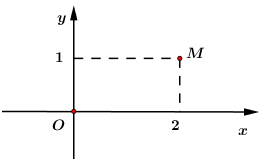
A. 5

B. $\sqrt{5}$

C. $\sqrt{3}$

D. 3

Xem lời giải »

Câu 13:

Trên mặt phẳng tọa độ điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Khẳng định nào sau đây là đúng?

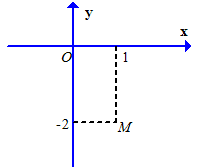
A. $\overline{\mathrm{z}}=1-2\mathrm{i}$

B. $\left|\mathrm{z}\right|=\sqrt{5}$

C. $\mathrm{z}=1+2\mathrm{i}$

D. $\mathrm{z}=-2+\mathrm{i}$

Xem lời giải »

Câu 14:

Gọi M là N lần lượt là điểm biểu diễn của các số phức ${\mathrm{z}}_1,{\mathrm{z}}_2$ khác 0. Khi đó khẳng định nào sau đây sai?

A. $\left|{\mathrm{z}}_2\right|=\mathrm{ON}$

B. $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\mathrm{MN}$

C. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=\mathrm{MN}$

D. $\left|{\mathrm{z}}_2\right|=\mathrm{OM}$

Xem lời giải »

Câu 15:

Tìm số phức có phần thực bằng 12 và mô đun bằng 13:

A. $5\pm 12\mathrm{i}$

B. $12+5\mathrm{i}$

C. $12\pm 5\mathrm{i}$

D. $12\pm \mathrm{i}$

Xem lời giải »

Câu 1:

Gọi A là điểm biểu diễn số phức z = -1 + 6i và B là điểm biểu diễn của số phức z' = -1 - 6i. Mệnh đề nào sau đây là đúng?

A. Hai điểm A và B đối xứng với nhau qua trục hoành.

B. Hai điểm A và B đối xứng nhau qua trục tung

C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O

D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.

Xem lời giải »

Câu 2:

Cho ba điểm A, B, C lần lượt biểu diễn các số phức sau ${\mathrm{z}}_1$= 1 + i, ${\mathrm{z}}_2$= ${\mathrm{z}}_1^2$, ${\mathrm{z}}_3$= m - i. Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.

A. m = -3.

B. m = 1.

C. m = -1.

D. m = 1.

Xem lời giải »

Câu 3:

Cho số phức z. Mệnh đề nào sau đây là đúng?

A. $\left|{\mathrm{z}}^2\right|=2\left|\mathrm{z}\right|$

B. $\left|{\mathrm{z}}^2\right|={\left|\mathrm{z}\right|}^2$

C. $\left|{\mathrm{z}}^2\right|=2{\left|\mathrm{z}\right|}^2$

D. $\left|{\mathrm{z}}^2\right|=\sqrt{{\left|\mathrm{z}\right|}^2}$

Xem lời giải »

Câu 4:

Gọi M là điểm biểu diễn của số phức z, biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng?

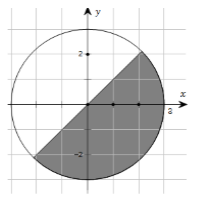
A. z có phần ảo không nhỏ hơn phần thực.

B. z có phần thực không nhỏ hơn phần ảo và có mô đun không lớn hơn 3.

C. z có phần thực bằng phần ảo.

D. z có mô đun lớn hơn 3.

Xem lời giải »

Câu 5:

Cho các số phức ${\mathrm{z}}_1=3-2\mathrm{i},{\mathrm{z}}_2=1+4\mathrm{i}$ và ${\mathrm{z}}_3=-1+\mathrm{i}$ có biểu diễn hình học trong mặt phẳng tọa độ Oxy lần lượt là các điểm A, B, C. Diện tích tam giác ABC bằng:

A. $2\sqrt{17}$

B. $12$

C. $4\sqrt{13}$

D. $9$

Xem lời giải »

Câu 6:

Cho ba điểm A, B, C lần lượt biểu diễn ba số phức ${\mathrm{z}}_1,{\mathrm{z}}_2,{\mathrm{z}}_3$ với ${\mathrm{z}}_3\ne {\mathrm{z}}_1$ và ${\mathrm{z}}_3\ne {\mathrm{z}}_2$. Biết $\left|{\mathrm{z}}_1\right|=\left|{\mathrm{z}}_2\right|=\left|{\mathrm{z}}_3\right|$ và ${\mathrm{z}}_1+{\mathrm{z}}_2=0$. Mệnh đề nào sau đây là đúng?

A. Tam giác ABC vuông tại C

B. Tam giác ABC đều

C. Tam giác ABC vuông cân tại C

D. Tam giác ABC cân tại C

Xem lời giải »

Câu 7:

Gọi A là điểm biểu diễn số phức z = 3 + 2i và B là điểm biểu diễn của số phức z’ = 2 + 3i. Mệnh đề nào sau đây là đúng?

A. Hai điểm A và B đối xứng với nhau qua trục hoành.

B. Hai điểm A và B đối xứng nhau qua trục tung

C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O

D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.

Xem lời giải »

Câu 8:

Trên mặt phẳng tọa độ Oxy, gọi M là điểm biểu diễn hình học của số phức z = -1 + 2i và $\mathrm{\alpha }$ là góc lượng giác có tia đầu Ox, tia cuối OM. Tính $\tan 2\mathrm{\alpha }$

A. $\frac{-3}{4}$

C. $\frac{-4}{3}$

D. $\frac{4}{3}$

Xem lời giải »

Câu 9:

Cho số phức z = m - 2 + $\left({\mathrm{m}}^2-1\right)\mathrm{i}$, m$\in \mathrm{ℝ}$. Gọi (C) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (C) và trục hoành bằng:

A. $\frac{4}{3}$

B. $\frac{32}{3}$

C. $\frac{8}{3}$

D. 1

Xem lời giải »

Câu 10:

Có bao nhiêu số phức z = a + bi với a, b tự nhiên thuộc đoạn [2;9] và tổng a + b chia hết cho 3?

A. 42

B. 27

C. 21

D. 18

Xem lời giải »

Câu 11:

Cho các số phức ${\mathrm{z}}_1$ = 3i; ${\mathrm{z}}_2$ = m - 2i. Số giá trị nguyên của m để $\left|{\mathrm{z}}_2\right|<\left|{\mathrm{z}}_1\right|$ là:

A. 2

B. 5

C. 4

D. 3

Xem lời giải »

Câu 12:

Tính mô đun của số phức $\mathrm{w}={\left(1-\mathrm{i}\right)}^2\mathrm{z}$. Biết số phức z có mô đun bằng m

A. $\left|\text{w}\right|=2\mathrm{m}$

B. $\left|\text{w}\right|=\mathrm{m}$

C. $\left|\text{w}\right|=\sqrt{2}\mathrm{m}$

D. $\left|\text{w}\right|=4\mathrm{m}$

Xem lời giải »

Câu 13:

Cho số phức z = $\left(\mathrm{m}+3\right)+\left({\mathrm{m}}^2-\mathrm{m}-6\right)\mathrm{i}$ với $\mathrm{m}\in \mathrm{R}$. Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng

A. $\frac{125}{6}$

B. $\frac{17}{6}$

C. $1$

D. $\frac{55}{6}$

Xem lời giải »

Câu 14:

Tìm các số thực x, y thỏa mãn đẳng thức 3x + y + 5xi = 2y - (x - y)i

A. $\left\{\begin{array}{c}\mathrm{x}=-\frac{1}{7}\\ \mathrm{y}=-\frac{4}{7}\end{array}\right.$

B. $\left\{\begin{array}{c}\mathrm{x}=\frac{4}{7}\\ \mathrm{y}=\frac{1}{7}\end{array}\right.$

C. $\left\{\begin{array}{c}\mathrm{x}=-\frac{4}{7}\\ \mathrm{y}=\frac{1}{7}\end{array}\right.$

D. $\left\{\begin{array}{c}\mathrm{x}=0\\ \mathrm{y}=0\end{array}\right.$

Xem lời giải »

Câu 15:

Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức ${\mathrm{z}}_1=3+2\mathrm{i};$${\mathrm{z}}_2=3-2\mathrm{i};$${\mathrm{z}}_3=-3-2\mathrm{i}$. Khẳng định nào sau đây là sai?

A. B và C đối xứng nhau qua trục tung.

B. Trọng tâm của tam giác ABC là $\mathrm{G}\left(1;\frac{2}{3}\right)$

C. A và B đối xứng với nhau qua trục hoành.

D. A, B, C nằm trên đường tròn tâm tại gốc tọa độ và bán kính bằng $\sqrt{13}$

Xem lời giải »

Câu 1:

Số phức liên hợp của z = 3 + 2i là:

A. $\overline{\mathrm{z}}=2-3\mathrm{i}$

B. $\overline{\mathrm{z}}=3-2\mathrm{i}$

C. $\overline{\mathrm{z}}=-2-3\mathrm{i}$

D. $\overline{\mathrm{z}}=-2-2\mathrm{i}$

Xem lời giải »

Câu 2:

Trong mặt phẳng tọa độ Oxy cho các điểm A, B như hình vẽ bên:

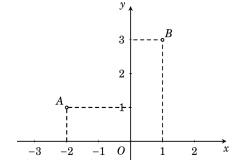
Trung điểm của đoạn thẳng AB biểu diễn số phức

A. $-1+2\mathrm{i}$

B. $-\frac{1}{2}+2\mathrm{i}$

C. $2-\mathrm{i}$

D. $2-\frac{1}{2}\mathrm{i}$

Xem lời giải »

Câu 3:

Trong các số phức ${\mathrm{z}}_1=-2\mathrm{i},{\mathrm{z}}_2=2-\mathrm{i},$${\mathrm{z}}_3=5\mathrm{i},{\mathrm{z}}_4=4$ có bao nhiêu số thuần ảo?

A. 4

B. 1

C. 3

D. 2

Xem lời giải »

Câu 4:

Cho số phức $\mathrm{z}=1+2\mathrm{i}$. Tìm mô đun của số phức $\overline{\mathrm{z}}$

A. $\sqrt{5}$

B. -1

C. $\sqrt{3}$

D. 3

Xem lời giải »

Câu 5:

Cho số phức $\mathrm{z}=4-3\mathrm{i}$. Khi đó $\left|\mathrm{z}\right|$ bằng:

A. 25

B. 5

C. 7

D. $\sqrt{7}$

Xem lời giải »

Câu 6:

Mô đun của số phức $\mathrm{z}=\sqrt{3}-\mathrm{i}$ bằng:

A. $\sqrt{2}$

B. 1

C. 4

D. 2

Xem lời giải »

Câu 7:

Giả sử M, N, P, Q được cho ở hình bên là điểm biểu diễn của các số phức ${\text{z}}_1,{\mathrm{z}}_2,{\mathrm{z}}_3,{\mathrm{z}}_4$ trên mặt phẳng tọa độ. Khẳng định nào sau đây là đúng?

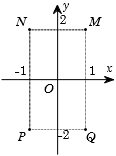
A. Điểm M là điểm biểu diễn số phức ${\mathrm{z}}_1=2+\mathrm{i}$

B. Điểm Q là điểm biểu diễn số phức ${\mathrm{z}}_4=-1+2\mathrm{i}$

C. Điểm N là điểm biểu diễn số phức ${\mathrm{z}}_2=2-\mathrm{i}$

D. Điểm P là điểm biểu diễn số phức ${\mathrm{z}}_3=-1-2\mathrm{i}$

Xem lời giải »

Câu 8:

Gọi A, B lần lượt là điểm biểu diễn cho hai số phức ${\mathrm{z}}_1=1+\mathrm{i}$ và ${\mathrm{z}}_2=1-3\mathrm{i}$. Gọi M là trung điểm của AB. Khi đó M là điểm biểu diễn cho số phức nào dưới đây?

A. $1-\mathrm{i}$

B. $2-2\mathrm{i}$

C. $\mathrm{c}-\mathrm{i}$

D. $1+\mathrm{i}$

Xem lời giải »

Câu 9:

Gọi A là điểm biểu diễn số phức $\mathrm{z}=4-7\mathrm{i}$ và B là điểm biểu diễn của số phức $\mathrm{z}\text{'}=-4+7\mathrm{i}$. Mệnh đề nào sau đây là đúng?

A. Hai điểm A và B đối xứng với nhau qua trục hoành.

B. Hai điểm A và B đối xứng nhau qua trục tung

C. Hai điểm A và B đối xứng nhau qua gốc tọa độ O

D. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.

Xem lời giải »