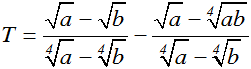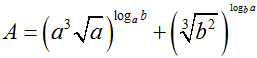Top 100 Bài tập ôn tập chương II (mới nhất)
Haylamdo biên soạn và sưu tầm với 50 Bải tập ôn tập chương II Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Bài tập ôn tập chương II
Câu 1:
Tìm tập xác định D của hàm số y = ( x2 - 3x + 2) 100
A. D = [1; 2]
B. D = [2; +∞) ∪ (-∞; 1]
C. D = R
D. D = ( 1; 2)
Xem lời giải »
Câu 2:
Tìm tập xác định D của hàm số y = ( x3 - 8) -100
A. D = ( 2; + ∞)
B. D = R \ {2}
C. D = ( -∞; 2)
D. D = R \ ( -2; 2)
Xem lời giải »
Câu 3:
Tìm tập xác định D của hàm số y = ( x3 - 8)0
A. D = [2; +∞)
B. D = R\{2}
C. D = ( -∞; 2)
D. R
Xem lời giải »
Câu 4:
Tìm x để biểu thức (2x - 1)– 2 có nghĩa:
A. x ≠
B. x >
C. < x < 2
D. x < 2
Xem lời giải »
Câu 5:
Tìm tập xác định D của hàm số
A. D = R
B. D = [4; +∞) ∪ (-∞; 2]
C. D = (4; +∞) ∪ (-∞; 2)
D. D = [2; 4]
Xem lời giải »
Câu 6:
Tìm x để biểu thức có nghĩa:
A. R
B. Không tồn tại x
C. x > 1
D. x khác 0
Xem lời giải »
Câu 8:
Đơn giản biểu thức 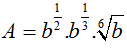 ( b>0) ta được:
( b>0) ta được:
A. A= b2
B.
C. A = b
D.
Xem lời giải »
Câu 9:
Nếu thì:
A. a < 1; 0 < b < 1.
B. a > 1; b < 1.
C. 0 <a < 1; b < 1.
D. a > 1; 0 < b < 1.
Xem lời giải »
Câu 10:
Nếu thì
A. mọi x
B. x < 1
C. x > -1
D. x < -1
Xem lời giải »
Câu 11:
Tìm biểu thức không có nghĩa trong các biểu thức sau:
A. ( -3) -4.
B. ( -3) -1/3.
C. 04.
D.
Xem lời giải »
Câu 12:
Đơn giản biểu thức 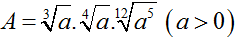 ta được:
ta được:
A . A = a2
B. A = a5/6
C. A = a2/3
D. A= a
Xem lời giải »
Câu 14:
Cho , khi đó f( 1,3) bằng:
A. 0,13
B.1,3
C. 0,013
D. 13
Xem lời giải »
Câu 15:
Cho . Khi đó f( 2,7) bằng
A. 0,027
B. 0,27
C. 2,7
D. 27
Xem lời giải »
Câu 16:
Đơn giản biểu thức ,ta được:
A. -9a2|b|.
B. 9a2|b|.
C. 9a2b.
D. 3a2|b|.
Xem lời giải »
Câu 17:
Đơn giản biểu thức 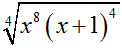 , ta được:
, ta được:
A. x2( x + 1)
B. –x2(x + 1)
C. x2( x - 1)
D. x2|x + 1|
Xem lời giải »
Câu 18:
Đơn giản biểu thức 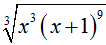 , ta được:
, ta được:
A. –x( x+ 1) 3.
B. x(x + 1) 3.
C. |x(x + 1)3|.
D. x|(x + 1)3|.
Xem lời giải »
Câu 19:
Với giá trị nào của x thì đẳng thức  đúng
đúng
A. x ≠ 0
B. x ≥ 0
C. x = ± 1
D. Không có giá trị nào
Xem lời giải »
Câu 20:
Đơn giản biểu thức 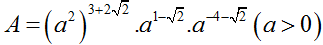 ta được:
ta được:
A.
B.
C.
D.
Xem lời giải »
Câu 21:
Trong các biểu thức sau biểu thức nào không có nghĩa
A. (-2016)0.
B. ( -2016)2016.
C. 0- 2016.
D. ( -2016) -2016 .
Xem lời giải »
Câu 22:
Đơn giản biểu thức 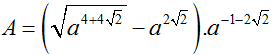 ta được:
ta được:
A. A = a - 1/a
B. a2 - 1/a
C.
D. A = a2 - a
Xem lời giải »
Câu 24:
Đơn giản biểu thức 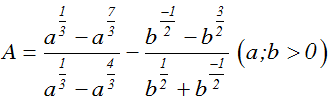 ta được:
ta được:
A. A = a + b
B. A = a - b
C. A = a + b + 2
D. A = a – b + 2
Xem lời giải »
Câu 25:
Đơn giản biểu thức: 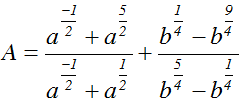 ta được:
ta được:
A. A = a2 + b
B. A = a2 + a - b
C. A = a2 – a – b
D. A = -(a + b)
Xem lời giải »
Câu 26:
Đơn giản biểu thức ( a; b> 0; ab) , ta được
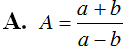
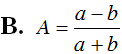
C. A = 1
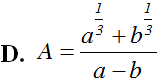
Xem lời giải »
Câu 27:
Cho 2x = 3.Tính giá trị biểu thức A = 4x + 3.2-x - 1
A. 8
B. 9
C. 10
D. 11
Xem lời giải »
Câu 28:
Cho 3x = 2. Tính giá trị của biểu thức
A. 39
B. 25
C. A = 81/2
D. A = 45/2
Xem lời giải »
Câu 29:
Biết rằng 2x = 5. Tính giá trị của biểu thức 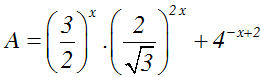
A. A = 28/5
B. A = 31/3
C. A = 6
D. A = 141/25
Xem lời giải »
Câu 30:
Cho 2x = a; 3x = b. Hãy biểu diễn A = 24x + 6x + 9x theo a và b.
A. A =
B. A =
C. A =
D. A =
Xem lời giải »
Câu 1:
Cho . hãy tính giá trị của biểu thức 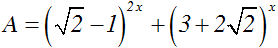
A. A = 18
B. A = 0
C. A = 82/9
D. A = 28/9
Xem lời giải »
Câu 2:
Cho 5x = 4 hãy tính giá trị của biểu thức
A. T = 14
B. T = 47/4
C. T = 118
D. T = 6
Xem lời giải »
Câu 3:
Cho a = 2x; b = 5x. Hãy biểu diễn T = 20x + 50x theo a và b.
A. T = ab(a + b)
B.
C. T = a2 + ab2
D. T = ab + a2b
Xem lời giải »
Câu 4:
Cho và ax > bx. Khẳng định nào sau đây là đúng
A. 1 > a > b > 0
B. 1 > b > a > 0
C. a > b > 1
D. b > a > 1
Xem lời giải »
Câu 5:
So sánh hai số m và n nếu
A. m > n.
B. m = n
C. m < n
D. Không so sánh được
Xem lời giải »
Câu 6:
So sánh hai số m và n nếu 
A. Không so sánh được.
B. m = n.
C. m > n.
D. m < n.
Xem lời giải »
Câu 7:
So sánh hai số m và n nếu 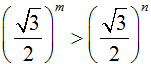
A. m < n
B. m = n
C. m > n
D. Không so sánh được
Xem lời giải »
Câu 8:
Cho và . Khẳng định nào sau đây là đúng
A. a, b >1
B. 0 < a < 2; b > 1
C. 0 < a < 2; b < 1
D. a > 2; b > 1
Xem lời giải »
Câu 9:
Khẳng định nào dưới đây là đúng
A. ( x2 + 1) 2017 > ( x2 + 1) 2017
B.
C.
D. Cả A và C đều đúng
Xem lời giải »
Câu 10:
Kết luận nào đúng về số thực a nếu ( 2a + 1) -3 > ( 2a + 1)-1
A.
B. -1/2 < a < 0.
C.
D. a < -1.
Xem lời giải »
Câu 11:
Kết luận nào đúng về số thực a nếu 
A. 0 < a < 1
B. a > 0
C. a > 1
D. a < 0
Xem lời giải »
Câu 12:
Kết luận nào đúng về số thực a nếu 
A. a < 1
B. a > 0
C. 0 < a < 1
D. a <0
Xem lời giải »
Câu 13:
Kết luận nào đúng về số thực a nếu 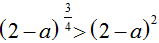
A. a > 1
B.0 < a < 1
C. 1 < a < 2
D. a < 1
Xem lời giải »
Câu 14:
Cho và . Khẳng định nào dưới đây là đúng?
A. 2 < a < b < 3
B. 2 < b < a < 3
C. b > a > 3
D. a > b > 3
Xem lời giải »
Câu 16:
Trong các số a thoã mãn điều kiện dưới đây. Số nào lớn hơn 1.
A. log2a = -2
B. log3a = π
C. log4a2 = -1
D. log3a = - 0, 4
Xem lời giải »
Câu 17:
Trong các số a thoả mãn điều kiện dưới đây. Số nào nhỏ hơn 1.
A. 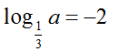
B. loga5 = 2
C. log35 = a
D. 
Xem lời giải »
Câu 18:
Giá trị của biểu thức 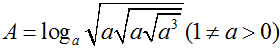 là
là
A. a = 4/3
B. a = 3/4
C. a = 8/9
D. a = 9/8
Xem lời giải »
Câu 19:
Giá trị của biểu thức  là:
là:
A. A = 1/4
B. A = 1/3
C. A = 1/2
D. A = 3/4
Xem lời giải »
Câu 20:
Giá trị của biểu thức  là:
là:
A. A = 17/5
B. A = 37/10
C. A = 21/5
D. A = 39/10
Xem lời giải »
Câu 21:
Cho 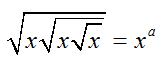 và
và 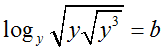 ( với x ; y > 0 và y ≠ 1). Tính A = a + b bằng
( với x ; y > 0 và y ≠ 1). Tính A = a + b bằng
A. A = 9/4
B. A = 3/2
C. A = 15/8
D. A = 17/8
Xem lời giải »
Câu 22:
Cho  và
và 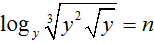 ( với x ; y > 0 ; y ≠ 1). Tính A = m + n
( với x ; y > 0 ; y ≠ 1). Tính A = m + n
A. A = 23/12
B . A = 1
C. A = 3
D. A = 7/3
Xem lời giải »
Câu 24:
Thu gọn biểu thức  ta được:
ta được:
A. A = a5 + b3
B. A = a3 + b5
C. A = a3 + b3
D. A = a5 + b5
Xem lời giải »
Câu 25:
Thu gọn biểu thức (a 1, b>0) Ta được
A. 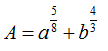
B. 
C. 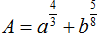
D. 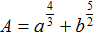
Xem lời giải »
Câu 26:
Cho logab= 2 và logac= 3. Tính P=loga( b2c3)
A. P=108
B. P=13
C. P =31
D.P =30
Xem lời giải »
Câu 27:
Cho log3x= 4log3a+ 2log3b( a ; b> 0) . Khi đó
A.x= 8ab
B. x= a4+ b2
C.
D. x= a4b2
Xem lời giải »
Câu 28:
Cho ( a;b > 0)Khi đó:
A. 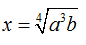
B.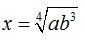
C. 
D. 
Xem lời giải »
Câu 29:
Tìm điều kiện xác định của biểu thức
A.
B.
C.
D.
Xem lời giải »
Câu 30:
Với giá trị nào của x thì biểu thức C= ln( 4- x2) xác định?
A.-2< x< 2
B.-2≤ x≤ 2.
C.x> 2
D. x< -2
Xem lời giải »
Câu 1:
Với giá trị nào của x thì biểu thức xác định?
A.-3≤ x≤ 1.
B. 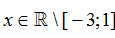
C.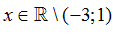
D. .-3< x < 1.
Xem lời giải »
Câu 2:
Với giá trị nào của x thì biểu thức: f( x) = log6( 2x- x2) xác định?
A.0<x< 2.
B. x> 2.
C.-1< x< 1.
D.x< 3.
Xem lời giải »
Câu 3:
Với giá trị nào của x thì biểu thức: f(x) = log5( x3-x2-2x) xác định?
A. 0<x < 1.
B x> 1
C. 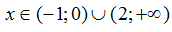
D.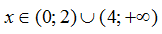
Xem lời giải »
Câu 4:
Điều kiện xác định của biểu thức là
A. 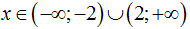
B. x>3
C. 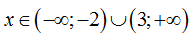
D. 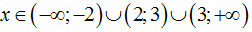
Xem lời giải »
Câu 5:
Cho Khi đó:
A. 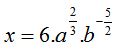
B. 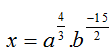
C. 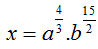
D. x= ab
Xem lời giải »
Câu 6:
Cho logax= m và logabx= n ( a; b> 0) . Khi đó logbx bằng
A.
B. 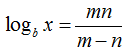
C. 
D. 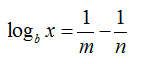
Xem lời giải »
Câu 7:
Cho x= 2000! . Giá trị của biểu thức là:
A. 1
B. -1
C.1000
D.2000
Xem lời giải »
Câu 8:
Rút gọn biểu thức ta được:
A. 
B
C. 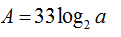
D. 
Xem lời giải »
Câu 9:
Rút gọn biểu thức A= log4a- log8a+ log16a2 ( a> 0) ta được:
A. A= log2x
B. 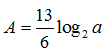
C. 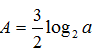
D. 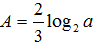
Xem lời giải »
Câu 10:
Cho . Tính giá trị của biểu thức
A. A =
B. A = -2
C.
D. A =
Xem lời giải »
Câu 11:
Rút gọn biểu thức Ta được:
A.
B.
C.
D.
Xem lời giải »
Câu 12:
Rút gọn biểu thức A= log3x.log23+ log5x.log45 ( x> 0) ta được:
A. 
B. 
C.A= 2log2x
D.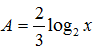
Xem lời giải »
Câu 13:
Cho . Tính giá trị biểu thức:
A.
B.
C. A = -2(1+)
D. A = 3(1 + )
Xem lời giải »
Câu 14:
Tính giá trị của biểu thức
A. -18
B.
C. 18
D.
Xem lời giải »
Câu 15:
Tình giá trị của biểu thức
A. -18
B.
C. 18
D.
Xem lời giải »
Câu 16:
Tính giá trị của biểu thức
A. 3
B. 12
C.
D.
Xem lời giải »
Câu 17:
Cho ln x= 2. Tính giá trị của biểu thức
A. T = 21
B . T =12
C . T = 13
D. T =7
Xem lời giải »
Câu 18:
Cho lnx= 3. Tính giá trị của biểu thức
A. T = 16
B . T = 15
C.T =
D. T = 22
Xem lời giải »
Câu 19:
Cho logab= 3 ; logac = -2. Tính giá trị của logax biết rằng
A. 16
B. 6
C. 13
D. 3
Xem lời giải »
Câu 20:
Cho logab= 2 ; logac= 3. Tính giá trị của biểu thức logax, biết rằng
A. -6
B. -4
C. -2
D. -1
Xem lời giải »
Câu 21:
Cho các số thực dược a,b,c với a,b,ab. Khẳng định nào sau đây là sai.
A.
B.
C.
D.
Xem lời giải »
Câu 22:
Cho các số dương a; b và a≠ 1. Khẳng định nào dưới đây là sai
A. 
B. 
C. 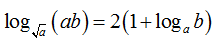
D. 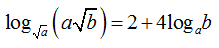
Xem lời giải »
Câu 23:
Cho các số dương a và b. Khẳng định nào dưới đây là sai.
A.
B.
C.
D.
Xem lời giải »
Câu 24:
Cho các số dương a; b; c; và a khác 1. Khẳng định nào sau đây là sai.
A. 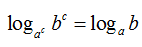
B. 
C. 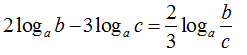
D. 
Xem lời giải »
Câu 25:
Đặt a= log23 . Hãy tính log2 48 theo a
A. 3+ 2a
B. 4+ 2a
C. 4+ a
D. 5- a
Xem lời giải »
Câu 26:
Cho log25= a. Hãy tính log41250 theo a
A. 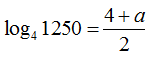
B. 
C. 
D. 
Xem lời giải »
Câu 28:
Cho . Hãy biểu diễn log25 theo a
A. 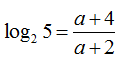
B. 
C. 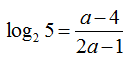
D. 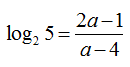
Xem lời giải »
Câu 29:
Cho log1812= a. Hãy biểu diễn log23 theo a
A. 
B. 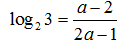
C. 
D. 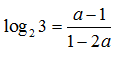
Xem lời giải »
Câu 30:
Đặt log23= a và log35= b. Hãy biểu diễn log245 theo a và b
A. 2a+ 2ab
B.a+ ab
C. 3a+ ab
D.2a+ ab
Xem lời giải »
Câu 1:
Cho x > 0 và y > 0. Viết biểu thức ; về dạng và biểu thức về dạng . Ta có m – n = ?
A. -11/6
B. 11/6
C. 8/5
D. -8/5
Xem lời giải »
Câu 2:
Viết biểu thức về dạng và biểu thức về dạng 2y. Ta có x + y bằng
A.
B.
C.
D.
Xem lời giải »
Câu 3:
Đơn giản biểu thức ta được:
A.
B.
C.
D.
Xem lời giải »
Câu 4:
Cho a + b = 1 thì bằng
A. 4.
B. 2.
C. 3.
D. 1.
Xem lời giải »
Câu 5:
Đơn giản biểu thức ta được:
A. A = a - b
B. A = a
C. A = 1/a
D. A = a + b
Xem lời giải »
Câu 6:
Biết 4x + 4-x = 23 tính giá trị của biểu thức P = 2x + 2-x:
A. 5
B.
C.
D. 25
Xem lời giải »
Câu 7:
Đơn giản biểu thức: ta được:
A.
B.
C.
D.
Xem lời giải »
Câu 8:
Đặt log23 = a và log35 = b. Hãy biểu diễn log1215 theo a và b.
A.
B.
C.
D.
Xem lời giải »
Câu 9:
Đặt a = log23 ; b = log53 . Hãy biểu diễn log645 theo a và b.
A.
B.
C.
D.
Xem lời giải »
Câu 10:
Cho a = log35; b = log75. Khi đó khẳng định nào sau đây đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 11:
Cho a = log23; b = log35 . Khi đó log1290 tính theo a; b bằng:
A.
B.
C.
D.
Xem lời giải »
Câu 12:
Cho a = log53; b = log75 . Tính log15105 theo a và b.
A.
B.
C.
D.
Xem lời giải »
Câu 13:
Cho a = log32 và b = log35. Tính log10 60 theo a và b.
A.
B.
C.
D.
Xem lời giải »
Câu 14:
Nếu log83 = p và log35 = q thì log 5 bằng:
A.
B.
C. p.q
D.
Xem lời giải »
Câu 15:
Biết log275 = a; log87 = b; log23 = c thì log12 35 tính theo a; b; c bằng:
A.
B.
C.
D.
Xem lời giải »
Câu 16:
Cho log23 = a; log35 = b; log72 = c . Hãy tính log14063 theo a; b; c
A.
B.
C.
D.
Xem lời giải »
Câu 17:
Cho logba = x và logbc = y . Hãy biểu diễn theo x và y:
A.
B.
C.
D.
Xem lời giải »
Câu 18:
Cho , với a> 1 ; b> 1 và . Tìm m sao cho P đạt giá trị nhỏ nhất.
A. m = 1.
B. m = 1/2 .
C. m = 4.
D.m = 2.
Xem lời giải »
Câu 19:
Cho log26 = a và log35 = b . Hãy tính theo a,b.
A..
B.
C.
D.
Xem lời giải »
Câu 20:
Cho các số thực a; b > 0. Khẳng định nào sau đây là đúng ?
A.
B.
C.
D.
Xem lời giải »
Câu 21:
Cho các số thực dương x; y > 0 thỏa mãn x2 + y2 = 8xy. Khẳng định nào sau đây là đúng ?
A.
B. log( x + y) = logx + log y + 1
C. log(x + y) = logx + logy - 1
D. log(x + y) = 10( logx + logy)
Xem lời giải »
Câu 22:
Cho các số thực dương x; y thỏa mãn x2 + y2 = 14. Khẳng định nào sau đây là đúng ?
A. =x+y
B. =x+y
C.
D.
Xem lời giải »
Câu 23:
Cho các số thực x; y và x2 + y2 = 3xy. Khẳng định nào sau đây là đúng
A.
B.
C. log5(x + y) 2 = 1 + log5( xy)
D. Tất cả đều đúng
Xem lời giải »
Câu 24:
Cho logax = p; logbx = q; logcx = r ( a; b; c ≠ 1 và x > 0) . Hãy tính logabcx
A.
B.
C.
D.
Xem lời giải »
Câu 25:
Rút gọn biểu thức: là:
A. 0
B. 1
C. 3
D. 2
Xem lời giải »
Câu 1:
Rút gọn
A. logx2012!
B.logx1002!
C.logx2011!
D. logx2011.
Xem lời giải »
Câu 2:
Kết quả rút gọn của biểu thức là:
A. logab
B.
C.
D.
Xem lời giải »
Câu 3:
Cho a; b > 0, Nếu viết thì xy bằng bao nhiêu ?
A. -1/3
B. 1/3
C. 3
D. - 3
Xem lời giải »
Câu 4:
Thu gọn biểu thức ta được:
A.
B.
C.
D.
Xem lời giải »
Câu 5:
Cho các số thực a; b; c thỏa mãn: . Giá trị của biểu thức là:
A. 519
B. 729
C. 469
D. 129
Xem lời giải »
Câu 6:
Tính giá trị của biểu thức
A. P = 1
B. P = 1/2
C. P = 0
D. P = 2
Xem lời giải »
Câu 7:
Cho x; y là các số thực lớn hơn thoả mãn x2 + 9y2 = 6xy . Tính
A. M = 1/4.
B. M = 1.
C. M = 1/2.
D. M = 1/3.
Xem lời giải »
Câu 8:
Cho f(1) = 1; f(m + n) = f(m) + f( n) + m.n với các số nguyên dương m; n .Khi đó giá trị của biểu thức là
A. 3
B. 4
C. 6
D. 9
Xem lời giải »
Câu 9:
Xét các số thực a; b thỏa mãn a > b > 1 . Tìm giá trị nhỏ nhất của P của biểu thức
A. 19.
B. 13.
C. 14.
D. 15.
Xem lời giải »
Câu 10:
Cho log9x = log12y = log16 (x + y). Giá trị của tỉ số x/y là:
A.
B.
C.
D.
Xem lời giải »
Câu 11:
Cho x; y > 0 thỏa mãn log2x + log2y = log4( x + y) Tìm x; y để biểu thức P = x2 + y2 đạt giá trị nhỏ nhất.
A.
B.
C. x = y= 1
D.
Xem lời giải »
Câu 12:
Cho với b> a > 1 và P = log2ab + 54logba. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là?
A. 2
B. 3
C. 4
D. 5
Xem lời giải »
Câu 13:
Cho a; b; c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c - b và c + b khác 1. Khi đó logc+ba + logc-ba bằng:
A.-2logc+ba.logc-ba.
B. 3logc+ba.logc-ba.
C.2logc+ba.logc-ba.
D. Tất cả sai
Xem lời giải »
Câu 14:
Cho hai số thực a; b với 1< a< b. Khẳng định nào sau đây là khẳng định đúng?
A. logab < 1 < logba
B. b < loga1 < log ba
C. logab < logba < 1
D. logba < 1 < logab
Xem lời giải »
Câu 15:
Cho a; b > 0 thỏa mãn a2 + b 2 = 7ab. Chọn mệnh đề đúng trong các mệnh đề sau?
A. 3log(a+b) = (loga+logb)
B.
C. 2( loga + logb) = log( 7ab) .
D. log(a+b) =(loga+logb)
Xem lời giải »
Câu 16:
Cho x; y; z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = logxy; b = logzy. Mệnh đề nào sau đây đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 17:
Cho các số dương a; b thõa mãn 4a2 + 9b2 = 13ab . Chọn câu trả lời đúng.
A. log=log+2log
B. log(2a+3b)=3log a+2logb
C. log=(loga+logb)
D. log=(loga+logb)
Xem lời giải »
Câu 18:
Cho x; y > 0 và x2 + 4y2 = 12xy . Khẳng định nào sau đây là khẳng định đúng?
A. log2=log2x-log2y
B. log2(x+2y)=2+(log2x+log2y)
C. log2(x + 2y) = log2x+log2y+1
D. 4log2( x + 2y) = log2x + log2y.
Xem lời giải »
Câu 19:
Cho a; b; c> 0 đôi một khác nhau và khác 1, khẳng định nào sau đây là khẳng định đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 20:
Cho a; b là các số thực dương thoả mãn a2 + b2 = 14ab . Khẳng định nào sau đây là sai ?
A.
B. 2log2(a + b) = 4 + log2a + log2b.
C. 2log4(a + b) = 4 + log4a + log4b.
D.
Xem lời giải »
Câu 21:
Với giá trị nào của m thì biểu thức xác định với mọi ?
A. m > -3
B. m < 3
C.
D.
Xem lời giải »
Câu 22:
Biểu thức ln( x2 - 2mx + 4) có nghĩa với mọi x khi
A. m = 2
B. -2 < m < 2
C. 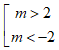
D. m < 2
Xem lời giải »
Câu 23:
Tìm x để ba số ln2; ln( 2x - 1); ln( 2x + 3) theo thứ tự lập thành cấp số cộng.
A. 1
B. 2
C. log25
D. log23
Xem lời giải »
Câu 24:
Biểu thức T = log2( ax2 - 4x + 1) có nghĩa với mọi x khi
A. 0 < a < 4
B. a > 0
C. a > 4
D.
Xem lời giải »
Câu 25:
Với giá trị nào của m thì biểu thức T = 34 + ln( 4m - x) xác định với mọi ?
A. m > -4
B. m -1/4
C. m < -4
D. m > -1/4
Xem lời giải »
Câu 1:
Cho hàm số y = log2( 4x - 2x + m) có tập xác định D = R khi:
A.
B. m > 1/4
C. m < -1/4
D. m > 0
Xem lời giải »
Câu 2:
có tập xác định D = R khi đó có bao nhiêu giá trị nguyên dương của tham số m ?
A. 1
B. 5
C. 10
D. 13
Xem lời giải »
Câu 3:
Cho hàm số . Mệnh đề nào dưới đây là đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 4:
Cho x; y là các số thực dương thỏa . Tính tỉ số x/y
A. x/y = 4
B. x/y = 3
C. x/y = 5
D. x/y = 2
Xem lời giải »
Câu 5:
Đồ thị hàm số trong hình bên là đồ thị hàm số nào trong các hàm số dưới đây.
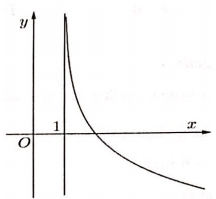
A. y = ln( x - 1)
B.
C. y = 2x-1
D.
Xem lời giải »
Câu 6:
Cho hàm số sau: y = f(x) = ( x2 - 2( m + 4) x + 2m + 12).ex. Tìm tổng các giá trị nguyên của m để hàm số nghịch biến trên TXĐ là S thì giá trị của S sẽ là:
A. 15
B. -12
C. -15
D. -10
Xem lời giải »
Câu 7:
Cho là các số thực. Đồ thị các hàm số trên khoảng được cho hình vẽ bên. Khẳng định nào sau đây đúng?

A.
B.
C.
D.
Xem lời giải »
Câu 8:
Trong hình vẽ bên đồ thị (1) là của hàm số y = logax và đồ thị (2) là của hàm số y = logbx. Khẳng định nào sau đây là đúng.
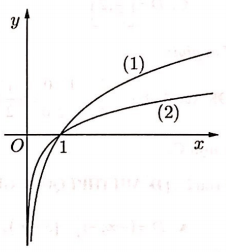
A. a > b > 1
B. b > a > 1
C. 1 > a > b > 0
D. 1 > b > a > 0
Xem lời giải »
Câu 9:
Hỏi có bao nhiêu giá trị nguyên của m để phương trình 3x+m2=10m-9 có nghiệm thực?
A. 7
B. 9
C. 6
D. 10
Xem lời giải »
Câu 10:
Cho hàm số có giá trị nhỏ nhất trên [1; e] bằng -3. Chọn khẳng định đúng về tham số m?
A. m > 2
B. m > 5
C. m < 3
D. m < 0
Xem lời giải »
Câu 11:
Tìm tất cả các giá trị của tham số m sao cho hàm số đồng biến trên khoảng
A. 1 < m < 2
B.
C.
D. 1 ≤ m ≤ 2
Xem lời giải »
Câu 12:
Cho hai số thực dương a ; b khác 1 Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt các đường y = ax; y =bx và trục tung lần lượt tại M ; N ; A thì AN = 3AM ( hình vẽ bên ).
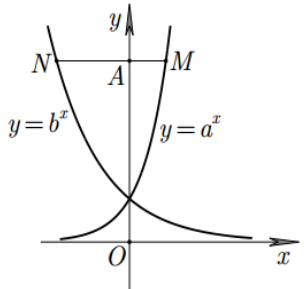
Hỏi khẳng định nào sau đây đúng ?
A. ab2 = 1
B. b = 3a
C. a3b = 1
D. ab3 = 1
Xem lời giải »
Câu 13:
Tập xác định của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 14:
Tập xác định của hàm số y = log2( log3x - 1) là:
A.
B.
C.
D.
Xem lời giải »
Câu 15:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 16:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 17:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 18:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 19:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 20:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 21:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 22:
Đạo hàm của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 23:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là:
A.
B.
C.
D.
Xem lời giải »
Câu 24:
Giá trị lớn nhất và nhỏ nhất của hàm số y = 4x - 2x+1 trên đoạn [- 1;1]
A.
B.
C.
D.
Xem lời giải »
Câu 25:
Giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [0;1] là:
A.
B.
C.
D.
Xem lời giải »
Câu 1:
Xét các số thực dương thỏa mãn . Tìm giá trị nhỏ nhất Smin của S = x + y
A.
B.
C.
D. Đáp án khác
Xem lời giải »
Câu 2:
Cho hai số thực dương a; b thỏa mãn log2(a + 1) + log2(b + 1) ≥ 6 Giá trị nhỏ nhất của biểu thức S = a + b là
A.12
B.14
C. 8
D.16
Xem lời giải »
Câu 3:
Xét các số thực a; b thỏa mãn a > b > 1 Tìm giá trị nhỏ nhất Pmin của biểu thức
A.19
B.13
C.14
D.15
Xem lời giải »
Câu 4:
Số nghiệm của phương trình: là
A. 0
B. 1
C. 2
D. 3
Xem lời giải »
Câu 5:
Phương trình có bao nhiêu nghiệm?
A. 2.
B. 1.
C. 4.
D. 3.
Xem lời giải »
Câu 6:
Phương trình có bao nhiêu nghiệm âm?
A. 1
B. 3
C. 2
D. 0
Xem lời giải »
Câu 7:
Biết rằng phương trình có hai nghiệm phân biệt là x1 ; x2 .Tổng có dạng a + b log2 3 , với a ; b nguyên . Tính S = a2 + 5ab.
A. 45
B. 96
C. 39
D. 126
Xem lời giải »
Câu 8:
Gọi x1; x2 là hai nghiệm của phương trình . Khi đó, tổng hai nghiệm bằng?
A. 0.
B. 2.
C. -2.
D. 1.
Xem lời giải »
Câu 9:
Tính tổng T tất cả các nghiệm của phương trình trên đoạn
A.
B.
C.
D. T = 0
Xem lời giải »
Câu 10:
Tính tổng các nghiệm của phương trình ?
A. 1.
B. 2.
C. 3.
D. 0.
Xem lời giải »
Câu 11:
Tính S là tổng tất cả các nghiệm của phương trình 4( 22x + 2-2x)– 4( 2x + 2-x) - 7 = 0.
A. S = 1
B. S = -1
C. S = 3
D. S = 0
Xem lời giải »
Câu 12:
Biết rằng phương trình có nghiệm duy nhất x = x0. Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 13:
Phương trình 3.25x-2 + (3x - 10) .5x-2 + 3 – x = 0 có tất cả bao nhiêu nghiệm?
A. 1
B. 2
C. 3
D. 4
Xem lời giải »
Câu 14:
Biết phương trình 2x+1. 5x = 15 có nghiệm duy nhất dạng alog5 + blog3 + clog2 với a; b; c nguyên . Tính S = a + 2b + 3c.
A. 2
B. 6
C. 4
D. 0
Xem lời giải »
Câu 15:
Phương trình có hai nghiệm trong đó x1 < x2, hãy chọn phát biểu đúng
A. 3x1 - 2x2 = log38.
B. 2x1 - 3x2 = log38.
C. x1 + x2 = log3486.
D. 3x1 + 2x2 = log354.
Xem lời giải »
Câu 16:
Biết rằng phương trình có nghiệm duy nhất dạng , với a là số thực dương. Mệnh đề nào dưới đây là đúng?
A. 0 < a < 4/5
B. 5 < a < 9
C. 4/5 < a < 12/5
D. 3 < a < 7/2
Xem lời giải »
Câu 17:
Giải phương trình
A.
B.
C.
D.
Xem lời giải »
Câu 18:
Biết rằng phương trình có nghiệm duy nhất dạng với a ; b nguyên . Tính S = a +2b
A. 4
B. 3
C. 7
D. 6
Xem lời giải »
Câu 19:
Phương trình có tất cả bao nhiêu nghiệm?
A. 1.
B. 2.
C. 3.
D. 0.
Xem lời giải »
Câu 20:
Gọi T là tổng tất cả các nghiệm của phương trình . Mệnh đề nào sau đây là đúng?
A. T > 1
B. T = 1
C. -0, 5 < T
D. T < -0,5
Xem lời giải »
Câu 21:
Cho hàm số . Mệnh đề nào sau đây là sai?
A. f(x) = 1 khi
B. f(x) = 1 khi
C. f(x) = 1 khi x2 log35 = 0.
D. f(x) = 1 khi (x + 1)ln3 + x2ln5 = 0.
Xem lời giải »
Câu 22:
Gọi x0 là nghiệm nguyên của phương trình . Tính giá trị của biểu thức P = x0(5 - x0)( x0 + 8).
A.40
B.50
C.60
D.70
Xem lời giải »
Câu 23:
Phương trình có tất cả bao nhiêu nghiệm?
A. 0.
B. 1.
C. 2.
D. 4.
Xem lời giải »
Câu 24:
Tập nghiệm S của phương trình có bao nhiêu nghiệm nguyên trong đó m là tham số khác 2 và m nguyên?
A. 0
B. 1
C. 2
D. 3
Xem lời giải »
Câu 25:
Biết rằng phương trình có đúng hai nghiệm x1; x2. Tính giá trị của
A.
B.
C. P = 26
D.
Xem lời giải »
Câu 1:
Khẳng định nào sau đây là đúng?
A. ln(-e) = -1
B. ln10 = (ln2)(ln5)
C.
D.
Xem lời giải »
Câu 2:
Lôgarit cơ số 3 của là:
A. 3
B. 5
C.
D.
Xem lời giải »
Câu 3:
Tính giá trị biểu thức ?
A. 0
B. -6
C. 7
D.
Xem lời giải »
Câu 4:
Giải phương trình
A. x = 2log4
B. x = 4log2
C. x = 2log2 + 2
D. x = 4
Xem lời giải »
Câu 5:
Nếu thì x bằng
A. 0,8
B. 0,81
C. 1,25
D. 2,43
Xem lời giải »
Câu 6:
Giải bất phương trình
A. x ≤ 2
B. x ≤ -2
C. x ≥ 2
D. x ≥ -2
Xem lời giải »
Câu 7:
Giải bất phương trình
A.
B.
C.
D.
Xem lời giải »
Câu 9:
Tìm các điểm cực trị của hàm số
A. x = -1
B. x = 1
C. x = 1/2
D. x = 2
Xem lời giải »
Câu 10:
Đặt log2 = a, log3 = b . Khi đó bằng
A.
B.
C.
D.
Xem lời giải »
Câu 11:
Tìm các đường tiệm cận ngang của đồ thị hàm số
A. y = 0
B. y = -1
C. y = 0 và y = 1
D. y = 0 và y = -1
Xem lời giải »
Câu 12:
Ngày 27 tháng 3 năm 2016 bà Mai gửi tiết kiệm vào ngân hàng số tiền 100 triệu đồng với hình thức lãi kép và lãi suất 6,8% một năm. Bà Mai dự tính đến ngày 27 tháng 3 năm 2020 thì rút hết tiền ra để lo công chuyện. Hỏi bà sẽ rút được bao nhiêu tiền (làm tròn kết quả đến hàng nghìn)
A. 38949000 đồng
B. 21818000 đồng
C. 31259000 đồng
D. 30102000 đồng
Xem lời giải »
Câu 13:
Tính đạo hàm của hàm số
A.
B.
C.
D.
Xem lời giải »
Câu 14:
Cho hàm số
Khẳng định nào sau đây đúng ?
A. là điểm cực đại của hàm số
B. là điểm cực tiểu của hàm số
C. là điểm cực đại của hàm số
D. là điểm cực tiểu của hàm số
Xem lời giải »
Câu 15:
Giải phương trình
A.
B.
C.
D.
Xem lời giải »
Câu 16:
Tính tổng bình phương các nghiệm của phương trình
A. 4
B. 8
C. 12
D. 16
Xem lời giải »
Câu 17:
Tính tổng bình phương các nghiệm của phương trình
A. 4
B. 8
C. 12
D. 16
Xem lời giải »
Câu 18:
Nếu thì x bằng
A.
B.
C. 125
D. 243
Xem lời giải »
Câu 19:
x là nghiệm của phương trình . Hãy tính
A. x = 3
B.
C.
D.
Xem lời giải »
Câu 20:
Giả sử x là nghiệm của phương trình Tính
A. 1
B. 8
C.
D.
Xem lời giải »
Câu 21:
Giải bất phương trình
A. 1 ≤ x ≤ 4
B. 0 ≤ x ≤ 4
C. 1 ≤ x ≤ 5
D. 0 ≤ x ≤ 5
Xem lời giải »
Câu 22:
Giải bất phương trình
A. x ≤ 0
B. x ≥ 0
C.
D.
Xem lời giải »
Câu 23:
Giải bất phương trình
A. [-1; 3]
B.
C.
D. (-∞; -1) ∪ (3; +∞)
Xem lời giải »
Câu 24:
Tìm miền xác định của hàm số y = ln(ln(lnx))
A. D = (0; +∞)
B. D = (1; +∞)
C. D = (e; +∞)
D.
Xem lời giải »
Câu 25:
Tìm số x khác 0 thỏa mãn
A. 7
B. 14
C.
D.
Xem lời giải »
Câu 26:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên [-1;4]
A.
B.
C.
D.
Xem lời giải »
Câu 27:
Số lượng của một đàn chim sau thời gian t tháng kể từ khi được quan sát được ước lượng bằng công thức (con). Sau bao lâu kể từ khi được quan sát thì đàn chim có số lượng đông nhất?
A. 1 tháng
B. 4 tháng
C. 5 tháng
D. 8 tháng
Xem lời giải »
Câu 28:
Tìm các giá trị x thỏa mãn ?
A. 2
B. 3
C. 5
D. 6
Xem lời giải »
Câu 29:
Giải phương trình
A. x = 1,
B. x = -1,
C. x = 1,
D. x = -1,
Xem lời giải »
Câu 30:
Cho phương trình . Phương trình nào sau đây không tương đương với phương trình đã cho?
A.
B.
C.
D.
Xem lời giải »
Câu 31:
Cho N > 1 . Tìm số thực x thỏa mãn
A.
B. x = 3840
C. x = log3840
D.
Xem lời giải »
Câu 32:
Cho a và b là hai số thực thỏa mãn Tính giá trị của ab
A. -60
B. -17
C. 12
D. 60
Xem lời giải »
Câu 33:
Ông A gửi tiết kiệm vào ngân hàng 200 triệu đồng với hình thức lãi kép. Sau 5 năm ông rút hết tiền ra được một khoản 283142000 đồng. Hỏi ông A gửi với lãi suất bao nhiêu, biết rằng trong thời gian đó lãi suất không thay đổi?
A. 6,8% một năm
B. 7% một năm
C. 7,2% một năm
D. 8% một năm
Xem lời giải »
Câu 34:
Số lượng cá thể của một mẻ cấy vi khuẩn sau t ngày kể từ lúc ban đầu được ước lượng bởi công thức Sau bao lâu thì số lượng vi khuẩn đạt đến 5000 cá thể? Làm tròn kết quả đến hàng phần mười
A. 10,3 ngày
B. 12,3 ngày
C. 13,0 ngày
D. 61,7 ngày
Xem lời giải »
Câu 35:
Tìm tập nghiệm của bất phương trình
A. (0; 4)
B.
C. (-∞; 1) ∪
D. (0; 1) ∪
Xem lời giải »
Câu 36:
Trong các số được liệt kê trong bốn đáp án A, B, C, D dưới đây, số nào bé nhất?
A.
B.
C.
D.
Xem lời giải »
Câu 37:
Tính giá trị biểu thức:
A. 1
B. 0
C.
D.
Xem lời giải »
Câu 38:
Cho p và q là các số dương thỏa mãn Tính giá trị của
A.
B.
C.
D.
Xem lời giải »
Câu 39:
Gọi P và Q là hai điểm trên đồ thị hàm số lần lượt có hoành độ ln4 và ln16 . Kí hiệu l là độ dài đoạn thẳng PQ. Hệ thức nào sau đây đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 40:
Biết rằng Tính tổng x + y + z
A. 50
B. 58
C. 89
D. 111
Xem lời giải »
Câu 1:
Hàm số nào trong hàm số sau đây có đồ thị phù hợp với hình vẽ bên?
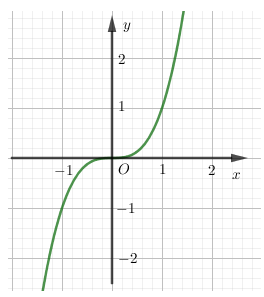
A.
B.
C.
D.
Xem lời giải »
Câu 2:
Cho . Tính theo a và b
A. 5 + 2a + b
B. 5 + 3a + 2b
C. 2 + 2a + 3b
D. 2 + 3a + 2b
Xem lời giải »
Câu 3:
Cho a, b > 0. Khẳng định nào sau đây đúng?
A.
B.
C.
D.
Xem lời giải »
Câu 4:
Trong các hàm số sau, hàm số nào đồng biến trên R?
A.
B.
C.
D.
Xem lời giải »
Câu 5:
Cho hàm số . Tính y''(1)
A.
B.
C.
D.
Xem lời giải »
Câu 6:
Hàm số có tập xác định là:
A.
B.
C.
D.
Xem lời giải »
Câu 7:
Đạo hàm của hàm số là
A.
B.
C.
D.
Xem lời giải »
Câu 8:
Đặt . Hãy biểu diễn theo m
A.
B.
C.
D.
Xem lời giải »
Câu 9:
Giả sử x, y là các số thực dương. Mệnh đề nào sau đây sai?
A.
B.
C.
D.
Xem lời giải »
Câu 10:
Tập nghiệm của bất phương trình là
A. (0;1)
B.
C. (1;8)
D.
Xem lời giải »
Câu 11:
Điều kiện xác định của hệ phương trình là
A.
B.
C.
D.
Xem lời giải »
Câu 12:
Cho hệ phương trình . Chọn khẳng định đúng?
A. Điều kiện xác định của hệ phương trình là x > y > 0
B. Điều kiện xác định của hệ phương trình là x > y
C. Điều kiện xác định của hệ phương trình là
D. Phương trình luôn xác định với mọi x, y
Xem lời giải »
Câu 13:
Tập xác định của hàm số là
A.
B. R
C.
D.
Xem lời giải »
Câu 14:
Số nghiệm của hệ phương trình: là
A. 0
B. 1
C. 2
D. 4
Xem lời giải »
Câu 15:
Tìm tất cả các cặp số (x;y) thỏa mãn và
A. (x;y) = (1;4)
B. (x;y) = (2;3)
C. (x;y) = (2;4)
D. (x;y) = (5;9)
Xem lời giải »
Câu 1:
Biết là hai nghiệm phương trình và với a, b là hai số nguyên dương. Tính a + b
A. 16
B. 11
C. 14
D. 13
Xem lời giải »
Câu 2:
Tính tích tất cả các nghiệm thực của phương trình
A. 0
B. 2
C. 1
D.
Xem lời giải »
Câu 3:
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn . Khi biểu thức đạt giá trị lớn nhất thì giá trị của tổng a+b+c là:
A. 3
B.
C. 4
D. 6
Xem lời giải »
Câu 4:
Cho với và . Khi đó giá trị của m để P đạt giá trị nhỏ nhất là
A. 2
B. 3
C. 4
D. 5
Xem lời giải »
Câu 5:
Tìm số giá trị nguyên của m để phương trình có nghiệm trên [0;1]
A. 2
B. 5
C. 4
D. 3
Xem lời giải »
Câu 6:
Xét bất phương trình . Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng
A.
B.
C.
D.
Xem lời giải »
Câu 7:
Một người tham gia chương trình bảo hiểm An sinh xã hội của công ty bảo Việt với thể lệ như sau: Cứ đến tháng 9 hàng năm người đó đóng vào công ty là 12 triệu đồng với lãi suất hàng năm không đổi là 6%/năm. Hỏi sau đúng 18 năm kể từ ngày đóng, người đó thu về được tất cả bao nhiêu tiền? Kết quả làm tròn đến hai chữ số phần thập phân?
A. 403,32 (triệu đồng)
B. 293,23 (triệu đồng)
C. 412,23 (triệu đồng)
D. 393,12 (triệu đồng)
Xem lời giải »
Câu 8:
Cho hai số thực a, b thỏa mãn và biểu thức có giá trị nhỏ nhất. Tính a + b
A.
B. 4
C. 11
D. 6
Xem lời giải »
Câu 9:
Giá trị nào của m để phương trình có ít nhất 1 nghiệm thuộc đoạn
A.
B.
C.
D.
Xem lời giải »
Câu 10:
Tìm m để tồn tại duy nhất cặp (x;y) thỏa mãn và
A.
B. và
C. và
D.
Xem lời giải »
Câu 11:
Tìm tất cả các giá trị của m để hệ sau có nghiệm
A.
B.
C.
D.
Xem lời giải »
Câu 12:
Biết là hai nghiệm của phương trình và với a, b là hai số nguyên dương. Tính a – b.
A. 3
B. 1
C. 4
D. 6
Xem lời giải »
Câu 13:
Biết rằng trong đó x > 0. Tính giá trị của biểu thức
A. 3
B. 1
C. 2
D. 4
Xem lời giải »
Câu 14:
Cho x, y là các số thực thỏa mãn . Khi 3x + y đạt giá trị lớn nhất, thì giá trị là:
A. k = 1
B. k = 2
C. k = 3
D. k = 4
Xem lời giải »
Câu 15:
Gọi S là tập nghiệm của phương trình . Khi đó số phần tử của tập S là bao nhiêu?
A. 2
B. 3
C. 4
D. 5
Xem lời giải »
Câu 16:
Cho x, y là các số thực dương thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức T = x+y
A.
B.
C.
D.
Xem lời giải »
Câu 17:
Có bao nhiêu số nguyên dương a (a là tham số) để phương trình có nghiệm duy nhất?
A. 2
B. 0
C. Vô số
D. 1
Xem lời giải »
Câu 18:
Xét các số thực dương x, y thỏa mãn . Tìm giá trị lớn nhất của biểu thức
A. 3
B. 2
C. 1
D. 4
Xem lời giải »
Câu 19:
Gọi s là tập hợp tất cả các giá trị của m sao cho và phương trình có nghiệm duy nhất. Tìm số phần tử của S
A. 15
B. 14
C. 13
D. 16
Xem lời giải »
Câu 20:
Xét các số thực a, b thỏa mãn điều kiện . Tìm giá trị nhỏ nhất của biểu thức
A.
B.
C.
D.
Xem lời giải »
Câu 1:
Một người mỗi đầu tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với lãi suất 0,6% mỗi tháng. Biết đến cuối tháng thứ 15 thì người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần với số tiền nào nhất trong các số sau?
A. 635.000
B. 535.000
C. 613.000
D. 643.000
Xem lời giải »
Câu 2:
Xét các số thực dương x, y thỏa mãn . Tìm giá trị của biểu thức
A. 0
B. 1
C. 2
D. 3
Xem lời giải »
Câu 3:
Có bao nhiêu giá trị nguyên m để phương trình có nghiệm trên [0;1]
A. 3
B. 1
C. 4
D. 2
Xem lời giải »
Câu 4:
Xét các số thực dương x, y thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức
A.
B.
C.
D.
Xem lời giải »
Câu 5:
Tìm tất cả các giá trị của tham số m để phương trình có đúng hai nghiệm phân biệt?
A.
B.
C. hoặc
D. hoặc
Xem lời giải »
Câu 6:
Cho với . Biết rằng . Tính giá trị của
A . 2017
B. 2020
C . 2018
D . 2019
Xem lời giải »
Câu 7:
Tập hợp S tất cả các giá trị của tham số m để phương trình có đúng ba nghiệm phân biệt là:
A.
B.
C.
D.
Xem lời giải »
Câu 8:
Cho phương trình với m là tham số. Có bao nhiêu giá trị nguyên của để phương trình đã cho có nghiệm?
A. 9
B. 19
C. 17
D. 18
Xem lời giải »
Câu 9:
Cho a > 0, b > 0 thỏa mãn . Giá trị của a+2b bằng:
A.
B. 5
C. 4
D. 3
Xem lời giải »
Câu 10:
Cho phương trình . Gọi S là tổng tất cả các nghiệm của nó. Khi đó, giá trị của S là:
A.
B. S = 2
C. S = -2
D.
Xem lời giải »
Câu 11:
Cho hàm số . Tính tổng
A.
B.
C.
D.
Xem lời giải »
Câu 12:
Cho hệ có nghiệm (x;y) thỏa mãn . Khi đó giá trị lớn nhất của m là:
A.
B.
C. 5
D. -5
Xem lời giải »
Câu 13:
Hệ phương trình có tất cả bao nhiêu nghiệm (x;y)?
A. 0
B. 1
C. 2
D. 3
Xem lời giải »
Câu 14:
Hệ phương trình có bao nhiêu nghiệm?
A. 0
B. 1
C. Vô số
D. 2
Xem lời giải »
Câu 15:
Cho hệ phương trình . Chọn khẳng định đúng:
A. Điều kiện xác định của hệ phương trình là x > y > 0
B. Hệ phương trình đã cho có 2 nghiệm
C. Hệ phương trình đã cho có 1 nghiệm duy nhất (x;y) = (-1;-2)
D. Hệ phương trình đã cho vô nghiệm
Xem lời giải »
Câu 16:
Tìm tập nghiệm S của hệ phương trình
A.
B.
C.
D.
Xem lời giải »
Câu 17:
Số nghiệm của hệ phương trình là
A. 0
B. 1
C. 2
D. 3
Xem lời giải »
Câu 18:
Xét hệ phương trình có nghiệm (x;y). Khi đó phát biểu nào sau đây đúng:
A. x+y = 1
B. x-y = 0
C.
D. xy = 4
Xem lời giải »
![]() , ta được:
, ta được:![]() , ta được:
, ta được: đúng
đúng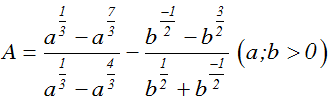 ta được:
ta được: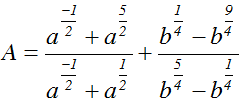 ta được:
ta được: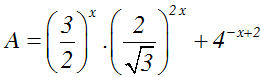
và
![]() ( với x ; y > 0 và y ≠ 1). Tính A = a + b bằng
( với x ; y > 0 và y ≠ 1). Tính A = a + b bằng và
![]() ( với x ; y > 0 ; y ≠ 1). Tính A = m + n
( với x ; y > 0 ; y ≠ 1). Tính A = m + n ta được:
ta được: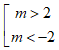





 ta được:
ta được: