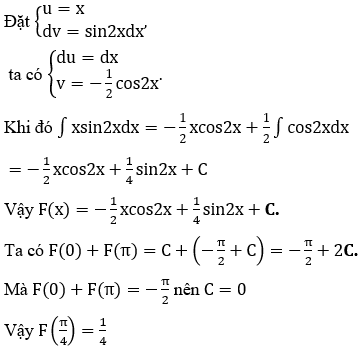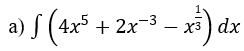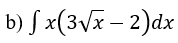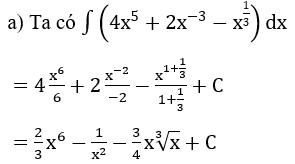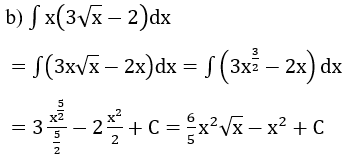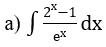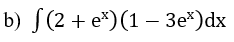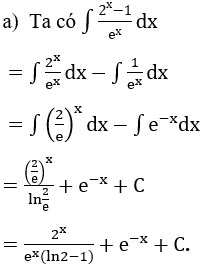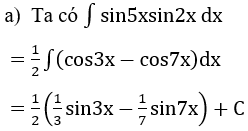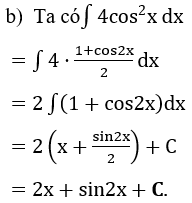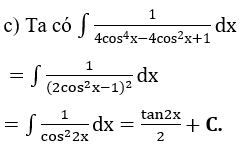Các dạng bài tập Nguyên hàm, Tích phân và ứng dụng chọn lọc, có đáp án - Toán lớp 12
Các dạng bài tập Nguyên hàm, Tích phân và ứng dụng chọn lọc, có đáp án
Với Các dạng bài tập Nguyên hàm, Tích phân và ứng dụng chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 500 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Nguyên hàm, Tích phân và ứng dụng từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Tổng hợp lý thuyết Chương Nguyên hàm, Tích phân và ứng dụng
- Lý thuyết Nguyên hàm Xem chi tiết
- Lý thuyết Tích phân Xem chi tiết
- Lý thuyết Ứng dụng của tích phân trong hình học Xem chi tiết
- Lý thuyết tổng hợp chương Nguyên hàm, Tích phân và ứng dụng Xem chi tiết
Chủ đề: Nguyên hàm
- Bảng công thức nguyên hàm đầy đủ Xem chi tiết
- Phương pháp tính nguyên hàm của các hàm số cơ bản cực hay Xem chi tiết
- Phương pháp tính nguyên hàm đổi biến số cực hay Xem chi tiết
- Phương pháp tính nguyên hàm từng phần cực hay Xem chi tiết
- Dạng 1: Tìm nguyên hàm của hàm số Xem chi tiết
- Trắc nghiệm tìm nguyên hàm của hàm số Xem chi tiết
- Dạng 2: Tìm nguyên hàm bằng phương pháp đổi biến số Xem chi tiết
- Trắc nghiệm tìm nguyên hàm bằng phương pháp đổi biến số Xem chi tiết
- Dạng 3: Tìm nguyên hàm bằng phương pháp từng phần Xem chi tiết
- Trắc nghiệm tìm nguyên hàm bằng phương pháp từng phần Xem chi tiết
- Dạng 4: Tìm nguyên hàm của hàm số hữu tỉ Xem chi tiết
- Trắc nghiệm tìm nguyên hàm của hàm số hữu tỉ Xem chi tiết
- Dạng 5: Tìm nguyên hàm thỏa mãn điều kiện cho trước Xem chi tiết
- Trắc nghiệm tìm nguyên hàm thỏa mãn điều kiện cho trước Xem chi tiết
- Nguyên hàm của hàm đa thức, hàm phân thức Xem chi tiết
- Nguyên hàm của hàm số mũ, hàm số logarit Xem chi tiết
- Nguyên hàm của hàm số lượng giác Xem chi tiết
- Tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số Xem chi tiết
- Tìm nguyên hàm của hàm phân thức bằng phương pháp đổi biến số Xem chi tiết
- Tìm nguyên hàm của hàm số mũ, logarit bằng phương pháp đổi biến số Xem chi tiết
- Tìm nguyên hàm của hàm số lượng giác bằng phương pháp đổi biến số Xem chi tiết
- Tìm nguyên hàm của hàm chứa căn thức bằng phương pháp đổi biến số Xem chi tiết
- Tìm nguyên hàm của hàm lượng giác bằng phương pháp nguyên hàm từng phần Xem chi tiết
- Tìm nguyên hàm của hàm số mũ, logarit bằng phương pháp nguyên hàm từng phần Xem chi tiết
Chủ đề: Tích phân
- Công thức tích phân Xem chi tiết
- Phương pháp tính tích phân cơ bản cực hay Xem chi tiết
- Cách tính tích phân bằng phương pháp đổi biến số cực hay Xem chi tiết
- Phương pháp tính tích phân từng phần cực hay Xem chi tiết
- Phương pháp tính tích phân hàm chứa dấu giá trị tuyệt đối cực hay Xem chi tiết
- Phương pháp tính tích phân hàm số chẵn, hàm số lẻ cực hay Xem chi tiết
- 3 ứng dụng của tích phân: tính diện tích, thể tích, quãng đường, vận tốc cực hay Xem chi tiết
- Dạng 6: Tính tích phân bằng định nghĩa và tính chất Xem chi tiết
- Trắc nghiệm tính tích phân bằng định nghĩa và tính chất Xem chi tiết
- Dạng 7: Tính tích phân từng phần Xem chi tiết
- Trắc nghiệm tính tích phân từng phần Xem chi tiết
- Dạng 8: Tính tích phân bằng phương pháp đổi biến số loại 1 Xem chi tiết
- Trắc nghiệm tính tích phân bằng phương pháp đổi biến số loại 1 Xem chi tiết
- Dạng 9: Tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
- Trắc nghiệm tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
- Dạng 10: Tính tích phân hàm chứa dấu giá trị tuyệt đối Xem chi tiết
- Trắc nghiệm tính tích phân hàm chứa dấu giá trị tuyệt đối Xem chi tiết
- Dạng 11: Tính tích phân hàm số hữu tỉ Xem chi tiết
- Trắc nghiệm tính tích phân hàm số hữu tỉ Xem chi tiết
- Dạng 12: Ứng dụng của tích phân: Tính diện tích hình phẳng Xem chi tiết
- Trắc nghiệm ứng dụng của tích phân: Tính diện tích hình phẳng Xem chi tiết
- Dạng 13: Ứng dụng của tích phân: Tính thể tích khối tròn xoay Xem chi tiết
- Trắc nghiệm ứng dụng của tích phân: Tính thể tích khối tròn xoay Xem chi tiết
- Bài tập về tính chất của tích phân Xem chi tiết
- Bài tập tính tích phân cơ bản Xem chi tiết
- Tính tích phân hàm đa thức, phân thức bằng phương pháp đổi biến số Xem chi tiết
- Tính tích phân hàm lượng giác bằng phương pháp đổi biến số Xem chi tiết
- Tính tích phân hàm số mũ, logarit bằng phương pháp đổi biến số Xem chi tiết
- Tính tích phân hàm chứa căn thức bằng phương pháp đổi biến số Xem chi tiết
- Cách tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
- Bài tập tính tích phân nâng cao Xem chi tiết
- Tính tích phân hàm lượng giác bằng phương pháp tích phân từng phần Xem chi tiết
- Tính tích phân hàm số mũ, logarit bằng phương pháp tích phân từng phần Xem chi tiết
- Tính tích phân của hàm số chẵn, hàm số lẻ Xem chi tiết
- Hàm số dưới dấu tích phân là thương của hàm chẵn và hàm mũ Xem chi tiết
- Tích phân của hàm trị tuyệt đối Xem chi tiết
- Bài tập tích phân nâng cao Xem chi tiết
- Ứng dụng tích phân: Tính diện tích hình phẳng Xem chi tiết
- Ứng dụng tích phân: Tính thể tích vật thể và khối tròn xoay Xem chi tiết
Bài tập trắc nghiệm
- 150 bài tập trắc nghiệm Nguyên hàm, Tích phân và ứng dụng có lời giải (cơ bản) Xem chi tiết
- 150 bài tập trắc nghiệm Nguyên hàm, Tích phân và ứng dụng có lời giải (nâng cao) Xem chi tiết
Cách tìm nguyên hàm của hàm số
A. Phương pháp giải & Ví dụ
I. NGUYÊN HÀM VÀ TÍNH CHẤT
1. Nguyên hàm
Định nghĩa: Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Định lí:
1) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x)+C, C ∈ R là họ tất cả các nguyên hàm của f(x) trên K. Ký hiệu ∫f(x)dx = F(x) + C.
2. Tính chất của nguyên hàm
Tính chất 1: (∫f(x)dx)' = f(x) và ∫f'(x)dx = f(x) + C
Tính chất 2: ∫kf(x)dx = k∫f(x)dx với k là hằng số khác 0.
Tính chất 3: ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx
3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
4. Bảng nguyên hàm của một số hàm số sơ cấp
| Nguyên hàm của hàm số sơ cấp | Nguyên hàm của hàm số hợp (u = u(x) |
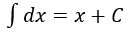
|
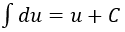
|
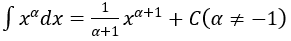
|
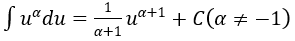
|
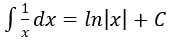
|
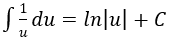
|
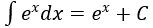
|
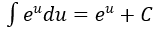
|
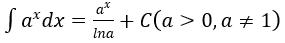
|
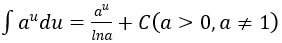
|
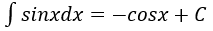
|
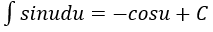
|
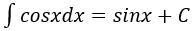
|
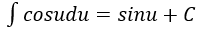
|
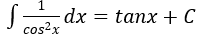
|
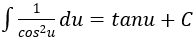
|
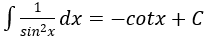
|
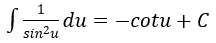
|
II. PHƯƠNG PHÁP TÍNH NGUYÊN HÀM
Phương pháp dùng định nghĩa vá tính chất
+ Biến đổi các hàm số dưới dấu nguyên hàm về dạng tổng, hiệu của các biểu thức chứa x.
+ Đưa các mỗi biểu thức chứa x về dạng cơ bản có trong bảng nguyên hàm.
+ Áp dụng các công thức nguyên hàm trong bảng nguyên hàm cơ bản.
Ví dụ minh họa
Bài 1: Tìm nguyên hàm của hàm số
Hướng dẫn:
Bài 2: Tìm nguyên hàm của hàm số
Hướng dẫn:
Bài 3: Tìm nguyên hàm của hàm số
Hướng dẫn:
Cách tìm nguyên hàm của hàm số hữu tỉ
A. Phương pháp giải & Ví dụ
Bài toán tổng quát: Tính nguyên hàm 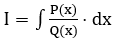
Phương pháp giải:
Nếu bậc của tử số P(x)≥ bậc của mẫu số Q(x) 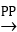
Nếu bậc của tử số P(x) < bậc của mẫu số Q(x) 
+ Nếu mẫu số phân tích được thành tích số, ta sẽ sử dụng đồng nhất thức để đưa về dạng tổng của các phân số.
Một số trường hợp đồng nhất thức thường gặp:
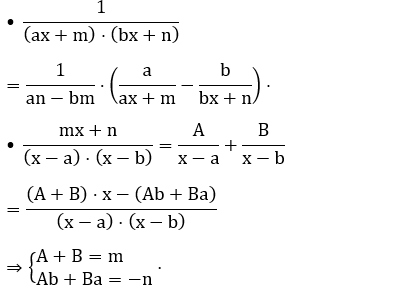
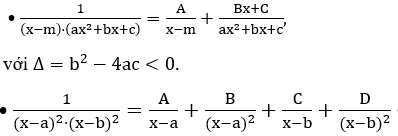
+ Nếu mẫu số không phân tích được thành tích số (biến đổi và đưa về dạng lượng giác).
Ví dụ minh họa
Bài 1: Tìm nguyên hàm F(x) của hàm số
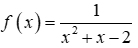
Hướng dẫn:
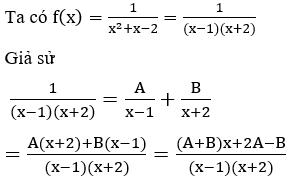
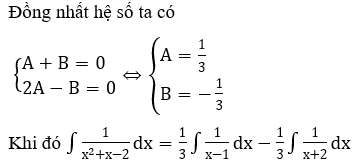
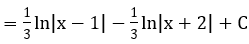
Bài 2: Tìm nguyên hàm F(x) của hàm số
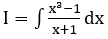
Hướng dẫn:
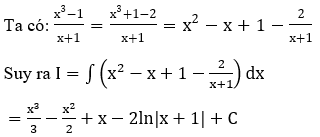
Bài 3: Tìm nguyên hàm F(x) của hàm số
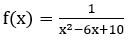
Hướng dẫn:
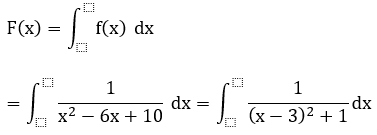
Đặt x-3 = tant ⇒ dx = (tan2 t+1)dt và t = arctan(x-3)
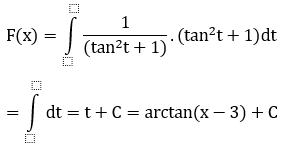
Cách tìm nguyên hàm thỏa mãn điều kiện cho trước
A. Phương pháp giải & Ví dụ
• Bước 1: Tìm nguyên hàm dựa vào những phương pháp đã biết:
♦ Sử dụng bảng nguyên hàm.
♦ Đổi biến số
♦ Nguyên hàm từng phần
♦ …
• Bước 2: Dựa vào yêu cầu của bài toán tìm ra hằng số C tương ứng.
• Bước 3: Kết luận một nguyên hàm vừa tìm được.
Ví dụ minh họa
Bài 1: Tìm một nguyên hàm F(x) của hàm số f(x)=(4x+1) ex thỏa mãn điều kiện F(1)=e.
Hướng dẫn:
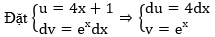
⇒ ∫(4x+1) ex dx = (4x+1) ex - ∫4ex dx = (4x+1) ex - 4ex + C = (4x-3) ex + C
Mà F(1) = e ⇒ C = 0 nên F(x) = (4x-3) ex
Bài 2: Nếu F(x) là một nguyên hàm của hàm số 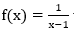
Hướng dẫn:
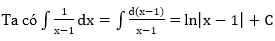
Vì F(2)=1 nên C=1. Suy ra F(x) = ln|x-1|+1, từ đó F(3) = 1+ln2.
Bài 3: Biết F(x) là một nguyên hàm của f(x)=xsin2x và thỏa F(0)+F(π) = -π/2. Tính F(π/4)
Hướng dẫn: