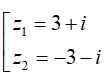Căn bậc hai của số phức và phương trình bậc hai - Toán lớp 12

Căn bậc hai của số phức và phương trình bậc hai

Với Căn bậc hai của số phức và phương trình bậc hai Toán lớp 12 tổng hợp các dạng bài tập, trên 50 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Căn bậc hai của số phức và phương trình bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

• 6 dạng bài tập Căn bậc hai, Phương trình bậc hai số phức trong đề thi Đại học có lời giải Xem chi tiết
• Dạng 1: Tìm căn bậc hai của số phức Xem chi tiết
• Dạng 2: Giải phương trình bậc 2 số phức Xem chi tiết
• Trắc nghiệm giải phương trình bậc 2 số phức Xem chi tiết

Cách tìm căn bậc hai của số phức

Phương pháp giải

Trường hợp w là số thực: Nếu a là một số thực

+a < 0 ; a có các căn bậc hai là .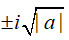

+ a = 0, a có đúng một căn bậc hai là 0.

+a > 0, acó hai căn bậc hai là .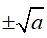

Trường hợp w = a + bi;a, b ∈ R; b ≠ 0

Gọi z = x + yi là một căn bậc hai của w khi và chỉ khi z² = w, tức là

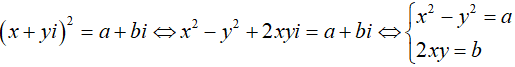
Mỗi cặp số thực (x; y) nghiệm đúng hệ phương trình trên cho ta một căn bậc hai x + y.i của số phức w = a + bi.

Ví dụ minh họa

Ví dụ 1:Tìm các căn bậc hai của w = -5 + 12i.

Hướng dẫn:

Gọi z = x + yi là một căn bậc hai của số phức w = -5 + 12i

Ta có z² = w <=> (x + yi)² = -5 + 12i

<=>

Vậy số phức w có hai căn bậc hai là 2 + 3i và -2 - 3i.

Ví dụ 2:Khai căn bậc hai số phức z = -3 + 4i có kết quả:

Hướng dẫn:

Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.

Ta có:

w² = z <=> (x + yi)² = -3 + 4i

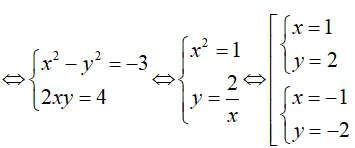
Do đó z có hai căn bậc hai là:

z₁ = 1 + 2i

z₂ = -1 - 2i

Ví dụ 3:Tính căn bậc hai của số phức z = 8 + 6i ra kết quả:

Hướng dẫn:

Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.

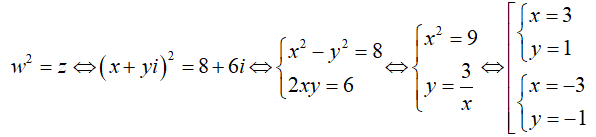
Ta có:

Do đó z có hai căn bậc hai là

Chọn đáp án A.

Cách giải phương trình bậc 2 số phức

A. Phương pháp giải & Ví dụ

- Giải các phương trình bậc hai với hệ số thực

Cho phương trình bậc hai ax² + bx + c = 0( a;b;c ∈ R;a ≠ 0).

Xét Δ = b² - 4ac, ta có

+ Δ = 0 phương trình có nghiệm thực x = .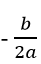

+ Δ > 0 : phương trình có hai nghiệm thực được xác định bởi công thức:

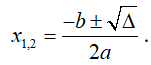
+ Δ < 0 : phương trình có hai nghiệm phức được xác định bởi công thức:

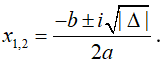
+ Chú ý.

Mọi phương trình bậc n: 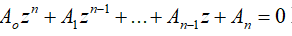luôn có n nghiệm phức (không nhất thiết phân biệt).

Hệ thức Vi–ét đối với phương trình bậc hai với hệ số thực: Cho phương trình bậc hai ax² + bx + c = 0( a; b;c ∈ R;a ≠ 0 có hai nghiệm phân biệt x₁;x₂ (thực hoặc phức).

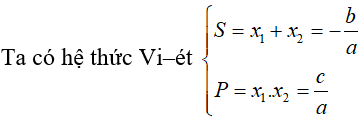
- Phương trình quy về phương trình bậc hai với hệ số thực

Phương pháp 1: Phân tích đa thức thành nhân tử:

– Bước 1: Nhẩm 1 nghiệm đặc biệt của phương trình.

+ Tổng các hệ số trong phương trình là 0 thì phương trình có một nghiệm x = 1.

+ Tổng các hệ số biến bậc chẵn bằng tổng các hệ số biến bậc lẻ thì phương trình có một nghiệm x= -1.

– Bước 2: Đưa phương trình về phương trình bậc nhất hoặc bậc hai bằng cách hân tích đa thức ở vế trái của phương trình thành nhân tử (dùng hẳng đảng thức, chia đa thức hoặc sử dụng lược đồ Hoocne) như sau:

Với đa thức f(x) = a_nxⁿ + a_{n - 1}x^{n - 1} + .... + a₁x + a_o chia cho x - a có thương là

g(x) = b_nxⁿ + b_{n - 2}x^{n - 2} + .... + b₁x + b_o dư r

Ví dụ minh họa

– Bước 3: Giải phương trình bậc nhất hoặc bậc hai, kết luận nghiệm

Phương pháp 2: Đặt ẩn phụ:

– Bước 1: Phân tích phương trình thành các đại lượng có dạng giống nhau.

– Bước 2: Đặt ẩn phụ, nêu điều kiện của ẩn phụ (nếu có).

– Bước 3: Đưa phương trình ban đầu về phương trình bậc nhất, bậc hai với ẩn mới.

– Bước 4: Giải phương trình, kết luận nghiệm.

Ví dụ 1:Giải phương trình bậc hai sau: z² - z + 1 = 0

Hướng dẫn:

Ta có a = 1 ; b = -1 ; c = 1 nên Δ = b² - 4ac = -3 < 0

Phương trình có hai nghiệm phức phân biệt là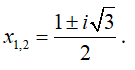

Ví dụ 2:Trong C , nghiệm của phương trình z² + √5 = 0 là:

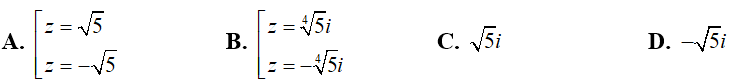
Hướng dẫn:

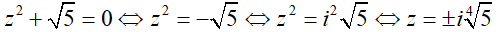
Chọn đáp án B

Ví dụ 3:Trong C , nghiệm của phương trình z³ - 8 = 0 là :

Hướng dẫn:

Sử dụng hằng đẳng thức số 7, ta có:

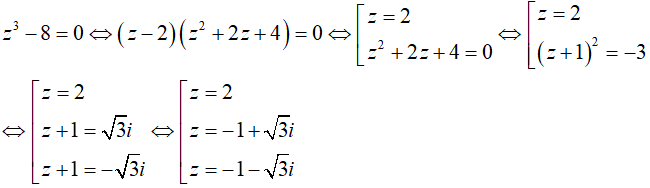
Vậy phương trình đã cho có 3 nghiệm phân biệt.

Ví dụ 4:Trong C , phương trình z² + 3iz + 4 = 0 có nghiệm là:

Hướng dẫn:

Ta có : a = 1 ; b = i ; c = 4 nên :

Δ = b² - 4ac = (3i)² - 4.1.4 = -25 <0

Phương trình có hai nghiệm phức là:

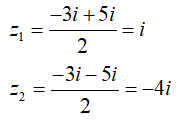
Chọn đáp án A.