Top 50 bài tập Khái niệm về thể tích của khối đa diện (mới nhất)
Haylamdo biên soạn và sưu tầm 50 bài tập Khái niệm về thể tích của khối đa diện Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Bài tập Khái niệm về thể tích của khối đa diện
Câu 1:
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng a/4. Thể tích của hình chóp S.ABC là:
A.
B.
C.
D.
Câu 2:
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.
A.
B.
C.
D.
Câu 3:
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.
A.
B.
C.
D.
Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4/3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
A.
B.
C.
D.
Câu 5:
Cho tứ diện ABCD, có các cạnh DA, DB, DC đôi một vuông góc với nhau. Biết rằng DA = a, DB = a, DC = 2a. Tính diện tích S của tam giác ABC.
A.
B.
C.
D.
Câu 6:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng a. Mặt phẳng (P) qua A và vuông góc với SC cắt SB, SC, SD lần lượt tại E, I, F. Tính tỉ số k giữa thể tích hình chóp S.AEIF và thể tích hình chóp S.ABCD.
A.
B.
C.
D.
Câu 7:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, hình chiếu của S lên đáy trùng với trung điểm của AB. Tính thể tích V của hình chóp đã cho, biết rằng AB = a, BC = a, khoảng cách từ A đến mặt (SCD) bằng a/3
A.
B.
C.
D.
Câu 8:
Cho hình chóp S.ABCD, có đáy là hình vuông cạnh a, SCD là tam giác đều và (SCD) vuông góc với đáy. Tính khoảng cách h từ A đến mặt phẳng (SBD).
A.
B.
C.
D.
Câu 9:
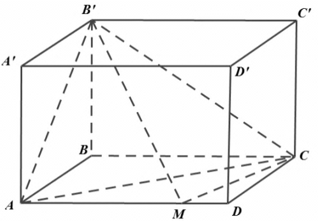
Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm của các cạnh A’A, C’C. Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Tính tỉ số giữa thể tích hình chóp D’.DMN và thể tích hình hộp ABCD.A'B'C'D'
A.
B.
C.
D.
Câu 10:
Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm các cạnh A’A, C’C. Mặt phẳng (D’EF) chia hình hộp thành hai hình đa diện. Gọi (H) là hình đa diện chứa đỉnh A, (H’) là hình đa diện còn lại. Tính tỉ số k giữa thể tích hình (H) và thể tích hình (H’).
A.
B.
C.
D.
Câu 11:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa mặt bên và mặt đáy bằng . Tính theo a thể tích khối chóp S.ABCD

A.
B.
C.
D.
Câu 12:
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60°. Tính thể tích V của hình chóp S.ABC.
A.
B.
C.
D.
Câu 13:
Hình chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích khối chóp đó bằng:
A.
B.
C.
D.
Câu 14:
Cho tứ diện ABCD có các cạnh BA, BC, BD đôi một vuông góc với nhau: BA = BC = 3a, BD = 2a. Gọi M và N lần lượt là trung điểm của AB và AD Tính thể tích khối chóp C.BDNM.
A.
B.
C.
D.
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2a. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
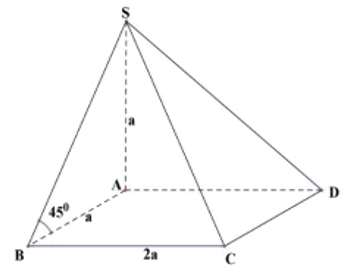
A.
B.
C.
D.
Câu 16:
Cho hình chóp tam giác đều đáy có cạnh bằng a, góc tạo bởi các mặt bên và đáy bằng 60°. Thể tích khối chóp là:
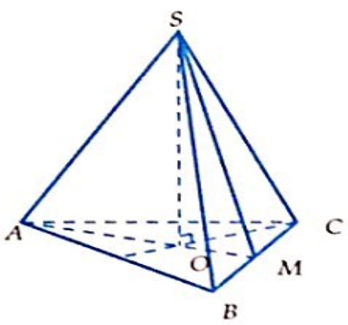
A.
B.
C.
D.
Câu 17:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = , SA vuông góc với mp đáy. Góc tạo bởi (SBC) và mặt đáy bằng 30°. Thể tích S.ABC bằng

A.
B.
C.
D.
Câu 18:
Cho khối chóp S.ABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm A', B', C' sao cho ![]() . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số
. Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S'.A'B'C'. Khi đó tỷ số ![]() là:
là:
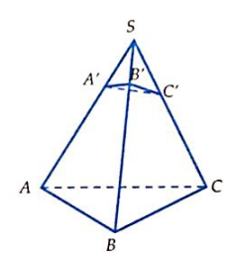
A. 12
B. 24
C.
D.
Câu 19:
Cho lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60° AB = a. Khi đó thể tích của khối ABCC'B' bằng:
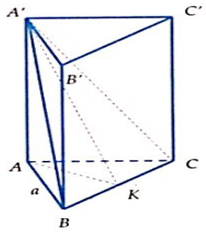
A.
B.
C.
D.
Câu 20:
Tính thể tích V của khối hộp chữ nhật ABCD.A'B'C'D', biết AB = a, AD = a và AC' hợp với đáy một góc 60°.
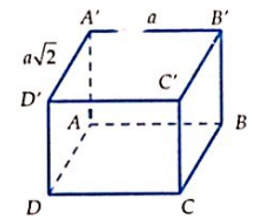
A.
B.
C.
D.
Câu 21:
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a và . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chóp S.ABCD.
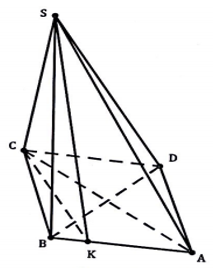
A.
B.
C.
D.
Câu 22:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, biết góc giữa cạnh bên và mặt đáy bằng 45°. Tính thể tích V của khối chóp S.ABCD.
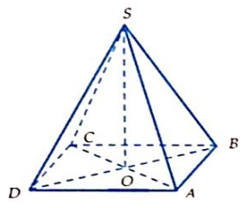
A.
B.
C.
D.
Câu 23:
Một hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng b. Thể tích của khối chóp đó là:
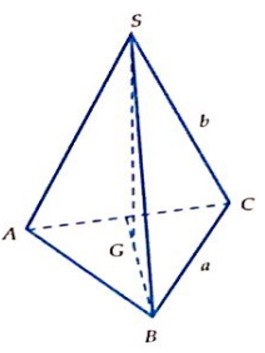
A.
B.
C.
D.
Câu 24:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, cạnh bên SC tạo với mặt phẳng (SAB) một góc 30°. Thể tích của khối chóp đó bằng:
A.
B.
C.
D.
Câu 25:
Cho khối chóp S.ABC với SA ⊥ SB , SB ⊥ SC , SC ⊥SA . Biết độ dài SA, SB, SC lần lượt là 3, 5, 6. Thể tích của khối chóp đó bằng:
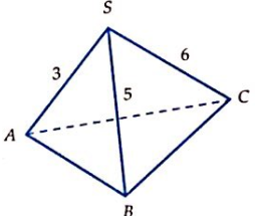
A. 20
B. 10
C. 15
D. 30
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a; mặt bên SAB nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông cân tại S. Tính thể tích V của khối chóp S.ABC.
A.
B.
C.
D.
Câu 27:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a và SA vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK.

A.
B.
C.
D.
Câu 28:
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a; SA ⊥ (ABCD), góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
A.
B.
C.
D.
Câu 29:
Cho hình chóp S.ABC có đáy là tam giác đều. Nếu tăng độ dài cạnh đáy lên 2 lần và độ dài đường cao không đổi thì thể tích S.ABC tăng lên bao nhiêu lần?
A. 4.
B. 2.
C. 3.
D. 1/2.
Câu 30:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết ΔSAB là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng (ABC). Tính thể tích khối chóp S.ABC biết AB = a, AC = a.
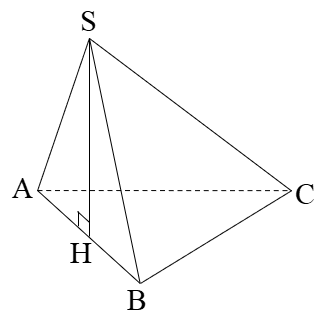
A.
B.
C.
D.
Câu 31:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a, AC = a.
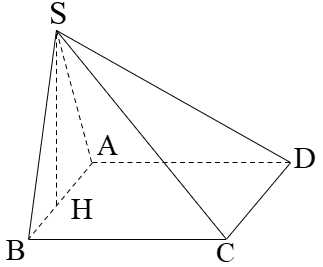
A.
B.
C.
D.
Câu 32:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Tính thể tích khối chóp S.ABC biết AB = a, AC = a, SB = a.

A.
B.
C.
D.
Câu 33:
Cho hình chóp S.ABCD có đáy ABCD hình vuông cạnh a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AD. Tính thể tích khối chóp S.ABCD biết SB = 3a/2.

A.
B.
C.
D.
Câu 34:
Hình chóp S.ABCD đáy là hình vuông cạnh a, SD = a/2. Hình chiếu của S lên (ABCD) là trung điểm H của AB. Thể tích khối chóp là
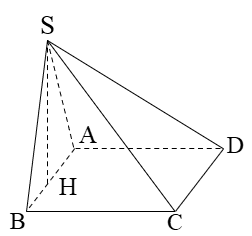
A.
B.
C.
D.
Câu 35:
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a, SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:

A.
B.
C.
D.
Câu 36:
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a, SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
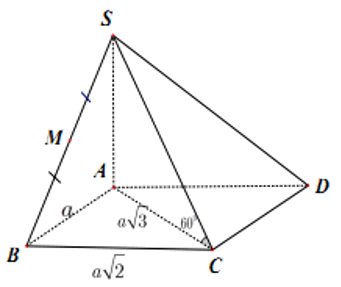
A.
B.
C.
D.
Câu 37:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a, cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng
A.
B.
C.
D.
Câu 38:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC cân tại A. Cạnh bên SB lần lượt tạo với mặt phẳng đáy, mặt phẳng trung trực của BC các góc bằng 30° và 45°, khoảng cách từ S đến cạnh BC bằng a. Tính thể tích khối chóp S.ABC
A.
B.
C.
D.
Câu 39:
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
A.
B.
C.
D.
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

A.
B.
C.
D.
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=AD=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.
A.
B.
C.
D.
Câu 3:
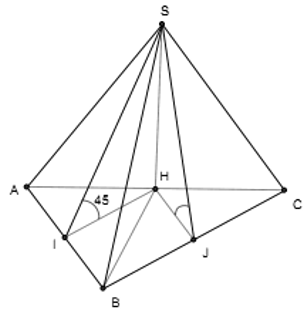
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng
A.
B.
C.
D.
Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 30°, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

A.
B.
C.
D.
Câu 5:
Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.

A.
B.
C.
D.
Câu 6:
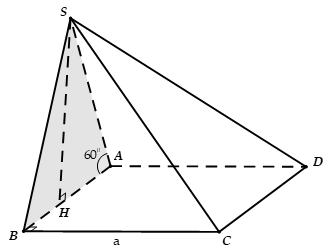
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
A.
B.
C.
D.
Câu 7:
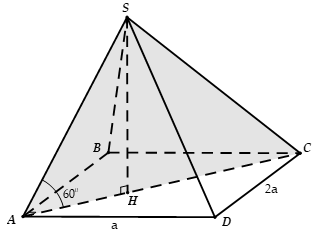
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
A.
B.
C.
D.
Câu 8:
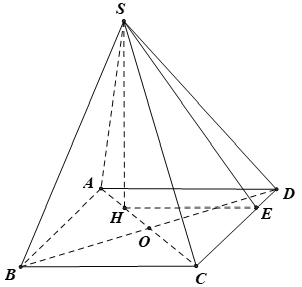
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm đoạn OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60°. Tính thể tích V của hình chóp S.ABCD
A.
B.
C.
D.
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1, góc = 60°, cạnh bên SD = . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Tính thể tích khối chóp S.ABCD.
A.
B.
C.
D.
Câu 10:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Câu 11:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và (SAB) hợp với đáy một góc 45°. Tính thể tích V của khối chóp S.ABC
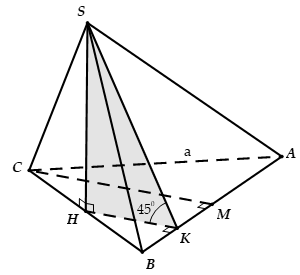
A.
B.
C.
D.
Câu 12:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.
A.
B.
C. 2
D.
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt (SAC) là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a. Tính thể tích khối chóp S.ABCD.

A.
B.
C.
D.
Câu 14:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC = a; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:
A.
B.
C.
D.
Câu 15:
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:
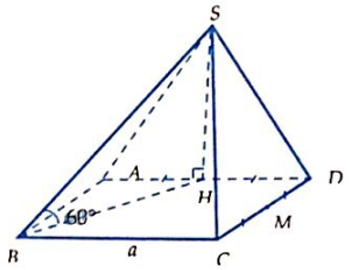
A.
B.
C.
D.
Câu 16:
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, = 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.
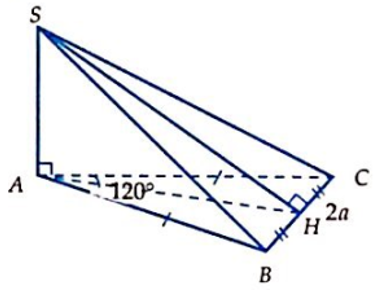
A.
B.
C.
D.
Câu 17:
Một lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều ABC cạnh a. Cạnh bên bằng b và hợp với mặt đáy góc 60°. Thể tích hình chóp A'.BCC'B' bằng bao nhiêu?

A.
B.
C.
D.
Câu 18:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , SB hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC
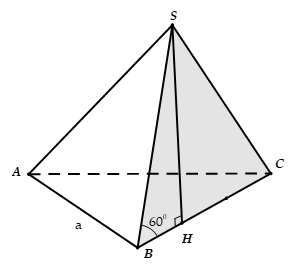
A.
B.
C.
D.
Câu 19:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Câu 20:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho , (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

A.
B.
C.
D.
Câu 21:
Cho hình chóp S.ABC có các cạnh SA = 1, SB = 2, SC = 3, AB = , BC = CA = . Tính thể tích V khối chóp S.ABC.
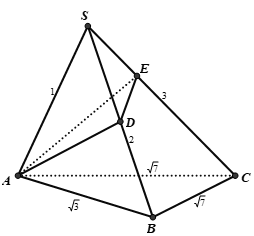
A.
B.
C.
D.
Câu 22:
Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:
A.
B.
C.
D.
Câu 23:
Gọi V là thể tích của hình lập phương ABCD.A'B'C'D'. là thể tích của tứ diện A'ABD. Hệ thức nào sau đây là đúng?
A. V = 6
B. V = 4
C. V = 3
D. V = 2
Câu 24:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC) một góc 45°. Thể tích lăng trụ là:

A.
B.
C.
D.
Câu 25:
Cho khối lăng trụ tam giác đều ABC. có tất cả các cạnh bằng a. Gọi M là trung điểm của . Thể tích khối chóp M.BC là:
A.
B.
C.
D.
Câu 26:
Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Gọi N, I lần lượt là trung điểm của AB, BC; góc giữa hai mặt phẳng (C’AI) và (ABC) bằng 60°. Tính theo a thể tích khối chóp NAC’I?
A.
B.
C.
D.
Câu 27:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a và (A’BC) hợp với mặt đáy (ABC) một góc 30°. Tính thể tích hình chóp A’.ABC là
A.
B.
C.
D.
Câu 28:
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính theo a thể tích lăng trụ ABC.A’B’C’.

A.
B.
C.
D.
Câu 29:
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 3a, BC = a, mặt bên (A’BC) hợp với mặt đáy (ABC) một góc 60°. Tính thể tích khối lăng trụ.

A.
B.
C.
D.
Câu 30:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.
A.
B.
C.
D.
Câu 31:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a; BC = 2a; AA’= a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính thể tích khối chóp M.AB’C.
A.
B.
C.
D.
Câu 32:
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A’BCD’) bằng . Tính thể tích hình hộp theo a.

A.
B.
C.
D.
Câu 33:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, = 60° và SA vuông góc với (ABCD). Biết thể tích của khối chóp S.ABCD bằng . Tính khoảng cách (k) từ A đến mặt phẳng (SBC).

A.
B.
C.
C.
Câu 34:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC.
A.
B.
C.
D.
Câu 35:
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích khối lăng trụ bằng:
A.
B.
C.
D.
Câu 36:
Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a; BC = 3a, = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:
A.
B.
C.
D.
Câu 37:
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích của khối lăng trụ ABC.A’B’C’ bằng:
A.
B.
C.
D.
Câu 38:
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:

A.
B.
C.
D.
Câu 39:
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên tạo với mặt phẳng đáy một góc bằng 45°. Hình chiếu của A trên mặt phẳng (A’B’C’) trùng với trung điểm của A’B’. Tính thể tích V của khối lăng trụ theo a.
A.
B.
C.
D.
Câu 40:
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12
B. V = 3
C. V = 9
D. V = 6
Câu 1:
Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
A.
B.
C.
D.
Câu 2:
Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V’. Khi đó:
A.
B.
C.
D.
Câu 3:
Cho khối chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi đó:
A.
B.
C.
D.
Câu 4:
Nếu một khối lăng trụ đứng có diện tích đáy bằng B và cạnh bên bằng h thì có thể tích là:
A.
B. 3Bh
C.Bh
D.
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=3a và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng:
A.
B.
C.
D.
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, . Thể tích khối chóp:
A.
B.
C.
D.
Câu 7:
Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
A. V = S.a
B.
C.
D.
Câu 8:
Nếu khối chóp OABC thỏa mãn OA=a, OB=b, OC=c và thì có thể tích là:
A. abc
B.
C.
D.
Câu 9:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a, AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
A.
B.
C.
D.
Câu 11:
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng:
A.
B.
C.
D.
Câu 12:
Nếu một khối chóp có thể tích bằng và diện tích mặt đáy bằng thì chiều cao của khối chóp bằng:
A. 2a
B. 3a
C.
D. a
Câu 13:
Cho khối chóp có chiều cao bằng 6, diện tích đáy bằng 4. Thể tích khối chóp đã cho bằng:
A. 24
B. 10
C. 12
D. 8
Câu 14:
Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là:
A.
B.
C.
D.
Câu 15:
Cho khối lăng trụ có chiều cao h = 5 và diện tích đáy S = 6. Thể tích của khối lăng trụ đã cho là:
A. 15
B. 30
C. 11
D. 10
Câu 1:
Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có dộ dài là a. Thể tích khối tứ diện S.BCD bằng:
A.
B.
C.
D.
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SC = 3a và SC vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABC bằng:
A.
B.
C.
D.
Câu 4:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết SA=BC=a, thể tích khối chóp S.ABC bằng:
A.
B.
C.
D.
Câu 5:
Mệnh đề nào dưới đây sai?
A. Hai khối hộp chữ nhật có diện tích bằng nhau thì có thể tích bằng nhau.
B. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
C. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau.
D. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau.
Câu 6:
Cho khối chóp S.ABCD có thể tích bằng , đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD. Biết diện tích tam giác SAB bằng . Tính khoảng cách từ M tới mặt phẳng (SAB)
A. 12a
B. 6a
C. 3a
D. 4a
Câu 7:
Cho hình lập phương ABCD.A'B'C'D' có diện tích mặt chéo ACC’A’ bằng . Thể tích của khối lập phương ABCD.A’B’C’D’ bằng:
A.
B.
C.
D.
Câu 8:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết . Thể tích khối chóp S.ABC là:
A.
B.
C.
D.
Câu 9:
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng . Thể tích khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 10:
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại A, . Tam giác SBC đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC
A.
B.
C.
D.
Câu 11:
Cho tứ diện ABCD có thể tích bằng 18. Gọi là trọng tâm của tam giác BCD; (P) là mặt phẳng qua A sao cho góc giữa (P) và mặt phẳng (BCD) bằng . Các đường thẳng qua B, C, D song song với cắt (P) lần lượt tại . Thể tích khối tứ diện bằng?
A.
B. 18
C.
D. 12
Câu 12:
Cho khối chóp S.ABC có các góc phẳng ở đỉnh S bằng , . Thể tích của khối chóp S.ABC bằng:
A.
B.
C.
D.
Câu 13:
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng . Thể tích của khối lăng trụ?
A.
B.
C.
D.
Câu 14:
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
A.
B.
C.
D.
Câu 15:
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
A. 50
B.
C.
D.
Câu 1:
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Gọi M, N, P, Q, E, F lần lượt là tâm các hình bình hành ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, DAA’D’. Thể tích khối đa diện có các đỉnh M, P, Q, E, F, N bằng:
A.
B.
C.
D.
Câu 2:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân tại C, . Thể tích khối lăng trụ ABC.A’B’C’ bằng:
A.
B.
C.
D.
Câu 3:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, , cạnh BC = a, đường chéo A’B tạo với mặt phẳng (ABC) một góc . Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
B.
C.
D.
Câu 4:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy một góc . Thể tích của khối chóp đó là:
A. 16
B.
C.
D.
Câu 5:
Cho hình chóp S.ABCD đáy là hình chữ nhật, SA vuông góc với đáy, . Góc giữa SB và đáy bằng . Thể tích khối chóp S.ABC bằng:
A.
B.
C.
D.
Câu 6:
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là a, 2a, 3a có thể tích lớn nhất bằng:
A.
B.
C.
D.
Câu 7:
Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn và . Thể tích khối chóp S.BCD là:
A.
B.
C.
D.
Câu 8:
Cho hình chóp đều S.ABCD có cạnh bên và cạnh đáy bằng a. Thể tích của khối chóp S.ABCD là
A.
B.
C.
D.
Câu 9:
Tính thể tích khối chóp tam giác đều có độ dài cạnh bên bằng và độ dài cạnh đáy bằng a.
A.
B.
C.
D.
Câu 10:
Cho hình chóp S.ABCD có . Biết , cạnh SC tạo với đáy một góc và diện tích tứ giác ABCD là . Gọi H là hình chiếu của A trên cạnh SC. Tính thể tích khối chóp H.ABCD.
A.
B.
C.
D.
Câu 11:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng . Tính thể tích khối chóp S.ABC?
A.
B.
C.
D.
Câu 12:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và . Điểm M thuộc cạnh SA sao cho . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A.
B.
C.
D.
Câu 13:
Cho hình lăng trụ ABC.A’B’C’ có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C trên (ABB’A’) là tâm của hình bình hành ABB’A’. Thể tích của khối lăng trụ là:
A.
B.
C.
D.
Câu 14:
Cho tứ diện đều ABCD có cạnh bằng 8. Ở bốn đỉnh tứ diện, người ta cắt đi các tứ diện đều bằng nhau có cạnh bằng x, biết khối đa diện tạo thành sau khi cắt có thể tích bằng thể tích tứ diện ABCD. Giá trị của x là:
A.
B.
C.
D.
Câu 15:
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứ BG và cắt AC, AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là:
A.
B.
C.
D.
Câu 1:
Khối lăng trụ đáy là hình chữ nhật có hai kích thước lần lượt là 2a, 3a, chiều cao khối lăng trụ là 5a. Tính thể tích khối lăng trụ:
A.
B.
C.
D.
Câu 2:
Thể tích của khối hộp chữ nhật có ba kích thước lần lượt là 1, 2, 3 bằng:
A. 2
B. 3
C. 1
D. 6
Câu 3:
Khối hộp chữ nhật có các kích thước lần lượt là a, 2a, 3a có thể tích bằng:
A.
B.
C.
D.
Câu 4:
Cho khối lăng trụ tam giác có thể tích V. Trên đáy A’B’C’ lấy điểm M bất kì. Thể tích khối chóp M.ABC tính theo V bằng:
A.
B.
C.
D.
Câu 5:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. . Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
B.
C.
D.
Câu 6:
Cho khối lập phương có thể tích bằng 27, diện tích toàn phần của khối lập phương đã cho bằng:
A. 75
B. 36
C. 18
D. 54
Câu 7:
Cho khối chóp tứ giác đều có cạnh đáy bằng a, chiều cao bằng . Thể tích khối chóp đã cho bằng:
A.
B.
C.
D.
Câu 8:
Cho hình chóp S.ABC có đáy ABC vuông tại A và SB vuông góc với đáy. Biết SB = a, SC hợp với (SAB) một góc và (SAC) hợp với đáy (ABC) một góc . Thể tích của khối chóp là:
A.
B.
C.
D.
Câu 9:
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, . Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:
A.
B.
C.
D.
Câu 10:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với đáy góc . Gọi M, N lần lượt là trung điểm của AB và AD. Thể tích của khối chóp S.MCDN là:
A.
B.
C.
D.
Câu 11:
Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng a. Gọi M là trung diểm của . Thể tích khối chóp là:
A.
B.
C.
D.
Câu 12:
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. gọi M là trung điểm cạnh BB’, điểm N thuộc cạnh CC’ sao cho CN=2C'N. Tính thể tích khối chóp A.BCNM theo V
A.
B.
C.
D.
Câu 13:
Cho hình chóp đều S.ABCD có diện tích đáy là , diện tích một mặt bên là . Thể tích khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 14:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc . Thể tích khối chóp S.ABC là:
A.
B.
C.
D.
Câu 15:
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng . Thể tích hình chóp là:
A.
B.
C.
D.
Câu 16:
Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng . Tính thể tích của khối chóp S.ABCD theo h và
A.
B.
C.
D.
Câu 18:
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a. Khoảng cách giữa hai đường thẳng SA và CD bằng . Thể tích khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 19:
Cho hình chóp đều S.ABC, góc giữa mặt bên và mặt phẳng đáy (ABC) bằng , khoảng cách giữa hai đường thẳng SA và BC bằng . Thể tích của khối chóp S.ABC theo a bằng:
A.
B.
C.
D.
Câu 20:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh bên SA=SB=SC. Góc giữa mặt phẳng (SAB) và mặt đáy bằng . Biết rằng khoảng cách giữa hai đường thẳng BC và SA bằng , khi đó thể tích khối chóp S.ABC bằng:
A.
B.
C.
D.
Câu 1:
Cho tứ diện SABC và G là trọng tâm của tứ diện, mặt phẳng quay quanh AG và cắt các cạnh SB, SC tương ứng tại M, N. Giá trị nhỏ nhất của tỉ số là
A.
B.
C.
D.
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng , góc giữa SD và đáy bằng với . Tính thể tích khối chóp đã cho.
A.
B.
C.
D.
Câu 4:
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và có thể tích . Tìm số r > 0 sao cho tồn tại điểm J nằm trong khối chóp mà khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r?
A.
B.
C.
D.
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Điểm I thuộc đoạn SA. Biết mặt phẳng (MNI) chia khối chóp S.ABCD thành hai phần, phần chứa đỉnh S có thể tích bằng lần phần còn lại. Tính tỉ số ?
A.
B.
C.
D.
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng . Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng . Tính thể tích nhỏ nhất của khối chóp S.ABC
A. 3
B.
C.
D. 4
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song với BC, . Gọi E, F là hai điểm lần lượt nằm trên các cạnh AB và AD sao cho (E, F không trùng với A). Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỉ số thể tích hai khối chóp S.BCDFE và S.ABCD là:
A.
B.
C.
D.
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, . Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng . Thể tích khối chóp đó bằng:
A.
B.
C.
D.
Câu 9:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 2, và tam giác SBD vuông cân tại S. Gọi E là trung điểm của SC. Mặt phẳng (P) qua AE và cắt hai cạnh SB, SD lần lượt tại M và N. Thể tích lớn nhất của khối đa diện ABCDNEM bằng:
A.
B.
C.
D.
Câu 10:
Cho tứ diện ABCD có , tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD) trùng với trực tâm H của tam giác BCD, mặt phẳng (ADH) tạo với mặt phẳng (ACD) một góc . Tính thể tích khối tứ diện ABCD.
A.
B.
C.
D.
Câu 11:
Khối chóp có đáy là hình bình hành, một cạnh đáy bằng a và các cạnh bên đều bằng . Thể tích của khối chóp có giá trị lớn nhất là:
A.
B.
C.
D.
Câu 12:
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên bằng . Xét điểm M thay đổi trên mặt phẳng SCD sao cho tổng nhỏ nhất. Gọi là thể tích của khối chóp S.ABCD và là thể tích của khối chóp M.ACD. Tỉ số bằng:
A.
B.
C.
D.
Câu 13:
Cho hình chóp S.ABCD có ABCD là hình chữ nhật, . M là trung điểm của AB, tam giác SMC vuông tại S, , SM tạo với đáy góc . Thể tích của khối chóp S.ABCD là:
A.
B.
C.
D.
Câu 14:
Cho hình chóp S.ABC, đáy là tam giác ABC có , hình chiếu của S lên mặt phẳng (ABC) là trung điểm O của cạnh AC. Khoảng cách từ A đến mặt phẳng (SBC) bằng 2. Mặt phẳng (SBC) hợp với mặt phẳng (ABC) một góc thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp S.ABC bằng , trong đó , a là số nguyên tố. Tổng a + b bằng:
A. 6
B. 5
C. 7
D. 4
Câu 16:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh B, . Gọi M, N, E lần lượt là trung điểm AC, BC, AB. Trên cạnh SB lấy điểm F sao cho . Thể tích khối tứ diện MNEF bằng:
A.
B.
C.
D.
Câu 17:
Cho hình hộp ABCD.A'B'C'D'. Gọi lần lượt là thể tích của khối tứ diện ACB’D’ và khối hộp ABCD.A'B'C'D'. Tỉ số bằng:
A.
B.
C.
D.
Câu 18:
Cho lăng trụ xiên tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, biết cạnh bên là và hợp với đáy ABC một góc . Thể tích khối lăng trụ là:
A.
B.
C.
D.
Câu 19:
Cho hình lăng trụ có đáy ABCD là hình thoi cạnh a và góc . Chân đường cao hạ từ B’ xuống (ABCD) trùng với giao điểm 2 đường chéo, biết BB'=a. Thể tích khối lăng trụ là:
A.
B.
C.
D.
Câu 20:
Cho hình lăng trụ ABC.A’B’C’ có . Hình chiếu vuông góc của C’ lên (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a?
A.
B.
C.
D.
Câu 1:
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A’ trên mặt phẳng (ABCD) là trung điểm I của cạnh AB. Biết A’C tạo với mặt phẳng đáy một góc với . Thể tích khối chóp A'.ICD là:
A.
B.
C.
D.
Câu 2:
Cho khối lăng trụ tam giác ABC.A’B’C’ mà mặt bên ABB’A’ có diện tích bằng 4. Khoảng cách giữa CC’ và mặt phẳng (ABB’A’) bằng 7. Thể tích khối lăng trụ là:
A. 10
B. 12
C. 14
D. 16
Câu 3:
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a và . Thể tích khối lăng trụ ABC.A’B’C’ theo a là:
A.
B.
C.
D.
Câu 4:
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân và AB’ vuông góc với (A’B’C’). Mặt phẳng (AA’C’) tạo với mặt phẳng (A’B’C’) một góc . Thể tích khối lăng trụ ABC.A’B’C’ là:
A.
B.
C.
D.
Câu 5:
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC. Cho . Thể tích của khối lăng trụ đã cho là:
A.
B.
C.
D.
Câu 6:
Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với . Hai mặt bên (ABB’A’) và (ADD’A’) lần lượt tạo với đáy những góc và . Tính thể tích khối hộp nếu biết cạnh bên bằng 1.
A. V = 3
B. V = 2
C. V = 4
D. V = 8
Câu 7:
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh , , hình chiếu vuông góc của B trên mặt phẳng (A’B’C’D’) trùng với trung điểm của A’C’. Gọi là góc tạo bởi hai mặt phẳng (ABCD) và (CDD’C’), . Thể tích của khối hộp ABCD.A’B’C’D’ bằng:
A.
B.
C.
D.
Câu 8:
Cho hình lăng trụ xiên ABC.A’B’C’ có đáy ABC là tam giác đều với tâm O. Hình chiếu của C’ trên (ABC) là O. Tính thể tích của lăng trụ biết rằng khoảng cách từ O đến CC’ là a và 2 mặt bên (ACC’A’) và (BCC’B’) hợp với nhau góc
A.
B.
C.
D.
Câu 9:
Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc . Gọi M là trung điểm của cạnh BC và I là trung điểm của AM. Biết rằng hình chiếu của điểm I lên mặt đáy A’B’C’ là trọng tâm G của tam giác A’B’C’. Thể tích khối lăng trụ là:
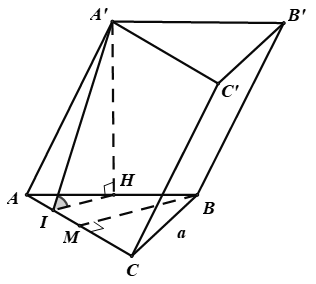
A.
B.
C.
D.
Câu 10:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cân tại A. . Mặt phẳng (AB’C’) tạo với đáy một góc . Thể tích khối lăng trụ là:
A.
B.
C.
D.
Câu 11:
Lăng trụ tam giác đều ABC.A’B’C’ có góc giữa hai mặt phẳng (A’BC) và (ABC) bằng . Điểm M nằm trên cạnh AA’. Biết cạnh , thể tích khối đa diện MBCC’B’ bằng:
A.
B.
C.
D.
Câu 12:
Đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a=4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ?
A. 8
B.
C.
D.
Câu 13:
Cho lăng trụ ABC.A’B’C’ với ABC là tam giác vuông cân tại C có AB = a mặt bên ABB’A’ là hình vuông. Mặt phẳng qua trung điểm I của AB và vuông góc với AB’ chia khối lăng trụ thành 2 phần. Tính thể tích mõi phần?
A.
B.
C.
D.
Câu 14:
Cho khối lăng trụ ABC.A'B'C' có thể tích bằng 1. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AA’ và BB’. Đường thẳng CM cắt đường thẳng C’A’ tại P, đường thẳng CN cắt đường thẳng C’B’ tại Q. Thể tích của khối đa diện lồi A’MPB’NQ bằng:
A. 1
B.
C.
D.
Câu 15:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B với . Gọi M là trung điểm của A’C’, I là giao điểm cuẩ đường thẳng AM và A’C. Tính theo a thể tích khối IABC.
A.
B.
C.
D.
Câu 16:
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Cạnh . Biết tứ giác BCC’B’ là hình thoi có nhọn. Mặt phẳng (BCC’B’) vuông góc với (ABC) và mặt phẳng (ABB’A’) tạo với (ABC) góc . Thể tích khối lăng trụ ABC.A’B’C’ bằng:
A.
B.
C.
D.
Câu 17:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB = a, đường thẳng A’B tạo với mặt phẳng (BCC’B’) một góc . Tính thể tích khối lăng trụ ABC.A’B’C’
A.
B.
C.
D.
Câu 18:
Cho hình lập phương ABCD.A’B’C’D’ có thể tích V. Gọi M là điểm thuộc cạnh BB’ sao cho . Mặt phẳng đi qua M và vuông góc với AC’ cắt các cạnh DD’, DC, BC lần lượt tại N, P, Q. Gọi là thể tích của khối đa diện CPQMNC’. Tính tỉ số
A.
B.
C.
D.
Câu 19:
Cho lăng trụ đều ABC.A’B’C’, cạnh đáy bằng a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng . Tính thể tích khối lăng trụ đó.
A.
B.
C.
D.
Câu 20:
Cho hình chóp đều S.ABC, góc giữa mặt bên và mặt phẳng đáy (ABC) bằng , khoảng cách giữa hai đường thẳng SA và BC bằng . Thể tích của khối chóp S.ABC theo a bằng:
A.
B.
C.
D.
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và Tính thể tích V của khối chóp S.ABCD
A.
Câu 2:
Cho hình chóp S.ABC có tam giác SBC là tam giác vuông cân tại S, và khoảng cách từ A đến mặt phẳng bằng Tính theo a thể tích V của khối chóp S.ABC
A. .
Câu 3:
Cho khối chóp S.ABC có SA vuông góc với đáy, và . Tính thể tích V của khối chóp S.ABC.
A.
Câu 4:
A. .
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và . Tính theo a thể tích V khối chóp S.ABCD
A. .
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và . Cạnh bên và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp S.ABC.
A.
Câu 7:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, . Cạnh bên và vuông góc với đáy. Tính thể tích khối chóp S.ABCD.
A. .
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có . Mặt bên là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng . Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 9:
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 10:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
A.
Câu 11:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng . Tính theo a thể tích V của khối chóp đã cho.
A. .
Câu 12:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a và thể tích bằng . Tính chiều cao h của hình chóp đã cho.
A.
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB= a. Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Tính theo a thể tích V của khối chóp S.ABC
A. .
Câu 14:
A. .
Câu 15:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Hình chiếu vuông góc của S trên AB là điểm H thỏa . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 16:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Cạnh bên SA vuông góc với đáy, góc . Tính thể tích V của khối chóp S.ABCD.
Câu 17:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, , . Tam giác SAC vuông tại S và nằm trong mặt phẳng vuông góc với đáy . Tính theo a thể tích V của khối chóp .
A. .
Câu 18:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Cạnh bên và vuông góc với đáy; diện tích tam giác SBC bằng (đvdt). Tính theo a thể tích V của khối chóp S.ABCD.
Câu 19:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C, cạnh huyền AB bằng 3. Hình chiếu vuông góc của S xuống mặt đáy trùng với trọng tâm của tam giác ABC và . Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 20:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với . Đường thẳng SA vuông góc với mặt đáy, cạnh bên SB tạo với mặt đáy một góc . Tính theo a thể tích V của khối chóp .
A. .
Câu 22:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng ; góc giữa đường thẳng SB và mặt phẳng bằng . Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 23:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Cạnh bên SA vuông góc với đáy và SD tạo với đáy một góc . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 24:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1. Hình chiếu vuông góc của S trên mặt phẳng là trung điểm H của cạnh AB, góc giữa SC và mặt đáy bằng . Tính thể tích V của khối chóp S.ABCD.
A. .
Câu 25:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với . Đỉnh S cách đều các điểm Biết góc giữa đường thẳng SB và mặt phẳng bằng Tính theo a thể tích V của khối chóp S.ABCD
A. .
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, . Cạnh bên SA vuông góc với đáy . Gọi I là trung điểm của BC, SI tạo với mặt phẳng góc Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 27:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng bằng . Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 28:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; đỉnh S cách đều các điểm Biết ; góc giữa đường thẳng SB và mặt đáy bằng . Tính theo a thể tích V của khối chóp S.ABC.
A. .
Câu 29:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD=1. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng . Tính thể tích khối chóp S.ABCD.
A. .
Câu 30:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng trùng với trọng tâm của tam giác ABC. Đường thẳng SD hợp với mặt phẳng góc . Tính theo a thể tích V của khối chóp S.ABCD
A. .
Câu 31:
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với cạnh đáy AD và BC, Cạnh bên SA vuông góc với mặt phẳng và SD tạo với mặt phẳng góc . Tính thể tích V của khối chóp đã cho.
A. .
Câu 32:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S. Hình chiếu vuông góc của S trên mặt đáy là điểm H thuộc cạnh AD sao cho . Biết rằng và SC tạo với đáy một góc bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 33:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy và . Gọi N là trung điểm SD, đường thẳng AN hợp với đáy một góc . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 34:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy, SD tạo với mặt phẳng một góc bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A.
Câu 35:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng , tam giác SBC vuông tại S và nằm trong mặt phẳng vuông góc với đáy, đường thẳng SD tạo với mặt phẳng một góc . Tính thể tích V của khối chóp S.ABCD.
A. .
Câu 36:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên với mặt đáy bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 37:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc đáy và mặt bên hợp với đáy một góc bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 38:
Câu 39:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng và mặt phẳng bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 40:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, đường chéo AC=a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa và đáy bằng . Tính theo a thể tích V của khối chóp S.ABCD.
A. .
Câu 41:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, ; cạnh bên SA vuông góc với đáy; mặt phẳng tạo với mặt đáy một góc . Tính thể tích V của khối chóp S.ABCD.
A. .
Câu 42:
Cho tứ diện ABCD có . Góc giữa hai mặt phẳng và bằng . Tính thể tích V của khối tứ diện đã cho.
A. .
Câu 43:
Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc với nhau; và Gọi tương ứng là trung điểm các cạnh Tính thể tích V của tứ diện AMNP
A.
Câu 44:
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC.
A.
Câu 45:
Câu 46:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, , SA=a và vuông góc với đáy . Gọi G là trọng tâm tam giác SBC. Mặt phẳng qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính theo a thể tích V của khối chóp S.AMN.
Câu 47:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M và N lần lượt là trung điểm của các cạnh AB và AD; H là giao điểm của CN và DM. Biết SH vuông góc với mặt phẳng và . Tính thể tích khối chóp S.CDNM.
A. .
Câu 48:
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2a. Mặt bên tạo với đáy góc . Gọi K là hình chiếu vuông góc của O trên SD. Tính theo a thể tích V của khối tứ diện DKAC.
A. .
Câu 50:
A.
Câu 1:
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a
A.
Câu 2:
Tính thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng a và tổng diện tích các mặt bên bằng
A.
Câu 3:
Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và . Tính thể tích V của khối lăng trụ đã cho.
A.
Câu 4:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác với AB=a, AC=2a, . Tính thể tích V của khối lăng trụ đã cho.
A. .
Câu 6:
A. .
Câu 7:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, . Tính theo a thể tích khối hộp đã cho.
A. .
Câu 8:
Cho hình hộp chữ nhật có diện tích ba mặt cùng xuất phát từ cùng một đỉnh là Tính thể tích V của hình hộp chữ nhật đã cho.
A.
Câu 9:
Cho hình hộp chữ nhật có đường chéo Độ dài ba kích thước của hình hộp chữ nhật lập thành một cấp số nhân có công bội Thể tích của khối hộp chữ nhật là
A.
Câu 10:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B và . Cạnh A'B tạo với mặt đáy góc . Tính thể tích của khối lăng trụ đã cho.
A. .
Câu 11:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=AA'=a, đường chéo A'C hợp với mặt đáy một góc thỏa mãn . Tính theo a thể tích khối hộp đã cho.
A. .
Câu 12:
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với mặt phẳng tạo với đáy một góc Tính thể tích V của khối lăng trụ đã cho.
A.
Câu 13:
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân, AB=a và , góc giữa mặt phẳng và mặt đáy bằng . Tính theo a thể tích khối lăng trụ.
Câu 14:
Tính theo a thể tích V của khối hộp chữ nhật ABCD.A'B'C'D'. Biết rằng mặt phẳng hợp với đáy một góc , A'C hợp với đáy một góc và .
A. .
Câu 15:
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh bằng 1, . Góc giữa đường thẳng AC' và mặt phẳng bằng . Tính thể tích V của khối lăng trụ.
A. .
Câu 16:
Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh đều bằng 2a, đáy ABCD là hình vuông. Hình chiếu vuông góc của đỉnh A' trên mặt phẳng đáy trùng với tâm của đáy. Tính theo a thể tích V của khối hộp đã cho.
A. .
Câu 17:
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a, cạnh bên AA'=a , hình chiếu vuông góc của A' trên mặt phẳng trùng với trung điểm H của AB . Tính theo a thể tích V của khối lăng trụ đã cho.
A. .
Câu 18:
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC=2a. Hình chiếu vuông góc của A' trên mặt phẳng là trung điểm H của cạnh AB và . Tính thể tích V của khối lăng trụ đã cho.
A. .
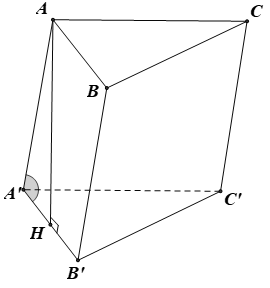
Câu 19:
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết . Tính thể tích V của khối lăng trụ đã cho.
A. .
Câu 20:
Cho hình lăng trụ S.ABCD có đáy là tam giác đều cạnh và . Hình chiếu vuông góc của điểm A' trên mặt phẳng trùng với trọng tâm G của tam giác BC. Tính thể tích V của khối lăng trụ đã cho.
A. .
Câu 21:
Tính thể tích V của khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, . Biết rằng .
A. .
Câu 22:
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=1; AC=2 cạnh bên . Hình chiếu vuông góc của A' trên mặt đáy trùng với chân đường cao hạ từ B của tam giác ABC. Tính thể tích V của khối lăng trụ đã cho.
A. .
Câu 23:
Tính thể tích V của khối lăng trụ ABC.A'B'C' biết thể tích khối chóp A.BCB'C' bằng
A.
Câu 24:
Cho hình hộp ABCD.A'B'C'D' có thể tích bằng Tính thể tích V của khối tứ diện AB'CD'
A.
Câu 25:
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật tâm O và AB=a, ; A'O vuông góc với đáy . Cạnh bên AA' hợp với mặt đáy một góc . Tính theo a thể tích V của khối lăng trụ đã cho.
A. .
Câu 26:
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông góc của A' lên mặt phẳng trùng với trung điểm H của BC. Góc tạo bởi cạnh bên AA' với mặt đáy là . Tính thể tích khối trụ ABC.A'B'C'.
A. .
Câu 27:
Cho hình lăng trụ tam giác ABC có đáy ABC là tam giác vuông cân tại A, cạnh . Biết AC' tạo với mặt phẳng một góc và . Tính thể tích V của khối đa diện .
A.
Câu 28:
A.
Câu 29:
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và . Góc giữa cạnh bên AA' và mặt đáy bằng . Đỉnh A' cách đều các điểm . Tính theo a thể tích V của khối lăng trụ đã cho.
A. .
Câu 30:
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O cạnh a góc . Biết rằng và cạnh bên hợp với đáy một góc bằng Tính thể tích V của khối đa diện
A.

