Top 50 bài tập Ứng dụng của tích phân trong hình học (mới nhất)

Câu 1:

Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục Ox và hai đường thẳng x = a, x = b (a < b) quanh trục Ox

A. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}$

B. $V={\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{f}}^2\left(\mathrm{x}\right)\mathrm{dx}$

C. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{dx}$

D. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{f}}^2\left(\mathrm{x}\right)\mathrm{dx}$

Xem lời giải »

Câu 2:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^3-x$ và đồ thị hàm số $y=x-x^2$

A. $\frac{9}{4}$

B. $\frac{37}{12}$

C. $\frac{81}{12}$

D. 13

Xem lời giải »

Câu 3:

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số $y=(x-1)e^{2x}$, trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox

A. $V=\frac{\mathrm{\pi }}{2}\left(e^4-13\right)$

B. $V=\frac{\mathrm{\pi }}{32}\left(e^4+4\right)$

C. $V=\frac{\mathrm{\pi }}{32}\left(e^4-11\right)$

D. $V=\frac{\mathrm{\pi }}{32}\left(e^4-5\right)$

Xem lời giải »

Câu 4:

Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Có bao nhiêu trẻ được sinh trong khoảng thời gian này ( tức là trong 10 năm đầu tiên sau chiến tranh)?

A. 100 triệu     

B. 120 triệu     

C. 150 triệu     

D. 250 triệu

Xem lời giải »

Câu 5:

Sau chiến tranh thế giới thứ hai, tốc độ sinh ở cả nước phương Tây tăng rất nhanh. Giả sử rằng tốc độ sinh được cho bởi: b(t) = 5 + 2t, 0 ≤ t ≤ 10 , ( ở đó t số năm tính từ khi chiến tranh kết thúc, b(t) tính theo đơn vị triệu người). Tìm khoảng thời gian T sao cho số lượng trẻ được sinh ra là 14 triệu kể từ khi kết thức chiến tranh.

A. 1 năm

B. 2 năm

C. 3 năm

D. 4 năm

Xem lời giải »

Câu 6:

Diện tích hình phẳng giới hạn bởi $y=x^2-x+3$ và $y = 2x + 1$ là:

A. $\frac{3}{2}$

B. $-\frac{3}{2}$

C. $\frac{1}{6}$

D. $-\frac{1}{6}$

Xem lời giải »

Câu 7:

Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là: 

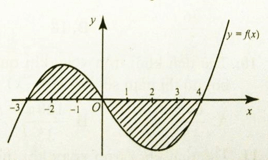
A. ${\int }_{-3}^{4}f\left(x\right)dx$

B. ${\int }_{-3}^{1}f\left(x\right)dx+{\int }_1^{4}f\left(x\right)dx$

C. ${\int }_{-3}^{0}f\left(x\right)dx+{\int }_0^4\left[-f\left(x\right)\right]dx$

D. ${\int }_{-3}^{0}f\left(x\right)dx+{\int }_0^{4}f\left(x\right)dx$

Xem lời giải »

Câu 8:

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x +\frac{1}{x}$, trục hoành, đường thẳng x = -1 và đường thẳng x = -2 là:

A. $\ln 2+\frac{3}{2}$

B. $\ln 2+\frac{11}{3}$

C. $\ln 2+\frac{19}{3}$

D. $\ln 2+\frac{5}{2}$

Xem lời giải »

Câu 9:

Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y=\sqrt{x}$ và y = 6 - x và trục tung là

A. $\frac{22}{3}$

B. $\frac{11}{3}$

C. $\frac{19}{3}$

D. $\frac{25}{3}$

Xem lời giải »

Câu 10:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = e^x - e^{-x }$, trục hoành, đường thẳng x = -1 và đường thẳng x = 1.

A. $e+\frac{1}{e}-2$

B. 0

C. $2\left(e+\frac{1}{e}-2\right)$

D. $e+\frac{1}{e}$

Xem lời giải »

Câu 11:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = \sqrt{x} - x$ và trục hoành.

A. 1

B. $\frac{1}{6}$

C. $\frac{5}{6}$

D. $\frac{1}{3}$

Xem lời giải »

Câu 12:

Gọi h(t) (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng $h\text{'}\left(t\right)=\frac{1}{5}\sqrt[3]{t+8}$ và lúc đầu bồn không có nước. Mức nước ở bồn sau khi bơm nước được 6 giây xấp xỉ bằng: 

A. 2,65cm     

B. 2,66cm     

C. 2,67cm     

D. 2,68cm.

Xem lời giải »

Câu 13:

Vận tốc của một vật chuyển động là $v\left(t\right) = \frac{1}{2\mathrm{\pi }} + \frac{\sin \left(\mathrm{\pi }t\right) }{\mathrm{\pi }}$ (m/s). Quãng đường vật di chuyển trong khoảng thời gian 1,5 giây xấp xỉ bằng:

A. 0,33m     

B. 0,34m     

C. 0,35m     

D. 0,36m

Xem lời giải »

Câu 14:

Thể tích phần vật thể giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và $2\sqrt{(9-x^2)}$

A. $\frac{\sqrt{6}}{3}$

B. 18

C. $\frac{2\sqrt{3}}{3}$

D. $\frac{3\sqrt{3}}{3}$

Xem lời giải »

Câu 15:

Thể tích khối xoay khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số y = x(x-4) và trục hoành là:

A. $\frac{64\mathrm{\pi }}{15}$

B. $\frac{128\mathrm{\pi }}{15}$

C. $\frac{256\mathrm{\pi }}{15}$

D. $\frac{512\mathrm{\pi }}{15}$

Xem lời giải »

Câu 16:

Thể tích khối tròn khi quay quanh trục hoành một hình phẳng giới hạn bởi đồ thị hàm số $y = \sin x\cos x, y = 0, x = 0, x = \frac{\pi }{2}$ là:

A. $\frac{{\mathrm{\pi }}^2}{4}$

B. $\frac{{\mathrm{\pi }}^2}{8}$

C. $\frac{{\mathrm{\pi }}^2}{16}$

D. $\frac{{\mathrm{\pi }}^2}{32}$

Xem lời giải »

Câu 17:

Thể tích khối tròn xoay khi quay quanh trục tung một hình phẳng giới hạn bởi hình tròn tâm I(2;0) bán kính R = 1 là:

A. ${\pi }^2$

B. $2{\pi }^2$

C. $4{\pi }^2$

D. $8{\pi }^2$

Xem lời giải »

Câu 1:

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), đường thẳng y = 0 và hai đường thẳng x = a, x = b (a < b) là:

A. $S={\int }_a^{b}f\left(x\right)dx$

B. $S={\int }_0^{b}f\left(x\right)dx$

C. $S={\int }_b^a\left|f\left(x\right)\right|dx$

D. $S={\int }_a^b\left|f\left(x\right)\right|dx$ 

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) liên tục trên [a; b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức

A. $S=\mathrm{\pi }{\int }_a^b{\left[f\left(x\right)\right]}^{2}dx$

B. $S={\int }_a^b\left|f\left(x\right)\right|dx$

C. $S=\mathrm{\pi }{\int }_a^b\left|f\left(x\right)\right|dx$

D. $S={\int }_b^a\left|f\left(x\right)\right|dx$ 

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) liên tục trên [a; b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b) là:

A. $S={\int }_b^a\left|f\left(x\right)\right|dx$ 

B. $S={\int }_a^{b}f\left(x\right)dx$

C. $S={\int }_a^b\left|f\left(x\right)\right|dx$

D. $S={\int }_b^{a}f\left(x\right)dx$ 

Xem lời giải »

Câu 4:

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left(x\right)=x^2-1$ trục hoành và hai đường thẳng x = −1; x = −3 là:

A. $S={\int }_{-3}^{-1}\left|x^2-1\right|dx$

B. $S={\int }_{-1}^{-3}\left|x^2-1\right|dx$

C. $S={\int }_{-3}^0\left|x^2-1\right|dx$

D. $S={\int }_{-3}^{-1}\left(1-x^2\right)dx$  

Xem lời giải »

Câu 5:

Hình phẳng giới hạn bởi đồ thị hàm số y = f(x) liên tục trên đoạn [1;3], trục Ox và hai đường thẳng x = 1, x = 3 có diện tích là:

A. $S={\int }_1^{3}f\left(x\right)dx$

B. $S={\int }_1^3\left|f\left(x\right)\right|dx$

C. $S={\int }_3^{1}f\left(x\right)dx$

D. $S={\int }_3^1\left|f\left(x\right)\right|dx$ 

Xem lời giải »

Câu 6:

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b (a < b) là:

A. $S={\int }_a^b\left(f\left(x\right)-g\left(x\right)\right)dx$

B. $S={\int }_a^b\left(g\left(x\right)-f\left(x\right)\right)dx$

C. $S={\int }_a^b\left|f\left(x\right)-g\left(x\right)\right|dx$

D. $S={\int }_a^b\left|f\left(x\right)\right|dx-{\int }_a^{b}g\left(x\right)dx$ 

Xem lời giải »

Câu 7:

Cho hàm số y = f(x), y = g(x) liên tục trên [a; b]. Gọi (H) là hình phẳng giới hạn bởi hai đồ thị y = f(x), y = g(x) và các đường thẳng x = a, x = b. Diện tích (H) được tính theo công thức?

A. $S_H={\int }_a^b\left|f\left(x\right)\right|dx-{\int }_a^b\left|g\left(x\right)\right|dx$

B. $S_H={\int }_a^b\left|f\left(x\right)-g\left(x\right)\right|dx$

C. $S_H=\left|{\int }_a^b\left[f\left(x\right)-g\left(x\right)\right]dx\right|$

D. $S_H={\int }_a^b\left[f\left(x\right)-g\left(x\right)\right]dx$ 

Xem lời giải »

Câu 8:

Cho hai hàm số $f\left(x\right) = -x$ và $g\left(x\right)=e^x$. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = 0, x = e là:

A. $S={\int }_0^e\left|e^x+x\right|dx$

B. $S={\int }_0^e\left|e^x-x\right|dx$

C. $S={\int }_e^0\left|e^x-x\right|dx$

D. $S={\int }_e^0\left|e^x+x\right|dx$ 

Xem lời giải »

Câu 9:

Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x = π, đồ thị hàm số y = cosx và trục Ox là

A. $S={\int }_0^{\mathrm{\pi }}\cos xdx$

B. $S={\int }_0^{\mathrm{\pi }}{\cos }^{2}xdx$

C. $S={\int }_0^{\mathrm{\pi }}\left|\cos x\right|dx$

D. $S=\mathrm{\pi }{\int }_0^{\mathrm{\pi }}\left|\cos x\right|dx$  

Xem lời giải »

Câu 10:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=x^3$, trục hoành và hai đường thẳng x = 1; x = 3?

A. 19

B. $\frac{2186}{7}\mathrm{\pi }$

C. 20

D. 18

Xem lời giải »

Câu 11:

Cho hình (H) giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b. thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Ox là:

A. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{dx}$

B. $V={\int }_{\mathrm{a}}^{\mathrm{b}}\left|\mathrm{f}\left(\mathrm{x}\right)\right|\mathrm{dx}$

C. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{f}}^2\left(\mathrm{x}\right)\mathrm{dx}$

D. $V={\mathrm{\pi }}^2{\int }_{\mathrm{a}}^{\mathrm{b}}{\mathrm{f}}^2\left(\mathrm{x}\right)\mathrm{dx}$ 

Xem lời giải »

Câu 12:

Cho hình (H) giới hạn bởi đồ thị hàm số $y=x^3$, trục hoành và hai đường thẳng x = 0, x = 1. Thể tích khối tròn xoay tạo thành khi quay (H)  quanh trục Ox được tính bởi:

A. $V={\mathrm{\pi }}^2{\int }_0^1{\mathrm{x}}^3\mathrm{dx}$

B. $V=\mathrm{\pi }{\int }_0^1{\mathrm{x}}^3\mathrm{dx}$

C. $V=\mathrm{\pi }{\int }_0^1{\mathrm{x}}^6\mathrm{dx}$

D. $V=\mathrm{\pi }{\int }_0^1{\mathrm{x}}^5\mathrm{dx}$  

Xem lời giải »

Câu 13:

Gọi (D) là hình phẳng giới hạn bởi các đường $y=2^x,y=0,x=0,x=2$. Thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục Ox được xác định bởi công thức:

A. $V=\mathrm{\pi }{\int }_0^2{2}^{\mathrm{x}+1}\mathrm{dx}$

B. $V={\int }_0^2{2}^{\mathrm{x}+1}\mathrm{dx}$

C. $V={\int }_0^2{4}^{\mathrm{x}}\mathrm{dx}$

D. $V=\mathrm{\pi }{\int }_0^2{4}^{\mathrm{x}}\mathrm{dx}$ 

Xem lời giải »

Câu 14:

Cho hàm số y = f (x) liên tục trên đoạn (a;b) và $f\left(x\right)>0 \forall x\in (a;b)$. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoảnh và 2 đường thẳng x = a, x = b (a < b). Thể tích vật thể tròn xoay khi quay D quanh Ox được tính theo công thức:

A. ${\int }_a^b\mathrm{f}\left({\mathrm{x}}^2\right)\mathrm{dx}$

B. $\mathrm{\pi }{\int }_a^b\mathrm{f}\left({\mathrm{x}}^2\right)\mathrm{dx}$

C. $\mathrm{\pi }{\int }_a^b{\left(\mathrm{f}\left(\mathrm{x}\right)\right)}^2\mathrm{dx}$

D. ${\int }_a^b{\left(\mathrm{f}\left(\mathrm{x}\right)\right)}^2\mathrm{dx}$ 

Xem lời giải »

Câu 15:

Cho hàm số y = f (x) liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức:

A. $\mathrm{V}={\mathrm{\pi }}^2{\int }_1^3{\left[\mathrm{f}\left(\mathrm{x}\right)\right]}^2\mathrm{dx}$

B. $\mathrm{V}={\int }_1^3{\left[\mathrm{f}\left(\mathrm{x}\right)\right]}^2\mathrm{dx}$

C. $\mathrm{V}=\frac{1}{3}{\int }_1^3{\left[\mathrm{f}\left(\mathrm{x}\right)\right]}^2\mathrm{dx}$

D. $\mathrm{V}=\mathrm{\pi }{\int }_1^3{\left[\mathrm{f}\left(\mathrm{x}\right)\right]}^2\mathrm{dx}$ 

Xem lời giải »

Câu 1:

Diện tích S của hình phẳng giới hạn bởi các đường $y = 2x, x = -3, x = -2$ và trục hoành được tính bằng công thức nào dưới đây?

A. $S={\int }_{-2}^{-3}2xdx$

B. $S=\mathrm{\pi }{\int }_{-2}^{-3}4x^{2}dx$

C. $S={\int }_{-3}^{-2}2xdx$

D. $S={\int }_{-3}^{-2}{\left(2x\right)}^{2}dx$ 

Xem lời giải »

Câu 2:

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y=x^3–x;y=2x$ và các đường thẳng x = −1; x = 1 được xác định bởi công thức:

A. $S=\left|{\int }_{-1}^1\left(3x-x^3\right)dx\right|$

B. $S={\int }_{-1}^0\left(3x-x^3\right)dx+{\int }_0^1\left(x^3-3x\right)dx$

C. $S={\int }_{-1}^1\left(3x-x^3\right)dx$

D. $S={\int }_{-1}^0\left(x^3-3x\right)dx+{\int }_0^1\left(3x-x^3\right)dx$  

Xem lời giải »

Câu 3:

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số $y=e^x$, trục hoành, hai đường thẳng x = −2; x = 3 có công thức tính là

A. $S={\int }_{-2}^{3}x{e}^{x}dx$

B. $S={\int }_{-2}^3\left|x{e}^x\right|dx$

C. $S=\left|{\int }_{-2}^{3}x{e}^{x}dx\right|$

D. $S=\mathrm{\pi }{\int }_{-2}^{3}x{e}^{x}dx$ 

Xem lời giải »

Câu 4:

Cho hình phẳng (H) giới hạn bởi đồ thị hàm số $y=x^3-4x$, trục hoành, đường thẳng x = −2 và đường thẳng x = 1. Diện tích của hình phẳng (H) bằng

A. $\frac{25}{4}$

B. $\frac{11}{2}$

C. $\frac{23}{4}$

D. $\frac{21}{4}$ 

Xem lời giải »

Câu 5:

Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường y = f(x), trục hoành và hai đường thẳng x = −1, x = 2 (như hình vẽ). Đặt $a={\int }_{-1}^{0}f\left(x\right)dx, b={\int }_0^{2}f\left(x\right)dx$. Mệnh đề nào sau đây đúng?

A. S = b-a

B. S = b+a

C. S = -b+a

D. S = -b-a

Xem lời giải »

Câu 6:

Cho hàm số y = f(x) liên tục trên đoạn [a; b] và cắt trục hoành tại điểm x = c (a < c < b) (như hình vẽ bên). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b. Mệnh đề nào dưới đây đúng?

A. $S={\int }_a^{c}f\left(x\right)dx-{\int }_c^{b}f\left(x\right)dx$

B. $S=-{\int }_a^{c}f\left(x\right)dx+{\int }_c^{b}f\left(x\right)dx$

C. $S={\int }_a^{c}f\left(x\right)dx+{\int }_c^{b}f\left(x\right)dx$

D. $S={\int }_a^{b}f\left(x\right)dx$ 

Xem lời giải »

Câu 7:

Cho hàm số y = f(x). Xác định công thức tính diện tích S của hình phẳng (phần gạch chéo) trong hình:

A. $S={\int }_{-2}^{3}f\left(x\right)dx$

B. $S={\int }_0^{-2}f\left(x\right)dx+{\int }_2^{3}f\left(x\right)dx$

C. $S={\int }_0^{-2}f\left(x\right)dx+{\int }_3^{0}f\left(x\right)dx$

D. $S={\int }_0^{-2}f\left(x\right)dx+{\int }_0^{3}f\left(x\right)dx$ 

Xem lời giải »

Câu 8:

Cho hàm số $y = f_1\left(x\right)$ và $y = f_2\left(x\right)$ liên tục trên [a; b] và có đồ thị như hình bên. Gọi S là hình phẳng giới hạn bới hai đồ thị trên và các đường thẳng x = a, x = b . Mệnh đề nào sau đây đúng?

A. $S={\int }_a^b\left(f_2\left(x\right)-f_1\left(x\right)\right)dx$

B. $S={\int }_a^b{\left(f_1\left(x\right)-f_2\left(x\right)\right)}^{2}dx$

C. $S=\mathrm{\pi }{\int }_a^b\left({f_1}^2\left(x\right)-{f_2}^2\left(x\right)\right)dx$ 

D. $S={\int }_a^b\left(f_1\left(x\right)-f_2\left(x\right)\right)dx$ 

Xem lời giải »

Câu 9:

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

A. ${\int }_{-1}^2\left(2x^2-2x-4\right)dx$

B. ${\int }_{-1}^2\left(-2x+2\right)dx$

C. ${\int }_{-1}^2\left(-2x-2\right)dx$

D. ${\int }_{-1}^2\left(2x^2+2x+4\right)dx$ 

Xem lời giải »

Câu 10:

Gọi S  là diện tích hình phẳng giới hạn bởi các đường $y=x^3,y=2–x$ và $y=0$. Mệnh đề nào sau đây là đúng?

A. $S={\int }_0^1{x}^{3}dx+{\int }_1^2\left(x-2\right)dx$

B. $S=\left|{\int }_0^2\left(x^3+x-2\right)dx\right|$

C. $S=\frac{1}{2}+{\int }_0^1{x}^{3}dx$

D.  $S={\int }_0^1\left|x^3+x-2\right|dx$ 

Xem lời giải »

Câu 11:

Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau:

A. $S=\frac{8}{3}$

B. $S=\frac{10}{3}$

C. $S=\frac{7}{3}$

D. $S=\frac{11}{3}$ 

Xem lời giải »

Câu 12:

Cho hình (H) giới hạn bởi đường cong $y^2+x=0$, trục Oy và hai đường thẳng y = 0, y = 1. Thể tích khối tròn xoay tạo thành khi quay (H) quanh trục Oy được tính bởi:

A. $V={\mathrm{\pi }}^2{\int }_0^1{\mathrm{x}}^4\mathrm{dx}$

B. $V=\mathrm{\pi }{\int }_0^1{\mathrm{y}}^{2}dy$

C. $V=\mathrm{\pi }{\int }_0^1{\mathrm{y}}^{4}dy$

D. $V=\mathrm{\pi }{\int }_0^1-{\mathrm{y}}^{4}dy$ 

Xem lời giải »

Câu 13:

Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường $x=\sqrt{y}; y=-x+2; x=0$ quanh trục Ox có giá trị là kết quả nào sau đây?

A. $V=\frac{3}{2}\mathrm{\pi }$

B. $V=\frac{1}{3}\mathrm{\pi }$

C. $V=\frac{11}{6}\mathrm{\pi }$

D. $V=\frac{32}{15}\mathrm{\pi }$ 

Xem lời giải »

Câu 14:

Cho hình phẳng (H) giới hạn bởi $y=\frac{1}{3}{x}^3-x^2$ và Ox. Thể tích khối tròn xoay sinh ra khi quay (H) quanh Ox bằng

A. $\frac{81\mathrm{\pi }}{35}$

B. $\frac{53\mathrm{\pi }}{6}$

C. $\frac{81}{35}$

D. $\frac{21\mathrm{\pi }}{5}$ 

Xem lời giải »

Câu 15:

Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số $y=2(x-1)e^x$, trục tung và trục hoảnh. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox

A. V = 4-2e

B. $V = \left(4-2e\right)\mathrm{\pi }$

C. $V = e^2-5$

D. $V = \left(e^2-5\right)\mathrm{\pi }$ 

Xem lời giải »

Câu 1:

Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường  và x=4 quanh trục Ox. Đường thẳng x=a (0<a<4) cắt đồ thị hàm số $y=\sqrt{x}, y=0$ tại M. Gọi $V_1$ là thể tích khối tròn tạo thành khi quay quanh tam giác OMH quanh trục Ox. Biết rằng $V=2V_1$. Khi đó:

A. $a=2\sqrt{2}$

B. $a=\frac{5}{2}$ 

C. a = 2

D. a = 3

Xem lời giải »

Câu 2:

Thể tích khối tròn xoay thu được khi quay quanh trục Ox: hình phẳng giới hạn bởi đồ thị hàm số $y=\frac{\sqrt{3x+1}}{x+1}$, trục hoành và đường thẳng x = 1 là:

A. $\mathrm{\pi }3\ln 3$

B. $\mathrm{\pi }\left(3\ln 3-2\right)$

C. $3\ln 3-1$

D. $\mathrm{\pi }\left(3\ln 3-1\right)$ 

Xem lời giải »

Câu 3:

Một khung cửa kính hình parabol với đỉnh M và cạnh đáy AB như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là $200.000đồng /m^2$ và phần kính trắng còn lại là $150.000đồng /m^2$. Cho MN = AB = 4m và MC = CD = DN. Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?

A. 1.954.000 đồng 

B. 2.123.000 đồng 

C. 1.946.000 đồng 

D. 2.145.000 đồng 

Xem lời giải »

Câu 4:

Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số$y=x^2-4x+4,$ trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm A (0; 4) và có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.

A. k = - 8 

B. k = - 6 

C. k = - 2 

D. k = - 4 

Xem lời giải »

Câu 5:

Diện tích hình phẳng của phần tô đậm trong hình vẽ bên được tính theo công thức nào dưới đây?

A. $S={\int }_0^1\left(-4x^2+4x\right)dx$

B. $S={\int }_0^1\left(2x^2-4x+1\right)dx$

C. $S={\int }_0^1\left(4x^2-4x\right)dx$

D. $S={\int }_{-1}^1\left(-4x^2+4x\right)dx$ 

Xem lời giải »

Câu 6:

Gọi (H) là hình phẳng giới hạn bởi các đường cong $y=-x^3+12x,y=-x^2$. Diện tích của (H) bằng:

A. $\frac{343}{12}$

B. $\frac{793}{4}$

C. $\frac{397}{4}$

D. $\frac{937}{12}$ 

Xem lời giải »

Câu 7:

Diện tích hình phẳng giới hạn bởi mửa đường tròn $x^2+y^2=2,y >0$ và parabol $y=x^2$ bằng:

A. $\mathrm{\pi }+\frac{4}{3}$

B. $\frac{\mathrm{\pi }}{2}-1$

C. $\frac{\mathrm{\pi }}{2}$

D. $\frac{\mathrm{\pi }}{2}+\frac{1}{3}$ 

Xem lời giải »

Câu 8:

Diện tích hình phẳng giới hạn bởi các đồ thị $y=x^2$ và $y=|x-2|$ bằng:

A. $\frac{13}{2}$

B. $\frac{21}{2}$

C. $\frac{9}{2}$ 

D. $\frac{1}{2}$ 

Xem lời giải »

Câu 9:

Diện tích hình phẳng giới hạn với đường cong $y=4-\left|x\right|$ và trục hoành Ox là

A. 0

B. 16

C. 4

D. 8

Xem lời giải »

Câu 10:

Cho hình phẳng (H) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm A(2;4), như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng (H) khi quay xung quanh trục Ox

A. $\frac{32\mathrm{\pi }}{5}$

B. $\frac{16\mathrm{\pi }}{15}$

C. $\frac{22\mathrm{\pi }}{5}$

D. $\frac{2\mathrm{\pi }}{3}$ 

Xem lời giải »

Câu 11:

Diện tích hình phẳng giới hạn bởi các đường $\left|y\right|=1-x^2$ là:

A. $\frac{4}{3}$

B. 2

C. $\frac{8}{3}$

D. 1

Xem lời giải »

Câu 12:

Cho hàm số $y=\frac{x-m^2}{x+1}$ (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?

A. Hai

B. Ba

C. Một

D. Không

Xem lời giải »

Câu 13:

Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ

Diện tích hai phần A và B lần lượt là $\frac{16}{3}$ và $\frac{63}{4}$. Tính ${\int }_{-1}^{\frac{3}{2}}f\left(2x+1\right)dx$

A. $\frac{253}{12}$

B. $\frac{253}{24}$

C. $-\frac{125}{24}$

D. $-\frac{125}{12}$ 

Xem lời giải »

Câu 14:

Cho vật thể có mặt đáy là hình nón bán kính bằng 1 (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $\left(-1\le x\le 1\right)$ thì thiết diện là một tam giác đều. Tính thể tích V của vật thể đó.

A. $V=\sqrt{3}$

B. $V=3\sqrt{3}$

C. $V=\frac{4\sqrt{3}}{3}$

D. $V=\mathrm{\pi }$ 

Xem lời giải »

Câu 15:

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = - 1 và x = 1, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox có hoành độ x $\left(-1\le x\le 1\right)$ là một tam giác vuông cân với cạnh huyền bằng $\sqrt{1-x^4}$

A. $\frac{3}{4}$

B. $\frac{2}{5}$

C. 1

D. $\frac{1}{4}$ 

Xem lời giải »

Câu 1:

Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $\left(1\le x\le 3\right)$ thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và $\sqrt{3x^2-2}$

A. $V=32+2\sqrt{15}$

B. $V=\frac{124\mathrm{\pi }}{3}$

C. $V=\frac{124}{3}$

D. $V=\left(32+2\sqrt{15}\right)\mathrm{\pi }$ 

Xem lời giải »

Câu 2:

Thể tích vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $\left(0\le x\le 2\right)$ là một nửa đường tròn đường kính  bằng:

A. $2\mathrm{\pi }$

B. $5\mathrm{\pi }$

C. $4\mathrm{\pi }$

D. $3\mathrm{\pi }$ 

Xem lời giải »

Câu 3:

Cho hình phẳng giới hạn bởi $D=\left\{y=\tan x; y=0; x=0; x=\frac{\mathrm{\pi }}{3}\right\}$. Thể tích vật tròn xoay khi D quay quanh trục Ox là: $V=\mathrm{\pi }\left(\mathrm{a}-\frac{\mathrm{\pi }}{\mathrm{b}}\right)$ với $a,b\in R$. Tính $T=a^2+2b$

A. T = 6

B. T = 9

C. T = 12

D. T = 3

Xem lời giải »

Câu 4:

Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình $x^2+y^2=1$ và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình bên)

A. $\frac{16}{3}$

B. $\frac{14}{3}$

C. $\frac{17}{3}$

D. $\frac{13}{3}$ 

Xem lời giải »

Câu 5:

Cho hình phẳng (H) giới hạn bởi parabol$y=a{x}^2+1(a>0),$ trục tung và đường thẳng x = 1. Quay (H) quanh trục Ox được một khối tròn xoay có thể tích bằng $\frac{28}{15}\mathrm{\pi }$. Mệnh đề nào dưới đây đúng?

A. 2 < a < 3

B. 0 < a < 2

C. 5 < a < 8

D. 3 < a < 5

Xem lời giải »

Câu 6:

Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y=tanx, trục Ox, đường thẳng x = 0, đường thẳng $x=\frac{\mathrm{\pi }}{3}$ quanh trục Ox là:

A. $V=\sqrt{3}-\frac{\mathrm{\pi }}{3}$

B. $V=\sqrt{3}+\frac{\mathrm{\pi }}{3}$

C. $V=\mathrm{\pi }\sqrt{3}+\frac{{\mathrm{\pi }}^2}{3}$

D. $V=\mathrm{\pi }\sqrt{3}-\frac{{\mathrm{\pi }}^2}{3}$ 

Xem lời giải »

Câu 7:

Tính thể tích khi $S=\left\{y=x^2-4x+6 ;y=-x^2-2x+6\right\}$ quay quanh trục Ox

A. 3

B. $\frac{\mathrm{\pi }}{3}$

C. $\mathrm{\pi }$

D. $3\mathrm{\pi }$ 

Xem lời giải »

Câu 8:

Gọi H là hình phẳng giới hạn bởi parabol $y=x^2$ và đường thẳng y = 2x. Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành

A. $V=\frac{64\mathrm{\pi }}{15}$

B. $V=\frac{16\mathrm{\pi }}{15}$

C. $V=\frac{20\mathrm{\pi }}{3}$

D. $V=\frac{4\mathrm{\pi }}{3}$ 

Xem lời giải »

Câu 9:

Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b] với a < b. Kí hiệu $S_1$ là diện tích hình phẳng giới hạn bởi các đường y = 3f(x), y = 3g(x), x = a, x = b, $S_2$ là diện tích hình phẳng giới hạn bởi các đường y = f(x) − 2, y = g(x) − 2, x = a, x = b. Khẳng định nào sau đây đúng?

A. $S_1=2S_2-2$

B. $S_1=2S_2+2$

C. $S_1=2S_2$

D. $S_1=3S_2$ 

Xem lời giải »

Câu 10:

Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh Ox của hình giới hạn bởi trục Ox và parabol (P): $y=x^2–ax$ (a>0) bằng V = 2. Khẳng định nào dưới đây đúng?

A. $a\in \left(\frac{1}{2};1\right)$

B. $a\in \left(1;\frac{3}{2}\right)$

C. $a\in \left(\frac{3}{2};2\right)$

D. $a\in \left(2;\frac{5}{2}\right)$ 

Xem lời giải »

Câu 11:

Cho hai hàm số $y=f_1\left(x\right)$ và $y=f_2\left(x\right)$ liên tục trên đoạn [a;b] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x = a, x = b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây?

A. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}\left({{\mathrm{f}}_1}^2\left(\mathrm{x}\right)-{{\mathrm{f}}_2}^2\left(\mathrm{x}\right)\right)\mathrm{dx}$

B. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}\left({\mathrm{f}}_1\left(\mathrm{x}\right)-{\mathrm{f}}_2\left(\mathrm{x}\right)\right)\mathrm{dx}$

C. $V={\int }_{\mathrm{a}}^{\mathrm{b}}\left({{\mathrm{f}}_1}^2\left(\mathrm{x}\right)-{{\mathrm{f}}_2}^2\left(\mathrm{x}\right)\right)\mathrm{dx}$

D. $V=\mathrm{\pi }{\int }_{\mathrm{a}}^{\mathrm{b}}{\left({\mathrm{f}}_1\left(\mathrm{x}\right)-{\mathrm{f}}_2\left(\mathrm{x}\right)\right)}^2\mathrm{dx}$ 

Xem lời giải »

Câu 12:

Cho hai hàm số $f\left(x\right)=m{x}^3+n{x}^2+px-\frac{5}{2}$ (m, n, p thuộc R) và $g\left(x\right)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng

A. $\frac{9}{2}$

B. $\frac{18}{5}$

C. 4

D. 5

Xem lời giải »

Câu 13:

Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình $4x^2=y^4$ và $4\left(\right|x|-1{)}^3=y^2$ để tạo hoa văn cho viên gạch. Diện tích phần màu vàng gần nhất với giá trị nào dưới đây?

A. 506$\left(c{m}^2\right)$ 

B. 747$\left(c{m}^2\right)$ 

C. 507$\left(c{m}^2\right)$ 

D. 746$\left(c{m}^2\right)$ 

Xem lời giải »

Câu 14:

Cho hàm số $y=x^4-3x^2+m$ có đồ thị là $\left(C_m\right)$ (m là tham số thực). Giả sử $\left(C_m\right)$ cắt trục Ox tại 4 điểm phân biệt. Gọi $S_1, S_2$ là diện tích của hai hình phẳng nằm dưới trục Ox và $S_3$ là diện tích của hình phẳng nằm trên trục Ox được tạo bởi  $\left(C_m\right)$ với trục Ox. Biết rằng tồn tại duy nhất giá trị $m=\frac{a}{b}$ (với a, b thuộc N* và tối giản) để $S_1 + S_2 = S_3$. Giá trị của 2a − b bằng:

A. 3

B. -4

C. 6

D. -2

Xem lời giải »

Câu 15:

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là $S_1$ và $S_2$ (tham khảo hình vẽ).

Tỉ số $\frac{S_1}{S_2}$ bằng:

A. $\frac{1}{2}$

B. $\frac{3}{5}$

C. $\frac{2}{5}$

D. $\frac{1}{3}$ 

Xem lời giải »

Câu 16:

Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A, B, C, D và hai đường parabol có các đỉnh lần lượt là E, F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M, N, P, Q. Biết AB = 8m, CD = 6m, $MN = PQ = 3\sqrt{3}m$, EF = 2m. Chi phí để trồng hoa trên vườn là $300.000đ/m^2$. Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây

A. 4.477.800 đồng 

B. 4.477.000 đồng 

C. 4.477.815 đồng 

D. 4.809.142 đồng 

Xem lời giải »

Câu 17:

Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(−1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = 1 và x = −1. Mệnh đề nào sau đây là đúng?

A. $S={\int }_0^{-1}f\left(x\right)dx+{\int }_0^1\left|f\left(x\right)\right|dx$

B. $S={\int }_{-1}^1\left|f\left(x\right)\right|dx$

C. $S={\int }_{-1}^{1}f\left(x\right)dx$

D. $S=\left|{\int }_{-1}^{1}f\left(x\right)dx\right|$ 

Xem lời giải »

Câu 18:

Cho parabol (P) có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi (P) và trục hoành.

A. $\frac{8}{3}$

B. $\frac{4}{3}$ 

C. 4

D. 2

Xem lời giải »

Câu 19:

Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y=x^2-2x$ và $y=-x^2+4x$

A. 12

B. 9

C. $\frac{11}{3}$

D. 27

Xem lời giải »

Câu 20:

Tính diện tích hình phẳng giới hạn bởi hai đường: $y=|x^2-4x+3|;y=x+3$

A. $\frac{107}{6}$

B. $\frac{109}{6}$

C. $\frac{109}{7}$

D. $\frac{109}{8}$ 

Xem lời giải »

Câu 21:

Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số $y=x^2-4x+4$, trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A (0; 4) có hệ số góc k chia (H)  thành 2 phần có diện tích bằng nhau là

A. K = -6

B. K = -2

C. K = -8

D. K = -4

Xem lời giải »

Câu 22:

Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ bên thì parabol có phương trình $y=x^2$ và đường thẳng là y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vường nhỏ bằng 92.

A. $OM=2\sqrt{5}$

B. $OM=3\sqrt{10}$ 

C. OM = 15

D. OM = 10

Xem lời giải »

Câu 23:

Cho (H) là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{x}^2$, cung tròn có phương trình $y=\sqrt{4-x^2}$ (với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{4\mathrm{\pi }+\sqrt{3}}{12}$

B. $\frac{4\mathrm{\pi }-\sqrt{3}}{6}$

C. $\frac{4\mathrm{\pi }+2\sqrt{3}-3}{6}$

D. $\frac{5\sqrt{3}-2\mathrm{\pi }}{3}$ 

Xem lời giải »

Câu 24:

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=-x^2+2x+1$ và $y=2x^2-4x+1$ là:

A. 4

B. 5

C. 8

D. 10

Xem lời giải »

Câu 25:

Diện tích S của hình phẳng giới hạn bởi các đường $y=-x^2+2x,y=-3,x=1,x=2$ được tính bởi công thức nào dưới đây?

A. $S=\mathrm{\pi }{\int }_1^2{\left(-{\mathrm{x}}^2+2\mathrm{x}+3\right)}^2\mathrm{dx}$

B. $S={\int }_1^2\left(-{\mathrm{x}}^2+2\mathrm{x}-3\right)\mathrm{dx}$

C. $S={\int }_1^2\left(-{\mathrm{x}}^2+2\mathrm{x}+3\right)\mathrm{dx}$

D. $S={\int }_1^2\left({\mathrm{x}}^2-2\mathrm{x}-3\right)\mathrm{dx}$ 

Xem lời giải »

Câu 1:

Diện tích hình phẳng giới hạn bởi các đường $y=x^2–x,y=2x-2,x=0,x=3$

A. $S=\left|{\int }_0^3\left(x^2-3x+2\right)dx\right|$

B. $S={\int }_1^2\left|x^2-3x+2\right|dx$

C. $S={\int }_0^3\left|x^2-3x+2\right|dx$

D. $S={\int }_1^2\left|x^2+x-2\right|dx$ 

Xem lời giải »

Câu 2:

Tìm diện tích hình phẳng giới hạn bởi các đường $y=(x-1)e^x$, trục hoành, đường thẳng x = 0 và x = 1

A. S = 2 + e 

B. S = 2 − e 

C. S = e – 2 

D. S = e − 1 

Xem lời giải »

Câu 3:

Diện tích của hình phẳng giới hạn bởi các đường $y=x^2+1,y=0,x=-1,x=2$ bằng:

A. $\frac{10}{3}$

B. 6

C. 4

D. 14

Xem lời giải »

Câu 4:

Diện tích hình phẳng giới hạn bởi $y=x^2,y=0,x=1,x=2$ bằng

A. $\frac{4}{3}$

B. $\frac{7}{3}$

C. $\frac{8}{3}$ 

D. 1

Xem lời giải »

Câu 5:

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\frac{1}{x}$, trục hoành và các đường thẳng x = 1, x = e

A. 2

B. e

C. e-1

D. 1

Xem lời giải »

Câu 6:

Diện tích của hình phẳng giới hạn bởi các đường $y=co{s}^{2}x,y=0,x=0,x=\frac{\mathrm{\pi }}{4}$ bằng

A. $\frac{\mathrm{\pi }}{4}+1$

B. $\frac{\mathrm{\pi }}{8}+1$

C. $\frac{\mathrm{\pi }}{8}$

D. $\frac{\mathrm{\pi }}{8}+\frac{1}{4}$ 

Xem lời giải »

Câu 7:

Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số $y=x^2–4$ và y = x − 4.

A. $S=\frac{16}{3}$

B. $S=\frac{161}{6}$

C. $S=\frac{1}{6}$

D. $S=\frac{5}{6}$ 

Xem lời giải »

Câu 8:

Cho hàm số $y=f\left(x\right)=x^3-3x^2-4x\left(C\right)$. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số (C) và trục hoành. Phát biểu nào sau đây đúng?

A. $S={\int }_{-1}^0\left(x^3-3x^2-4x\right)dx+{\int }_0^4\left(x^3-3x^2-4x\right)dx$

B. $S={\int }_{-1}^4\left(x^3-3x^2-4x\right)dx$

C. $S={\int }_{-1}^0\left(x^3-3x^2-4x\right)dx-{\int }_0^4\left(x^3-3x^2-4x\right)dx$x

D. $S=\left|{\int }_{-1}^4\left(x^3-3x^2-4x\right)dx\right|$ 

Xem lời giải »

Câu 9:

Tính diện tích hình phẳng giới hạn bởi các đồ thị $y=x^2-2x$ và $y=-x^2+x$

A. 6

B. 12

C. $\frac{9}{8}$

D. $\frac{10}{3}$ 

Xem lời giải »

Câu 10:

Tính diện tích hình phẳng giới hạn bởi parabol $y=x^2-2x$ và đường thẳng y = x

A. $\frac{9}{2}$

B. $\frac{11}{6}$

C. $\frac{27}{6}$

D. $\frac{17}{6}$ 

Xem lời giải »

Câu 11:

Tính diện tích S của hình phẳng giới hạn bởi hai đường cong $y=x^3–x$ và $y=x–x^2$

A. $S=\frac{12}{37}$

B. $S=\frac{37}{12}$

C. $S=\frac{9}{4}$

D. $S=\frac{19}{6}$ 

Xem lời giải »

Câu 12:

Hình phẳng (H) có diện tích bằng S, gấp 2 lần diện tích hình phẳng được giới hạn bởi đồ thị các hàm số $y=x^2-4,y=2x-4$. Tính diện tích S?

A. $S=\sqrt{8}$

B. $S=2$

C. $S=\frac{8}{3}$

D. $S=\frac{4}{3}$ 

Xem lời giải »

Câu 13:

Cho hình phẳng (H) giới hạn bởi các đường $y=|x^2-4x+3| ;y=x+3$ (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{37}{2}$

B. $\frac{109}{6}$

C. $\frac{454}{25}$

D. $\frac{91}{5}$ 

Xem lời giải »

Câu 14:

Cho (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình $y=\frac{10}{3}x-x^2, y=\left\{\begin{array}{l}-x khi x\le 1\\ x-2 khi x>1\end{array}\right.$. Diện tích của (H) bằng?

A. $\frac{11}{6}$

B. $\frac{13}{2}$

C. $\frac{11}{2}$

D. $\frac{14}{3}$ 

Xem lời giải »

Câu 15:

Gọi S là diện tích của Ban Công của một ngôi nhà có dạng như hình vẽ (S được giới hạn bởi parabol (P) và trục Ox). Giá trị của S là:

A. $S=\frac{8}{3}$

B. S = 1

C. $S=\frac{4}{3}$ 

D. S = 2

Xem lời giải »

Câu 16:

Cho số dương a thỏa mãn điều kiện hình phẳng giới hạn bởi các đường parabol $y=a{x}^2-2$ và $y=4-2a{x}^2$ có diện tích bằng 16. Giá trị của a bằng

A. 1

B. $\frac{1}{2}$

C. $\frac{1}{4}$ 

D. 2

Xem lời giải »

Câu 17:

Ba Tí muốn làm cửa sắt được thiết kế như hình bên. Vòm cổng có hình dạng một parabol. Giá $1m^2$ cửa sắt là 660000 đồng. Cửa sắt có giá (nghìn đồng) là:

A. 6500

B. 5500

C. 5600

D. 6050

Xem lời giải »

Câu 18:

Cho đồ thị hàm số y = f(x) như hình vẽ dưới đây. Diện tích S của hình phẳng (phần gạch chéo) được xác định bởi

A. $S={\int }_{-2}^{2}f\left(x\right)dx$

B. $S={\int }_1^{-2}f\left(x\right)dx+{\int }_1^{2}f\left(x\right)dx$

C. $S={\int }_{-2}^{1}f\left(x\right)dx+{\int }_1^{2}f\left(x\right)dx$

D. $S={\int }_{-2}^{1}f\left(x\right)dx-{\int }_1^{2}f\left(x\right)dx$ 

Xem lời giải »

Câu 19:

Cho (H) là hình phẳng giới hạn bởi các đồ thị hàm số $y=e,y=e^x$ và $y = (1 - e)x + 1$ (tham khảo hình vẽ bên). Diện tích của (H) là

A. $S=\frac{e+1}{2}$

B. $S=e+\frac{1}{2}$

C. $S=e+\frac{3}{2}$

D. $S=\frac{e-1}{2}$ 

Xem lời giải »

Câu 20:

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây?

A. ${\int }_{-1}^2\left(-\frac{1}{2}{x}^4+x^2+\frac{3}{2}x+1\right)dx$

B. ${\int }_{-1}^2\left(-\frac{1}{2}{x}^4-x^2-\frac{3}{2}x-4\right)dx$

C. ${\int }_{-1}^2\left(-\frac{1}{2}{x}^4-x^2-\frac{3}{2}x-1\right)dx$

D. ${\int }_{-1}^2\left(-\frac{1}{2}{x}^4+x^2+\frac{3}{2}x+4\right)dx$ 

Xem lời giải »

Câu 21:

Diện tích hình phẳng được gạch chéo như hình vẽ bằng:

A. ${\int }_{-1}^3\left(-x^2+2x-3\right)dx$

B. ${\int }_{-1}^3\left(-x^2+2x+3\right)dx$

C. ${\int }_{-1}^3\left(x^2-2x-3\right)dx$

D. ${\int }_{-1}^3\left(x^2+2x-3\right)dx$ 

Xem lời giải »

Câu 22:

Vòm cửa lớn của một trung tâm văn hóa có hình parabol. Gắn parabol vào hệ trục Oxy thì nó có đỉnh (0; 8) và cắt trục hoành tại 2 điểm phân biệt, trong đó có 1 điểm là (−4; 0). Người ta dự định lắp vào cửa kính cho vòm cửa này. Hãy tính diện tích mặt kính cần lắp vào.

A. $\frac{128}{3}{m}^2$

B. $\frac{131}{3}{m}^2$

C. $\frac{28}{3}{m}^2$

D. $\frac{26}{3}{m}^2$ 

Xem lời giải »

Câu 23:

Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số $\frac{AB}{CD}$ bằng

A. $\frac{1}{\sqrt{2}}$

B. $\frac{4}{5}$

C. $\frac{1}{\sqrt[3]{2}}$

D. $\frac{3}{1+2\sqrt{2}}$ 

Xem lời giải »

Câu 24:

Người ta cần trồng hoa tại phần đắt nằm phía ngoài đường tròn tâm gốc tọa độ O, bán kính bằng $\frac{1}{\sqrt{2}}$ và phía trong của Elip có độ dài trục lớn bằng $2\sqrt{2}$ và độ dài trục nhỏ bằng 2 (như hình vẽ bên). Trong mỗi một đơn vị diện tích cần bón $\frac{100}{\left(2\sqrt{2}-1\right)\mathrm{\pi }}$ kg phân hữu cơ. Hỏi cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa?

A. 30kg 

B. 40kg 

C. 50kg 

D. 45kg 

Xem lời giải »

Câu 25:

Cho hàm số $y=f_1\left(x\right)$ và $y=f_2\left(x\right)$ liên tục trên [a;b] và có đồ thị như hình bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x = a, x = b. Mệnh đề nào sau đây đúng?

A. $S={\int }_a^b\left(f_2\left(x\right)-f_1\left(x\right)\right)dx$

B. $S={\int }_a^b{\left(f_1\left(x\right)-f_2\left(x\right)\right)}^{2}dx$

C. $S=\mathrm{\pi }{\int }_a^b\left({f_1}^2\left(x\right)-{f_2}^2\left(x\right)\right)dx$

D. $S={\int }_a^b\left(f_1\left(x\right)-f_2\left(x\right)\right)dx$ 

Xem lời giải »

Câu 1:

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường $y=\sqrt{2-x}; y=x$ xung quanh trục Ox được tính theo công thức nào sau đây?

A. $V=\mathrm{\pi }{\int }_0^2\left(2-\mathrm{x}\right)\mathrm{dx}+\mathrm{\pi }{\int }_0^2{\mathrm{x}}^2\mathrm{dx}$

B. $V=\mathrm{\pi }{\int }_0^2\left(2-\mathrm{x}\right)\mathrm{dx}$

C. $V=\mathrm{\pi }{\int }_0^{1}xdx+\mathrm{\pi }{\int }_1^2\sqrt{2-\mathrm{x}}\mathrm{dx}$

D. $V={\int }_0^1{x}^2\mathrm{dx}+\mathrm{\pi }{\int }_1^2\left(2-\mathrm{x}\right)\mathrm{dx}$ 

Xem lời giải »

Câu 2:

Tính thể tích V của một vật tròn xoay tạo thành khi quay hình phẳng $y=x^2; y=\sqrt{x}$ (H) giới hạn bởi các đường  quanh trục Ox

A. $V=\frac{7\mathrm{\pi }}{10}$

B. $V=\frac{9\mathrm{\pi }}{10}$

C. $V=\frac{3\mathrm{\pi }}{10}$

D. $V=\frac{\mathrm{\pi }}{10}$ 

Xem lời giải »

Câu 3:

Trong mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường $4y=x^2$ và y = x. Thể tích của vật thể tròn xoay khi quay hình (H) quanh trục hoành một vòng bằng:

A. $\frac{128}{30}\mathrm{\pi }$

B. $\frac{128}{15}\mathrm{\pi }$

C. $\frac{32}{15}\mathrm{\pi }$

D. $\frac{129}{30}\mathrm{\pi }$ 

Xem lời giải »

Câu 4:

Cho vật thể V được giới hạn bởi hai mặt phẳng x=a và x=b (a<b), mặt phẳng vuông góc với trục Ox cắt V theo thiết diện S(x). Thể tích của V được tính bởi:

A. $V={\int }_a^{b}S\left(x\right)dx$

B. $V=\mathrm{\pi }{\int }_a^{b}S\left(x\right)dx$

C. $V={\int }_a^b{S}^2\left(x\right)dx$

D. $V=\mathrm{\pi }{\int }_a^b{S}^2\left(x\right)dx$ 

Xem lời giải »

Câu 5:

Cho vật thể V được giới hạn bởi hai mặt phẳng x = 0 và x = - 2, mặt phẳng vuông góc với trục Ox cắt V theo thiết diện $S\left(x\right)=2x^2$. Thể tích của V được tính bởi:

A. $V={\int }_{-2}^{0}4x^{4}dx$

B. $V={\int }_0^{-2}2x^{2}dx$

C. $V={\int }_{-2}^{0}2x^{2}dx$

D. $V=\mathrm{\pi }{\int }_{-2}^{0}4x^{4}dx$ 

Xem lời giải »

Câu 6:

Viết công thức tính thể tích V của phần vật thể nằm giữa hai mặt phẳng x = 0 và x = ln4, biết khi cắt vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x $\left(0\le x\le \ln 4\right)$, ta được thiết diện là một hình vuông có độ dài cạnh là: $\sqrt{x.e^x}$

A. $V={\int }_0^{\ln 4}x{e}^{x}dx$

B. $V=\mathrm{\pi }{\int }_0^{\ln 4}x{e}^{x}dx$

C. $V=\mathrm{\pi }{\int }_0^{\ln 4}{\left(x{e}^x\right)}^{2}dx$

D. $V={\int }_0^{\ln 4}\sqrt{x{e}^x}dx$ 

Xem lời giải »

Câu 7:

Cho hình phẳng (H) giới hạn bởi các đường $y=-x^2+2x$ và y = 0. Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Oy là:

A. $V=\frac{7}{3}\mathrm{\pi }$

B. $V=\frac{8}{3}\mathrm{\pi }$

C. $V=\frac{10}{3}\mathrm{\pi }$

D. $V=\frac{16}{3}\mathrm{\pi }$ 

Xem lời giải »

Câu 8:

Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi đường (E): $\frac{x^2}{16}+\frac{y^2}{9}=1$ quay quanh Oy?

A. $V=36\mathrm{\pi }$

B. $V=24\mathrm{\pi }$

C. $V=14\mathrm{\pi }$

D. $V=64\mathrm{\pi }$ 

Xem lời giải »

Câu 9:

Trong mặt phẳng tọa độ Oxy, gọi $\left(H_1\right)$ là hình phẳng giới hạn bởi các đường $y=\frac{x^2}{4}; y=-\frac{x^2}{4}; x=4; x=-4$ và $\left(H_2\right)$ là hình gồm tất cả các điểm (x;y) thỏa mãn $x^2+y^2\le 16, x^2+{\left(y-2\right)}^2\ge 4; x^2+{\left(y+2\right)}^2\ge 4$

Cho $\left(H_1\right)$ và $\left(H_2\right)$ quay quanh trục Oy ta được các vật thể có thể tích là $V_1, V_2$. Đẳng thức nào sau đây đúng?

A. $V_1=\frac{1}{2}{V}_2$

B. $V_1=V_2$

C. $V_1=\frac{2}{3}{V}_2$

D. $V_1=2V_2$ 

Xem lời giải »

Câu 10:

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị $y=-\sqrt{4-x^2}, x^2+3y=0$ quay quanh trục Ox là $V=\frac{a\mathrm{\pi }\sqrt{3}}{b}$ với a, b > 0 và $\frac{a}{b}$ là phân số tối giản. Tính tổng T = a + b

A. 33

B. 31

C. 29

D. 27

Xem lời giải »

Câu 11:

Gọi D là hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, cung tròn có phương trình $y=\sqrt{6-x^2}$ $\left(-\sqrt{6}\le x\le \sqrt{6}\right)$ và trục hoành (phần tô đậm trong hình vẽ). Tính thể tích V của vật thể tròn xoay sinh bởi khi quay hình phẳng D quanh trục Ox.

A. $V=8\mathrm{\pi }\sqrt{6}-2\mathrm{\pi }$

B. $V=8\mathrm{\pi }\sqrt{6}+\frac{22\mathrm{\pi }}{3}$

C. $V=8\mathrm{\pi }\sqrt{6}-\frac{22\mathrm{\pi }}{3}$

D. $V=4\mathrm{\pi }\sqrt{6}+\frac{22\mathrm{\pi }}{3}$