Top 50 bài tập Phương trình mũ và phương trình Lôgarit (mới nhất)

Câu 1:

Giả sử x là nghiệm của phương trình $4^{\frac{1}{x}-2}=\frac{\ln \sqrt{e}}{2}$. Tính lnx

A. 0

B. ln3

C. -ln3

D. 1

Xem lời giải »

Câu 2:

Tính tích tất cả các nghiệm của phương trình $3^{2x^2+2x+1}-28.3^{x^2+x}+9=0$

A. -4

B. -2

C. 2

D. 4

Xem lời giải »

Câu 3:

Tìm nghiệm của phương trình $2^{x-1}=3^{1-2x}$

A. $x=\frac{2{\log }_{2}3}{2{\log }_{2}3+1}$

B. $x=\frac{{\log }_{2}3+1}{{\log }_{2}3+2}$

C. $x=\frac{2{\log }_{2}3+1}{{\log }_{2}3+2}$

D. $x=\frac{{\log }_{2}3+1}{2{\log }_{2}3+1}$

Xem lời giải »

Câu 4:

Giải phương trình $(x^2-2x)lnx=ln{x}^3$

A. x = 1, x = 3    

B. x = -1, x = 3     

C. x = ±1, x = 3    

D. x = 3

Xem lời giải »

Câu 5:

Nếu ${\log }_7\left({\log }_3\right({\log }_{2}x\left)\right) = 0$ thì $x^{-\frac{1}{2}}$ bằng :

A. $\frac{1}{3}$

B. $\frac{1}{\sqrt{42}}$

C. $\frac{1}{2\sqrt{2}}$

D. $\frac{1}{3\sqrt{3}}$

Xem lời giải »

Câu 6:

Giải phương trình logx = log(x + 3) - log(x - 1)

A. x = 1   

B. x = 3   

C. x = 4    

D. x = -1, x = 3

Xem lời giải »

Câu 7:

Giải phương trình ${\log }_{\sqrt{2}}(x+1)=lo{g}_2(x^2+2)-1$

A. x = 1   

B. x = 0   

C. x = 0, x = -4   

D. x = 0, x = 1

Xem lời giải »

Câu 8:

Cho biết $lo{g}_{b^2}x+lo{g}_{x^2}b=1$, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng:

A. b

B. $\sqrt{b}$

C. $\frac{1}{b}$

D. $\frac{1}{b^2}$

Xem lời giải »

Câu 9:

Cho biết $2^x=8^{y+1} và 9^y=3^{x-9}.$ Tính giá trị của x + y?

A. 21

B. 18

C. 24

D. 27

Xem lời giải »

Câu 10:

Giả sử x, y là hai số thực thỏa mãn đồng thời $3^{x^2-2xy}=1$ và $2{\log }_{3}x = {\log }_3(y + 3)$. Tính x + y

A. 4

B. 2

C. 3

D. 9

Xem lời giải »

Câu 11:

Giải phương trình ${10}^x=0,00001$

A. x = -log4    

B. x = -log5    

C. x = -4    

D. x = -5

Xem lời giải »

Câu 12:

Giải phương trình $\frac{2}{1-e^{-2x}}=4.$

A. x=ln2

B. $x=\frac{1}{2}\ln 2$

C. $x=\frac{1}{4}\ln 2$

D. $x=-\ln \sqrt{2}$

Xem lời giải »

Câu 13:

Cho phương trình $5^{x-1}={\left(\frac{1}{25}\right)}^x$

Nghiệm của phương trình này nằm trong khoảng nào dưới đây?

A. $\left(0;\frac{1}{2}\right)$

B. $\left(-\frac{3}{2};-\frac{1}{2}\right)$

C. $\left(\frac{1}{2};1\right)$

D. $\left(-\frac{1}{2};0\right)$

Xem lời giải »

Câu 14:

Giải phương trình $3^{2x-3}=7$. Viết nghiệm dưới dạng thập phân, làm tròn đến hàng phần nghìn.

A. x ≈ 2,38   

B. x ≈ 2,386    

C. x ≈ 2,384   

D. x ≈ 1,782

Xem lời giải »

Câu 15:

Tính tổng bình phương các nghiệm của phương trình $4^{x^2+2}-9.2^{x^2+2}+8=0$

A. 2

B. 4

C. 17

D. 65

Xem lời giải »

Câu 16:

Giải phương trình $4^x+2^{x+1}-15=0.$ Viết nghiệm tìm được dưới dạng thập phân, làm tròn đến hàng phần trăm

A. x ≈ 0,43     

B. x ≈ 0,63    

C. x ≈ 1,58    

D. x ≈ 2,32

Xem lời giải »

Câu 17:

Giải phương trình $4^x+2^{x+1}-15=0.$ Viết nghiệm tìm được dưới dạng thập phân, làm tròn đến hàng phần trăm

A. x ≈ 0,43     

B. x ≈ 0,63    

C. x ≈ 1,58    

D. x ≈ 2,32

Xem lời giải »

Câu 18:

Tìm nghiệm của phương trình $4^{1-x}=3^{2x+1}$

A. $x=\frac{{\log }_{3}2-1}{2{\log }_{3}2+1}$

B. $x=\frac{{\log }_{3}2-1}{2\left({\log }_{3}2-1\right)}$

C. $x=\frac{2{\log }_{3}2-1}{2\left({\log }_{3}2+1\right)}$

D. $x=\frac{2{\log }_{3}2-1}{2{\log }_{3}2\times 1}$

Xem lời giải »

Câu 19:

Giải phương trình ${\log }_5(x + 4) = 3$

A. x = 11    

B. x = 121    

C. x = 239    

D. x = 129

Xem lời giải »

Câu 20:

Tìm các số thực a thỏa mãn $lo{g}_{10}(a^2-15a)=2$

A. 20 và -5

B. $\pm 20$

C. $\frac{15\pm \sqrt{233}}{2}$

D. $\frac{15\pm \sqrt{305}}{2}$

Xem lời giải »

Câu 21:

Giải phương trình $x^{2}lnx=ln{x}^9$

A. x = 3   

B. x = ±3    

C. x = 1, x = 3    

D. x = 1, x = ±3

Xem lời giải »

Câu 22:

Giải phương trình ${\log }_4\left({\log }_3\right({\log }_{2}x\left)\right) = 0$?

A. x = 2    

B. x = 8    

C. $x = \sqrt[3]{2}$

D. $x={4^3}^2$

Xem lời giải »

Câu 23:

Giải phương trình lnx + ln(x - 1) = ln2

A. x = 3/2    

B. x = -1, x = 2    

C. x = 2    

D. x = 1, x = 3/2

Xem lời giải »

Câu 24:

Giả sử α < β là hai nghiệm của phương trình $3 + 2{\log }_{2}x = {\log }_2(14x - 3)$. Khẳng định nào sau đây là đúng ?

A. α = -4    

B. ${\log }_2\alpha = -2$

C. $\alpha = \frac{3}{2}$

D. $\alpha = \frac{3}{14}$

Xem lời giải »

Câu 25:

Tính tích các nghiệm của phương trình ${\log }_{x}4 + {\log }_{4}x = \frac{17}{4}.$

A. 1

B. 16

C. $4\sqrt[4]{4}$

D. $256\sqrt{2}$

Xem lời giải »

Câu 26:

Tìm hai số x và y đồng thời thỏa mãn $3^{x+y}=81$ và ${81}^{x-y}=3$

A. $x=2\frac{1}{8}; y=1\frac{7}{8}$

B. $x=2\frac{1}{2}; y=1\frac{1}{2}$

C. $x=2\frac{1}{4}; y=1\frac{3}{4}$

D. $x=2; y=2$

Xem lời giải »

Câu 27:

Một quần thể vi khuẩn bắt đầu từ 100 cá thể và cứ sau 3 giờ thì số cá thể lại tăng gấp đôi. Bởi vậy, số cá thể vi khuẩn được biểu thị theo thời gian t (tính bằng giờ) bằng công thức $N\left(t\right)=100.2^{\frac{t}{3}}$. Hỏi sau bao lâu thì quần thể này đạt đến 50000 cá thể (làm tròn kết quả đến hàng phần mười)? 

A. 36,8 giờ   

B. 30,2 giờ    

C. 26,9 giờ   

D. 18,6 giờ

Xem lời giải »

Câu 28:

Khi đèn flash của một máy ảnh tắt thì ngay lập tức nguồn điện từ pin sẽ xạc cho tụ điện của nó. Lượng điện tích trong tụ xác định bởi công thức $Q\left(t\right)=Q_0\left(1-e^{-\frac{1}{t}}\right)$ trong đó $Q_0$ là điện tích tối đa mà tụ có thể tích được, thời gian t tính bằng giây. Hỏi sau bao lâu thì tụ tích được 90% điện tích tối đa ?

A. 3,2 giây   

B. 4,6 giây    

C. 4,8 giây    

D. 9,2 giây

Xem lời giải »

Câu 29:

Chiều dài (tính bằng xentimet) của một loài cá bơn ở Thái Bình Dương theo tuổi của nó (kí hiệu là t, tính bằng năm) được ước lượng bởi công thức $f\left(t\right) = 200(1 - 0,956e^{-0,18t}).$ Một con cá bơn thuộc loài này có chiều dài 140cm. Hãy ước lượng tuổi của nó.

A. 2,79 năm   

B. 6,44 năm    

C. 7,24 năm    

D. 12,54 năm

Xem lời giải »

Câu 30:

Có một dịch cúm trong một khu vực quân đội và số người lính ở đó mắc bệnh cúm sau t ngày (kể từ ngày dịch cúm bùng phát) được ước lượng bằng công thức $Q\left(t\right)=\frac{5000}{1+1249e^{-kt}}$ trong đó k là một hằng số. Biết rằng có 40 người lính mắc bệnh cúm sau 7 ngày. Tìm giá trị của hằng số k. 

A. 0,33   

B. 2,31    

C. 1,31    

D. -2,31

Xem lời giải »

Câu 31:

Nếu log(log(log(logx))) = 0 thì $x={10}^k.$ Tìm giá trị của k?

A. 10    

B. 100    

C. ${10}^3$    

D. ${10}^{10}$ 

Xem lời giải »

Câu 32:

Giải phương trình ${\log }_{3}x = (-2 + {\log }_{2}100)\left({\log }_3\sqrt{2}\right)$

A. x = 5    

B. $x = 3\sqrt{2}$

C. $x=2^4$   

D. x = 50

Xem lời giải »

Câu 33:

Tìm tập hợp các nghiệm của phương trình $x^{\log x}=\frac{x^3}{100}$

A. {10}

B. {10;100}

C. $\left\{\frac{1}{10};10\right\}$

D. $\left\{\frac{1}{10};100\right\}$

Xem lời giải »

Câu 1:

Phương trình $4^{2x+5}=2^{2-x}$ có nghiệm là:

A. $\frac{-8}{5}$

B. 3

C. $\frac{8}{5}$

D. $\frac{12}{5}$

Xem lời giải »

Câu 2:

Tổng các nghiệm của phương trình $3^{x^4-3x^3}=81$

A. 0

B. 1

C. 3

D. 4

Xem lời giải »

Câu 3:

Giải phương trình $4^x=8^{x-1}$

A. x=-3

B. x=-2

C. x=2

D. x=3

Xem lời giải »

Câu 4:

Số nghiệm của phương trình $2^{2x^2-7x+5}=1$ là:

A. 2

B. 1

C. 3

D. 0

Xem lời giải »

Câu 5:

Tìm tập hợp tất cả các nghiệm của phương trình $2^{x^2+x-1}=\frac{1}{2}$

A. $\left\{-1;2\right\}$

B. $\left\{0;1\right\}$

C. $\left\{-1;0\right\}$

D. $\left\{-2;1\right\}$

Xem lời giải »

Câu 6:

Tìm tập nghiệm S của phương trình $4^{x+1}+4^{x-1}=272$

A. S={1}

B. S={3}

C. S={2}

D. S={5}

Xem lời giải »

Câu 7:

Giá trị của x thỏa mãn ${\log }_{\frac{1}{2}}\left(3-x\right)=2$ là:

A. $x=3+\sqrt{2}$

B. $x=-\frac{11}{4}$

C. $x=3-\sqrt{2}$

D. $x=\frac{11}{4}$

Xem lời giải »

Câu 8:

Tính P là tích tất cả các nghiệm của phương trình ${\log }_{\frac{1}{2}}\frac{x^2-3x+2}{x}=0$

A. P=4

B. $P=2\sqrt{2}$

C. P=2

D. P=1

Xem lời giải »

Câu 9:

Tập nghiệm của phương trình ${\log }_2\left(x^2-1\right)={\log }_{2}2x$ là:

A. $\left\{\frac{1+\sqrt{2}}{2}\right\}$

B. $\left\{2;41\right\}$

C. $\{1-\sqrt{2};1+\sqrt{2}\}$

D. $\left\{1+\sqrt{2}\right\}$

Xem lời giải »

Câu 10:

Biết rằng phương trình $2\log (x+2)=\log 4=\log x+4\log 3$ có hai nghiệm phân biệt $x_1,x_2(x_1<x_2)$. Tính $P=\frac{x_1}{x_2}$

A. P=4

B. $P=\frac{1}{4}$

C. P=64

D. $P=\frac{1}{64}$

Xem lời giải »

Câu 11:

Giải phương trình ${\log }_3\left(2x-1\right)=2$, ta có nghiệm là:

A. x=15

B. $x=\frac{1}{5}$

C. x=25

D. x=5

Xem lời giải »

Câu 12:

Tập nghiệm của phương trình ${\log }_2\left(x^2-x+2\right)=1$

A. $\left\{0\right\}$

B. $\left\{0;1\right\}$

C. $\left\{-1;0\right\}$

D. $\left\{1\right\}$

Xem lời giải »

Câu 13:

Giải phương trình ${\log }_4\left(x-1\right)=3$

A. x=63

B. x=65

C. x=82

D. x=80

Xem lời giải »

Câu 14:

Tìm tập nghiệm S của phương trình ${\log }_2\left(x-1\right)+{\log }_2\left(x+1\right)=3$

A. $S=\left\{-3;3\right\}$

B. $S=\left\{\sqrt{10}\right\}$

C. $S=\left\{3\right\}$

D. $\left\{-\sqrt{10};\sqrt{10}\right\}$

Xem lời giải »

Câu 15:

Số nghiệm của phương trình ${\log }_4\left({\log }_{2}x\right)+{\log }_2\left({\log }_{4}x\right)=2$ là

A. 0

B. 1

C. 2

D. Nhiều hơn 2

Xem lời giải »

Câu 16:

Giải phương trình ${\log }_4\left(x+1\right)+{\log }_4(x-3)=3$

A. $x=1\pm 2\sqrt{17}$

B. $x=1+2\sqrt{17}$

C. x=33

D. x=5

Xem lời giải »

Câu 17:

Tổng lập phương các nghiệm của phương trình ${\log }_2.{\log }_3(2x-1)=2{\log }_{2}x$ bằng:

A. 6

B. 26

C. 126

D. 216

Xem lời giải »

Câu 18:

Tìm nghiệm của phương trình $9^{\sqrt{x-1}}=e^{\ln 81}$

A. x=5

B. x=4

C. x=6

D. x=17

Xem lời giải »

Câu 19:

Tìm nghiệm của phương trình $\frac{3^{2x-6}}{27}={\left(\frac{1}{3}\right)}^x$

A. x=4

B. x=2

C. x=5

D. x=3

Xem lời giải »

Câu 20:

Cho a là số thực dương, khác 1 và thỏa mãn $\frac{1}{2}\left(a^{\alpha }+a^{-\alpha }\right)=1$. Tìm $\alpha$

A. $\alpha =1$

B. $\alpha \in R$

C. $\alpha =0$

D. $\alpha =-1$

Xem lời giải »

Câu 1:

Giải phương trình $9^{\left|x+1\right|}={27}^{2x-2}$. Ta có tập nghiệm bằng:

A. $\left\{2\right\}$

B. $\left\{2;\frac{1}{2}\right\}$

C. $\left\{1\right\}$

D. $\left\{3;\frac{1}{4}\right\}$

Xem lời giải »

Câu 2:

Tính tổng T tất cả các nghiệm của phương trình $4.9^x-13.6^x+9.4^x=0$

A. T=2

B. T=3

C. $T=\frac{13}{4}$

D. $T=\frac{1}{4}$

Xem lời giải »

Câu 3:

Giải phương trình $\sqrt{3^x+6}=3^x$ có tập nghiệm bằng

A. $\left\{1;{\log }_{3}2\right\}$

B. $\left\{-2;3\right\}$

C. $\left\{1\right\}$

D. $\left\{3\right\}$

Xem lời giải »

Câu 4:

Khi đặt $3^x=t$ thì phương trình $9^{x+1}-3^{x+1}-30=0$ trở thành

A. $3t^2-t-10=0$

B. $9t^2-3t-10=0$

C. $t^2-t-10=0$

D. $2t^2-t-1=0$

Xem lời giải »

Câu 5:

Tìm tích các nghiệm của phương trình ${\left(\sqrt{2}-1\right)}^x+{\left(\sqrt{2}+1\right)}^x-2\sqrt{2}=0$

A. 2

B. -1

C. 0

D. 1

Xem lời giải »

Câu 6:

Cho số thực x thỏa mãn $2=5{\log }_{3}x$. Mệnh đề nào sau đây đúng?

A. $2=3^{{\log }_{5}x}$

B. $5=x^{{\log }_{2}3}$

C. $2=x^{{\log }_{3}5}$

D. $3=5^{\log x}$

Xem lời giải »

Câu 7:

Trong các phương trình sau đây, phương trình nào có nghiệm?

A. $x^{\frac{2}{3}}+5=0$

B. ${\left(3x\right)}^{\frac{1}{3}}+{(x-4)}^{\frac{2}{5}}=0$

C. $\sqrt{4x-8}+2=0$

D. $2x^{\frac{1}{2}}-3=0$

Xem lời giải »

Câu 8:

Tổng bình phương các nghiệm của phương trình $5^{3x-2}={\left(\frac{1}{5}\right)}^{-x^2}$ bằng:

A. 2

B. 5

C. 0

D. 3

Xem lời giải »

Câu 9:

Tìm tập nghiệm S của phương trình ${\log }_2\left(x^2-4x+3\right)={\log }_2\left(4x-4\right)$

A. $S=\left\{1;7\right\}$

B. $S=\left\{7\right\}$

C. $S=\left\{1\right\}$

D. $S=\left\{3;7\right\}$

Xem lời giải »

Câu 10:

Tính P tích tất cả các nghiệm của phương trình ${\log }_{2}x-{\log }_{x}64=1$

A. P=1

B. P=2

C. P=4

D. P=8

Xem lời giải »

Câu 11:

Phương trình ${\log }_{2017}x+{\log }_{2016}x=0$ có tất cả bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 3

Xem lời giải »

Câu 12:

Phương trình ${\log }_4\left(3.2^x-1\right)=x-1$ có hai nghiệm là $x_1;x_2$ thì tổng $x_1+x_2$ là:

A. ${\log }_2\left(6-4\sqrt{2}\right)$

B. 4

C. 2

D. $6+4\sqrt{2}$

Xem lời giải »

Câu 13:

Phương trình ${\log }_{\sqrt{3}}x+\frac{1}{{\log }_{3}x}=3$ có số nghiệm hữu tỉ là:

A. 2

B. 1

C. 0

D. 3

Xem lời giải »

Câu 14:

Giải phương trình ${\log }_3\left(x+2\right)+{\log }_9{\left(x+2\right)}^2=\frac{5}{4}$

A. x=1

B. $x=\sqrt[8]{3^5}-2$

C. $x=\sqrt[4]{3^5}-2$

D. $x=\sqrt[4]{3}-2$

Xem lời giải »

Câu 15:

Phương trình ${\log }_2\left(x-3\right)+2{\log }_{4}3.{\log }_{3}x=2$ có tất cả bao nhiêu nghiệm?

A. 1

B. 2

C. 3

D. 0

Xem lời giải »

Câu 16:

Số nghiệm thực phân biệt của phương trình $4^{x^2}-5.2^{x^2}+4=0$

A. 3

B. 2

C. 0

D. 1

Xem lời giải »

Câu 17:

Cho hai số thực dương a và b thỏa mãn ${\log }_{4}a={\log }_{6}b={\log }_9\left(a+b\right)$. Tính tỉ số $\frac{a}{b}$

A. $\frac{-1+\sqrt{5}}{2}$

B. $\frac{-1-\sqrt{5}}{2}$

C. $\frac{1+\sqrt{5}}{2}$

D. $\frac{1}{2}$

Xem lời giải »

Câu 18:

Tập hợp nghiệm của phương trình ${\log }_3\left(9^{50}+6x^2\right)={\log }_{\sqrt{3}}\left(3^{50}+2x\right)$ là:

A. $\left\{0;1\right\}$

B. $\left\{0;2.3^{50}\right\}$

C. $\left\{0\right\}$

D. R

Xem lời giải »

Câu 19:

Giải phương trình ${\log }_2\left(2^x-1\right).{\log }_4\left(2^{x+1}-2\right)=1$. Ta có nghiệm:

A. $x={\log }_{2}3$ và $x={\log }_{2}5$

B. x=1 và x=-2

C. $x={\log }_{2}3$ và ${\log }_2\frac{5}{4}$

D. x=1 và x=2

Xem lời giải »

Câu 20:

Cho a, b, x là các số thực dương khác 1 thỏa: $4{\log }_a^{2}x+3{\log }_b^{2}x=8{\log }_{a}x.{\log }_{b}x$ (1). Mệnh đề (1) tương đương với mệnh đề nào sau đây:

A. $a=b^2$

B. $a=b^2$ và $a^3=b^2$

C. $a^3=b^2$

D. $x=ab$

Xem lời giải »

Câu 1:

Biết rằng phương trình ${\log }_3\left(3^{x+1}-1\right)=2x+{\log }_{\frac{1}{3}}2$ có hai nghiệm $x_1$ và $x_2$. Hãy tính tổng $S={27}^{x_1}+{27}^{x_2}$

A. S=180

B. 45

C. S=9

D. S=252

Xem lời giải »

Câu 2:

Tìm m để phương trình $4^x-2^{x+3}+3=m$ có đúng 2 nghiệm $x\in \left(1;3\right)$

A. -13<m<-9

B. 3<m<9

C. -9<m<3

D. -13<m<3

Xem lời giải »

Câu 3:

Tìm giá trị của tham số m để phương trình $9^x-m.3^{x+2}+9m=0$ có hai nghiệm phân biệt $x_1;x_2$ thỏa mãn $x_1+x_2=3$

A. m=4

B. m=1

C. $m=\frac{5}{2}$

D. m=3

Xem lời giải »

Câu 4:

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt $9^{1-x}+2\left(m-1\right)3^{1-x}+1=0$

A. m>1

B. m<-1

C. m<0

D. -1<m<0

Xem lời giải »

Câu 5:

Biết phương trình $9^x-2^{x+\frac{1}{2}}=2^{x+\frac{3}{2}}-3^{2x-1}$ có nghiệm là a. Tính giá trị của biểu thức $P=a+\frac{1}{2}{\log }_{\frac{9}{2}}2$

A. $P=\frac{1}{2}$

B. $P=1-{\log }_{\frac{9}{2}}2$

C. P=1

D. $P=1-{\log }_{\frac{9}{2}}2$

Xem lời giải »

Câu 6:

Biết rằng phương trình $2^{x^2-1}=3^{x+1}$ có hai nghiệm là a và b. Khi đó a+b+ab có giá trị bằng

A. $-1+2{\log }_{2}3$

B. $1+{\log }_{2}3$

C. -1

D. $1+2{\log }_{2}3$

Xem lời giải »

Câu 7:

Biết rằng phương trình $3^{x^2+1}.{25}^{x-1}=\frac{3}{25}$ có đúng hai nghiệm $x_1;x_2$. Tính giá trị của $P=\sqrt{3^{x_1}+3^{x_2}}$

A. $P=\frac{\sqrt{26}}{5}$

B. $P=\sqrt{26}$

C. P=26

D. $P=\frac{26}{25}$

Xem lời giải »

Câu 8:

Tính tổng T tất cả các nghiệm của phương trình $5^{{\sin }^{2}x}+5^{{\cos }^{2}x}=2\sqrt{5}$ trên đoạn $\left[0;2\mathrm{\pi }\right]$

A. $T=\mathrm{\pi }$

B. $T=\frac{3\mathrm{\pi }}{4}$

C. $T=2\mathrm{\pi }$

D. $T=4\mathrm{\pi }$

Xem lời giải »

Câu 9:

Số nghiệm thực phân biệt của phương trình $2^{x+\frac{1}{4x}}+2^{\frac{x}{4}+\frac{1}{x}}=4$ là

A. 1

B. 2

C. 3

D. 0

Xem lời giải »

Câu 10:

Tìm giá trị m để phương trình $2^{\left|x-1\right|+1}+2^{\left|x-1\right|}+m=0$ có nghiệm duy nhất

A. m=3

B. $m=\frac{1}{8}$

C. m=-3

D. m=1

Xem lời giải »

Câu 11:

Tìm tất cả các giá trị thực của m để phương trình $2{\log }_2\left|x\right|+{\log }_2\left|x+3\right|=m$ có 3 nghiệm thực phân biệt:

A. $m\in \left(0;2\right)$

B. $m\in \left\{0;2\right\}$

C. $m\in \left(-\infty ;2\right)$

D. $m\in \left\{2\right\}$

Xem lời giải »

Câu 12:

Cho $x>0;x\ne 1$ thỏa mãn biểu thức $\frac{1}{{\log }_{2}x}+\frac{1}{{\log }_{3}x}+...+\frac{1}{{\log }_{2017x}}=M$. Khi đó x bằng:

A. $x=\sqrt[M]{2017!}-1$

B. $x=\sqrt[M]{2018!}$

C. $x=\sqrt[M]{2016!}$

D. $x=\sqrt[M]{2017!}$

Xem lời giải »

Câu 13:

Gọi $x_1,x_2$ là các nghiệm của phương trình ${\left({\log }_{\frac{1}{3}}x\right)}^2-\left(\sqrt{3}-1\right){\log }_{3}x+\sqrt{3}=0$. Khi đó tích $x_1.x_2$ bằng:

A. $3^{\sqrt{3}+1}$

B. $3^{-\sqrt{3}}$

C. 3

D. $3^{\sqrt{3}}$

Xem lời giải »

Câu 14:

Tìm tất cả các giá trị của tham số m để phương trình ${\log }_2^2+{\log }_{2}x+m=0$ có nghiệm $x\in \left(0;1\right)$

A. $m\ge \frac{1}{4}$

B. $m\le 1$

C. $m\le \frac{1}{4}$

D. $m\ge 1$

Xem lời giải »

Câu 15:

Tìm tất cả các giá trị thực của tham số m để phương trình ${\log }_3^{2}x-(m+2){\log }_{3}x+3m-1=0$ có hai nghiệm $x_1,x_2$ thỏa mãn $x_1.x_2=27$

A. m=-2

B. m=-1

C. m=1

D. m=2

Xem lời giải »

Câu 16:

Biết a, b là các số thực sao cho $x^3+y^3=a.{10}^{3x}+b.{10}^{2x}$, đồng thời x, y, z là các số thực dương thỏa mãn $\log \left(x+y\right)=z$ và $\log \left(x^2+y^2\right)=z+1$. Giá trị của $\frac{1}{a^2}+\frac{1}{b^2}$ thuộc khoảng:

A. (1;2)

B. (2;3)

C. (3;4)

D. (4;5)

Xem lời giải »

Câu 17:

Cho phương trình ${\log }_4\left(x^2-4x+4\right)+{\log }_{16}{\left(x+4\right)}^4-m=0$. Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.

A. $m<2{\log }_{2}3$

B. $m>-2{\log }_{2}3$

C. $m\in \varnothing$

D. $-2{\log }_{2}3<m<2{\log }_{2}3$

Xem lời giải »

Câu 18:

Tìm tập hợp tất cả các giá trị của tham số m để phương trình ${\log }_{2}x-{\log }_2\left(x-2\right)=m$ có nghiệm

A. $1\le m<+\infty$

B. $1<m<+\infty$

C. $0\le m<+\infty$

D. $0<m<+\infty$

Xem lời giải »

Câu 19:

Giá trị nguyên nhỏ nhất của tham số m để phương trình ${\log }_{3}x-{\log }_3\left(x-2\right)=m$ có nghiệm là

A. m=1

B. m=0

C. m=2

D. Không tồn tại

Xem lời giải »

Câu 20:

Tổng tất cả các nghiệm của phương trình ${\log }_3\left(7-3^x\right)=2-x$ bằng:

A. 2

B. 1

C. 7

D. 3

Xem lời giải »

Câu 1:

Tìm giá trị của a để phương trình ${\left(2+\sqrt{3}\right)}^x+\left(1-a\right){\left(2-\sqrt{3}\right)}^x$ $-4=0$ có 2 nghiệm phân biệt thỏa mãn: $x_1-x_2={\log }_{2+\sqrt{3}}3$, ta có a thuộc khoảng:

A. $\left(-\infty ;3\right)$

B. $\left(-3;+\infty \right)$

C. $\left(3;+\infty \right)$

D. $\left(0:+\infty \right)$

Xem lời giải »

Câu 2:

Tìm tập hợp tất cả các tham số m sao cho phương trình $4^{x^2-2x+1}-m.2^{x^2-2x+1}+3m-2=0$ có 4 nghiệm phân biệt.

A. $\left(-\infty ;1\right)$

B. $[2;+\infty )$

C. $\left(-\infty ;1\right)\cup \left(2;+\infty \right)$

D. $\left(2;+\infty \right)$

Xem lời giải »

Câu 3:

Có bao nhiêu số nguyên m thuộc $\left[-2020;2020\right]$ sao cho phương trình $4^{{\left(x-1\right)}^2}-4m.2^{x^2-2x}+3m-2=0$ có bốn nghiệm phân biệt?

A. 2020

B. 2018

C. 2016

D. 2020

Xem lời giải »

Câu 4:

Các giá trị thực của tham số m để phương trình: ${12}^x+\left(4-m\right).3^x-m=0$ có nghiệm thuộc khoảng (-1; 0) là

A. $m\in \left(\frac{17}{16};\frac{5}{2}\right)$

B. $m\in \left[2;4\right]$

C. $m\in \left(\frac{5}{2};6\right)$

D. $m\in \left(1;\frac{5}{2}\right)$

Xem lời giải »

Câu 5:

Tích các nghiệm của phương trình ${\left(3+\sqrt{5}\right)}^x+{\left(3-\sqrt{5}\right)}^x=3.2^x$ là:

A. 2

B. -2

C. 1

D. -1

Xem lời giải »

Câu 6:

Biết rằng tập hợp các giá trị của m để phương trình ${\left(\frac{1}{4}\right)}^{x^2}-\left(m+1\right).{\left(\frac{1}{2}\right)}^{x^2}-2m=0$ có nghiệm, là $\left[-a+2\sqrt{b};0\right]$ với a, b là các số nguyên dương. Tính b – a.

A. 1

B. -11

C. -1

D. 11

Xem lời giải »

Câu 7:

Tìm tập nghiệm S của phương trình $3^{x-1}.5^{\frac{2x-2-m}{x-m}}=15$, m là tham số khác 2.

A. $S=\left\{2;m{\log }_{3}5\right\}$

B. $S=\left\{2;m+{\log }_{3}5\right\}$

C. $S=\left\{2\right\}$

D. $S=\left\{2;m-{\log }_{3}5\right\}$

Xem lời giải »

Câu 8:

Tìm các giá trị m để phương trình $2^{x+!}=m.2^{x+2}-2^{x+3}$ luôn thỏa, $\forall x\in R$

A. $m=\frac{5}{2}$

B. $m=\frac{3}{2}$

C. m=3

D. m=2

Xem lời giải »

Câu 9:

Tính tổng T tất cả các nghiệm của phương trình ${\left(x-3\right)}^{2x^2-5x}=1$

A. $T=\frac{17}{2}$

B. $T=4$

C. $T=\frac{13}{2}$

D. $T=\frac{15}{2}$

Xem lời giải »

Câu 10:

Cho $4^x+4^{-x}=7$. Khi đó biểu thức $P=\frac{5-2^x-2^{-x}}{8+4.2^x+4.2^{-x}}=\frac{a}{b}$ với $\frac{a}{b}$ tối giản và $a,b\in Z$. Tích a.b có giá trị bằng:

A. 10

B. -8

C. 8

D. -10

Xem lời giải »

Câu 11:

Có bao nhiêu giá trị nguyên dương của tham số m để phương trình ${16}^x-2.{12}^x+\left(m-2\right).9^x=0$ có nghiệm dương?

A. 1

B. 2

C. 4

D. 3

Xem lời giải »

Câu 12:

Cho hàm số y=f(x) có bảng biến thiên như sau:

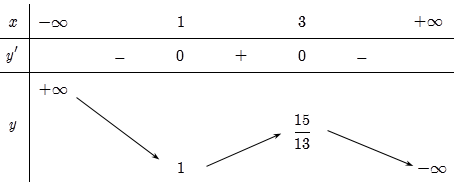
Biết $f\left(0\right)=\frac{7}{6}$, giá trị lớn nhất của m để phương trình $e^{3f^3\left(x\right)-\frac{13}{2}{f}^2\left(x\right)+7f\left(x\right)+\frac{3}{2}}=m$ có nghiệm trên đoạn [0;2] là:

A. $e^4$

B. $e^3$

C. $e^{\frac{15}{13}}$

D. $e^5$

Xem lời giải »

Câu 13:

Phương trình $2^{23x^3}.2^x-{1024}^{x^2}+23x^3=10x^2-x$ có tổng các nghiệm gần nhất với số nào dưới đây

A. 0,50

B. 0,35

C. 0,40

D. 0,45

Xem lời giải »

Câu 14:

Phương trình $2^{{\log }_5\left(x+3\right)}=x$ có tất cả bao nhiêu nghiệm?

A. 1

B. 2

C. 3

D. 0

Xem lời giải »

Câu 15:

Tìm m để phương trình $4^{\sqrt{x+1}+\sqrt{3-x}}-14.2^{\sqrt{x+1}+\sqrt{3-x}}+8=m$ có nghiệm

A. $-4\le m\le 3$

B. $-21\le m\le 33$

C. $-41\le m\le -32$

D. $m\ge 4$

Xem lời giải »

Câu 16:

Tính S là tổng tất cả các nghiệm của phương trình $4.2^{2x}-4.2^x+4.2^{-2x}-4.2^{-x}-7=0$

A. S=1

B. S=-1

C. S=3

D. S=0

Xem lời giải »

Câu 17:

Phương trình $x\left(2^{x-1}+4\right)=2^{x+1}+x^2$ có tổng các nghiệm bằng:

A. 7

B. 3

C. 5

D. 6

Xem lời giải »

Câu 18:

Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất $$\begin{gathered} 1+\left[2x^2-m\left(m+1\right)x-2\right].2^{1+mx-x^2} \\ =\left(x^2-mx-1\right).2^{mx\left(1-m\right)}+x^2-m^{2}x \end{gathered}$$

A. 0

B. 2

C. $-\frac{1}{2}$

D. $\frac{1}{2}$

Xem lời giải »

Câu 19:

Cho các số thực không âm x, y, z thỏa mãn $5^x+{25}^y+{125}^z=2020$. Giá trị nhỏ nhất của biểu thức $T=\frac{x}{6}+\frac{y}{3}+\frac{z}{2}$ là:

A. $\frac{1}{3}{\log }_{5}2020$

B. $\frac{1}{6}{\log }_{5}2018$

C. $\frac{1}{6}{\log }_{5}2020$

D. $\frac{1}{2}{\log }_{5}2018$

Xem lời giải »

Câu 20:

Cho phương trình ${\log }_{3}x.{\log }_{5}x={\log }_{3}x+{\log }_{5}x$. Khẳng định nào sau đây là đúng?

A. Phương trình có một nghiệm hữu tỉ và một nghiệm vô tỉ

B. Phương trình có một nghiệm duy nhất

C. Phương trình vô nghiệm

D.  Tổng các nghiệm của phương trình là một số chính phương

Xem lời giải »

Câu 21:

Phương trình ${\left(2+\sqrt{2}\right)}^{{\log }_{2}x}+x{\left(2-\sqrt{2}\right)}^{{\log }_{2}x}$ $=x^2+1$ có nghiệm là:

A. $x=\frac{1}{2}$

B. x=1

C. x=2

D. x=4

Xem lời giải »

Câu 22:

Tìm tập nghiệm của phương trình ${\log }_{3}x+\frac{1}{{\log }_{9}x}=3$

A. $\left\{1;2\right\}$

B. $\left\{\frac{1}{3};9\right\}$

C. $\left\{\frac{1}{3};3\right\}$

D. $\left\{3;9\right\}$

Xem lời giải »

Câu 23:

Cho phương trình $2{\log }_4\left(2x^2-x+2m-4m^2\right)$ $+{\log }_{\frac{1}{2}}\left(x^2+mx-2m^2\right)=0$. Tìm tất cả các giá trị của tham số m sao cho phương trình đã cho có hai nghiệm phân biệt $x_1,x_2$ thỏa mãn $x_1^2+x_2^2>1$

A. $[\begin{array}{c}-1<m<\frac{1}{3}\\ \frac{2}{5}<m<\frac{1}{2}\end{array}$

B. $[\begin{array}{c}-1<m<0\\ \frac{2}{5}<m<\frac{1}{2}\end{array}$

C. $[\begin{array}{c}-1\le m<0\\ \frac{1}{3}<m\le \frac{2}{5}\end{array}$

D. $[\begin{array}{c}m<0\\ m>\frac{2}{5}\end{array}$

Xem lời giải »

Câu 24:

Tính tổng tất cả các nghiệm thực của phương trình ${\log }_{\sqrt{3}}\left(x-2\right)+{\log }_3{(x-4)}^2=0$

A. $6+\sqrt{2}$

B. 6

C. $3+\sqrt{2}$

D. 9

Xem lời giải »

Câu 25:

Cho $0\le x\le 2020$ và ${\log }_2\left(2x+2\right)+x-3y=8^y$. Có bao nhiêu cặp số (x,y) nguyên thỏa mãn các điều kiện trên?

A. 2019

B. 2018

C. 1

D. 4

Xem lời giải »

Câu 26:

Phương trình sau đây có bao nhiêu nghiệm $(x^2-4)({\log }_{2}4+{\log }_{3}x+$ ${\log }_{4}x+...+{\log }_{19}x+{\log }_{20}^{2}x=0$

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 27:

Cho hàm số $f\left(x\right)={\log }_2\left(cosx\right)$. Phương trình f'(x)=0 có bao nhiêu nghiệm trong khoảng $\left(0;2020\mathrm{\pi }\right)$

A. 2020

B. 1009

C. 2010

D. 2019

Xem lời giải »

Câu 28:

Có bao nhiêu số nguyên $a\in \left(-2019;2019\right)$ để phương trình $\frac{1}{\ln \left(x+5\right)}+\frac{1}{3^x-1}=x+a$ có hai nghiệm phân biệt?

A. 0

B. 2022

C. 2014

D. 2015

Xem lời giải »

Câu 29:

Cho phương trình $m\ln \left(x+1\right)-x-2=0$. Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm $x_1,x_2$ thỏa mãn $0<x_1<2<4<x_2$ là khoảng $\left(a;+\infty \right)$A. Khi đó a thuộc khoảng nào dưới đây?

A. (3,7;3,8)

B. (3,6;3,7)

C. (3,8;3,9)

D. (3,5;3,6)

Xem lời giải »

Câu 30:

Cho phương trình  ${\log }_2\left(x-\sqrt{x^2-1}\right).{\log }_5\left(x-\sqrt{x^2-1}\right)$ $={\log }_m\left(x+\sqrt{x^2-1}\right)$. Có bao nhiêu giá trị nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2?

A. Vô số

B. 3

C. 2

D. 1

Xem lời giải »

Câu 31:

Hỏi phương trình $2{\log }_3\left(cotx\right)={\log }_2\left(\cos x\right)$ có bao nhiêu nghiệm trong khoảng $\left(0;2017\mathrm{\pi }\right)$

A. 1009

B. 1008

C. 2017

D. 2018

Xem lời giải »

Câu 32:

Có bao nhiêu số nguyên m để phương trình ${\log }_2\frac{3x^2+3x+m+1}{2x^2-x+1}=x^2-5x+2-m$ có hai nghiệm phân biệt lớn hơn 1.

A. 3

B. Vô số

C. 2

D. 4

Xem lời giải »

Câu 33:

Hỏi có bao nhiêu giá trị m nguyên trong đoạn $\left[-2017;2017\right]$ để phương trình $\log mx=2\log \left(x+1\right)$ có nghiệm duy nhất?

A. 2017

B. 4014

C. 2018

D. 4015

Xem lời giải »

Câu 34:

Biết rằng phương trình ${\left[{\log }_{\frac{1}{3}}\left(9x\right)\right]}^2+{\log }_3\frac{x^2}{81}-7=0$ có hai nghiệm phân biệt $x_1,x_2$. Tính $x_1.x_2$

A. $P=\frac{1}{9^3}$

B. $3^6$

C. $9^3$

D. $3^8$

Xem lời giải »

Câu 35:

Tìm m để phương trình $m\ln (1-x)-\ln x=m$ có nghiệm $x\in \left(0;1\right)$

A. $m\in \left(0;+\infty \right)$

B. $m\in \left(1;e\right)$

C. $m\in \left(-\infty ;0\right)$

D. $m\in \left(-\infty ;-1\right)$

Xem lời giải »

Câu 36:

Cho tham số thực a. Biết phương trình $e^x-e^{-x}=2\cos ax$ có 5 nghiệm thực phân biệt. Hỏi phương trình $e^x-e^{-x}=2\cos ax+4$ có bao nhiêu nghiệm thực phân biệt

A. 5

B. 6

C. 10

D. 11

Xem lời giải »

Câu 37:

Giả sử m là số thực sao cho phương trình ${\log }_3^{2}x-\left(m+2\right){\log }_{3}x+3m-2=0$ có hai nghiệm $x_1,x_2$ phân biệt thỏa mãn $x_1.x_2=9$.

Khi đó m thỏa mãn tính chất nào sau đây?

A. $m\in \left(3;4\right)$

B. $m\in \left(4;6\right)$

C. $m\in \left(-1;1\right)$

D. $m\in \left(1;3\right)$

Xem lời giải »

Câu 38:

Cho phương trình ${\log }_2^{2}x-\left(5m+1\right){\log }_{2}x+4m^2+m=0$. Biết phương trình có 2 nghiệm phân biệt $x_1,x_2$ thỏa mãn $x_1+x_2=165$. Giá trị của $\left|x_1-x_2\right|$ bằng:

A. 16

B. 119

C. 120

D. 159

Xem lời giải »

Câu 39:

Cho phương trình $m{\ln }^2(x+1)$ $-(x+2-m)\ln (x+1)-x-2=0 \left(1\right)$. Tập tất cả các giá trị của tham số m để phương trình (1) có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn $0<x_1<2<4<x_2$ là khoảng $\left(a;+\infty \right)$. Khi đó, a thuộc khoảng

A. (3,8;3,9)

B. (3,7;3,8)

C. (3,6;3,7)

D. (3,5;3,6) 

Xem lời giải »

Câu 40:

Cho x, y là các số thực dương thỏa mãn ${\log }_2\frac{3x+3y+4}{x^2+y^2}$ $=(x+y-1)(2x+2y-1)-4(xy-1)$. Giá trị lớn nhất của biểu thức $P=\frac{5x+3y-2}{2x+y+1}$ bằng:

A. 3

B. 1

C. 2

D. 4

Xem lời giải »

Câu 41:

Số nghiệm của phương trình ${\log }_3\left|x^2-\sqrt{2}x\right|={\log }_5\left(x^2-\sqrt{2}x+2\right)$

A. 3

B. 2

C. 1

D. 4

Xem lời giải »

Câu 42:

Phương trình ${\log }_3\frac{x^2-2x+1}{x}+x^2+1=3x$ có tổng tất cả các nghiệm bằng:

A. 3

B. 5

C. $\sqrt{5}$

D. 2

Xem lời giải »

Câu 43:

Cho a, b, c là các số thực dương khác 1 thỏa mãn ${\log }_a^{2}b+{\log }_b^{2}c={\log }_a\frac{c}{b}-2{\log }_b\frac{c}{b}-3$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P={\log }_{a}b-{\log }_{b}c$. Giá trị của biểu thức S=m-3M bằng:

A. S=-16

B. S=4

C. S=-6

D. S=6

Xem lời giải »

Câu 44:

Cho các số thực a, b, c thuộc khoảng $\left(1;+\infty \right)$ và thỏa mãn ${\log }_{\sqrt{a}}^{2}b+{\log }_{b}c.{\log }_b\left(\frac{c^2}{b}\right)$ $+9{\log }_{a}c=4{\log }_{a}b$. Giá trị của biểu thức ${\log }_{a}b+{\log }_b{c}^2$ bằng:

A. 1

B. $\frac{1}{2}$

C. 2

D. 3

Xem lời giải »

Câu 45:

Cho phương trình $4^{-\left|x-m\right|}.{\log }_{\sqrt{2}}\left(x^2-2x+3\right)$ $+2^{2x-x^2}.{\log }_{\frac{1}{2}}\left(2\left|x-m\right|+2\right)=0$ với m là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là:

A. 4

B. 1

C. 2

D. 3

Xem lời giải »

Câu 46:

Cho các số thực dương a, b, c khác 1 thỏa mãn  ${\log }_a^{2}b+{\log }_b^{2}c+2{\log }_b\frac{c}{b}={\log }_a\frac{c}{a^{3}b}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P={\log }_{a}ab-{\log }_{b}bc$. Tính giá trị của biểu thức $S=2m^2+9M^2$

A. S=28

B. S=25

C. S=26

D. S=27

Xem lời giải »