Top 50 bài tập Cộng, trừ và nhân số phức (mới nhất)

Câu 1:

Cho hai số phức $z_1 = 2 + 3i, z_2 = 1 - 2i .$ Tìm khẳng định sai

A. $z_1 + z_2 = 3 + i$

B. $z_1 - z_2 = 1+5i$

C. $z_1 . z_2 = 8 - i$

D. $z_1 . z_2 = 8 + i$

Xem lời giải »

Câu 2:

Cho hai số phức $z_1= - 3 + 4i, z_2 = 4 - 3i .$ Môđun của số phức $z = z_1 + z_2 + z_1. z_2$ là

A. 27

B. $\sqrt{27}$

C. $\sqrt{677}$

D. 677

Xem lời giải »

Câu 3:

Tìm các số thực x, y sao cho: (1 - 2i)x + (1 + 2i)y = 1 + i

A. $x=\frac{1}{4},y=\frac{3}{4}$

B. $x=\frac{1}{4},y=-\frac{3}{4}$

C. $x=-\frac{1}{4},y=\frac{3}{4}$

D. $x=-\frac{1}{4},y=-\frac{3}{4}$

Xem lời giải »

Câu 4:

Phần thực và phần ảo của số phức z = (3 + 4i)(4 - 3i) + (2 - i)(3 + 2i) là

A. 32 và 8i   

B. 32 và 8    

C. 18 và -14   

D. 32 và -8

Xem lời giải »

Câu 5:

Cho các số phức $z_1 = -1 + i, z_2 = 1 - 2i, z_3 = 1 + 2i .$ Giá trị của biểu thức $T = |z_1{z}_2 + z_2{z}_3 + z_3{z}_1|$ là

A. 1

B. $\sqrt{13}$

C. 5

D. 13

Xem lời giải »

Câu 6:

Tổng của hai số phức $z_1 = 1 - 2i, z_2 = 1 - 3i$ là

A. 2 + 5i   

B. 2 – 5i    

C. 1 + 5i   

D. 1 – 5i

Xem lời giải »

Câu 7:

Cho hai số phức $z_1 = 2 + 3i, z_2 = 2 - 4i .$ Hiệu $z_1 - z_2$ bằng

A. 2 + 7i   

B. 2 – i   

C. 7i   

D. – 7i

Xem lời giải »

Câu 8:

Tích của hai số phức $z_1 = 3 + 2i, z_2 = 2 - 3i$ là

A. 6 – 6i    

B. 12   

C. – 5i    

D. 12 – 5i

Xem lời giải »

Câu 9:

Số phức $z=(1+i{)}^2$ bằng

A. 2i

B. 1 + 3i    

C. – 2i    

D. 0

Xem lời giải »

Câu 10:

Số phức $z=(1-i{)}^3$ bằng

A. 1 + i   

B. – 2 – 2i    

C. – 2 + 2i    

D. 4 + 4i

Xem lời giải »

Câu 11:

Môđun của tổng hai số phức $z_1 = 3 - 4i$ và $z_2 = 4 + 3i$ là

A. $5\sqrt{2}$

B. 8

C. 10

D. 50

Xem lời giải »

Câu 12:

Cho z = -1 + 3i . Số phức $w = i\overline{z} + 2z$ bằng

A. 1 + 5i   

B. 1 + 7i   

C. – 1 + 5i    

D. – 1 + 7i

Xem lời giải »

Câu 13:

Cho z = 1 + 2i . Phần thực và phần ảo của số phức $w = 2z + \overline{z}$ là

A. 3 và 2    

B. 3 và 2i   

C. 1 và 6    

D. 1 và 6i

Xem lời giải »

Câu 14:

Cho số phức z thỏa mãn $(1 + 2i)z + \overline{z} = 2i .$ Khi đó tích $z.\overline{z}$ bằng

A. -2

B. 2

C. -2i

D. 2i

Xem lời giải »

Câu 15:

Môđun của số phức z thỏa mãn $2z + 3(1 - i)\overline{z} = 1 - 9i$ là

A. 5

B. 13

C. $\sqrt{5}$

D. $\sqrt{13}$

Xem lời giải »

Câu 16:

Cho hai số phức $z_1, z_2$ thỏa mãn $\left|z_1\right| = \left|z_2\right| = |z_1 + z_2| = 1 .$ Khi đó $|z_1 - z_2$| bằng

A. 0

B. 1

C. 2

D. $\sqrt{3}$

Xem lời giải »

Câu 17:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 1 - 2i| = 2 là

A. Đường tròn tâm I(1; -2) bán kính R = 2

B. Đường tròn tâm I(1; -2) bán kính R = 4

C. Đường tròn tâm I(-1; 2) bán kính R = 2

D. Đường tròn tâm I(-1; 2) bán kính R = 4

Xem lời giải »

Câu 1:

Cho hai số phức z = a + bi; z’ = a’ + b’i. Chọn công thức đúng:

A. $\mathrm{z}+\mathrm{z}\text{'}=$$\left(\mathrm{a}+\mathrm{b}\right)+\left(\mathrm{a}\text{'}+\mathrm{b}\text{'}\right)\mathrm{i}$

B. $\mathrm{z}-\mathrm{z}\text{'}=$$\left(\mathrm{a}+\mathrm{b}\right)-\left(\mathrm{a}\text{'}+\mathrm{b}\text{'}\right)\mathrm{i}$

C. $\mathrm{zz}\text{'}=$$\left(\mathrm{aa}\text{'}-\mathrm{bb}\text{'}\right)+\left(\mathrm{ab}\text{'}+\mathrm{a}\text{'}\mathrm{b}\right)\mathrm{i}$

D. $\mathrm{zz}\text{'}=$$\left(\mathrm{aa}\text{'}+\mathrm{bb}\text{'}\right)-\left(\mathrm{ab}\text{'}+\mathrm{a}\text{'}\mathrm{b}\right)\mathrm{i}$

Xem lời giải »

Câu 2:

Cho hai số phức ${\mathrm{z}}_1=1+2\mathrm{i}$ và ${\mathrm{z}}_2=2-3\mathrm{i}$. Xác định phần ảo a của số phức $\mathrm{z}=3{\mathrm{z}}_1-2{\mathrm{z}}_2$

A. a = 11

B. a = 12

C. a = -1

D. a = -12

Xem lời giải »

Câu 3:

Tìm số phức $\mathrm{w}={\mathrm{z}}_1-2{\mathrm{z}}_2$, biết rằng ${\mathrm{z}}_1=1+2\mathrm{i}$ và ${\mathrm{z}}_2=2-3\mathrm{i}$

A. $\mathrm{w}=-3-4\mathrm{i}$

B. $\mathrm{w}=-3+8\mathrm{i}$

C. $\mathrm{w}=3-\mathrm{i}$

D. $\mathrm{w}=5+8\mathrm{i}$

Xem lời giải »

Câu 4:

Cho hai số phức ${\mathrm{z}}_1=5-7\mathrm{i}$ và ${\mathrm{z}}_2=2+3\mathrm{i}$. Tìm số phức $\mathrm{z}={\mathrm{z}}_1+{\mathrm{z}}_2$

A. $\mathrm{z}=7-4\mathrm{i}$

B. $\mathrm{z}=2+5\mathrm{i}$

C. $\mathrm{z}=-2+5\mathrm{i}$

D. $\mathrm{z}=3-10\mathrm{i}$

Xem lời giải »

Câu 5:

Điểm nào trong hình vẽ dưới đây là biểu diễn hình học của số phức $\mathrm{z}=\left(-1-2\mathrm{i}\right)\left(3+\mathrm{i}\right)-2+6\mathrm{i}$

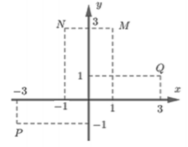
A. P

B. M

C. N

D. Q

Xem lời giải »

Câu 6:

Cho số phức z = a + bi và $\overline{\mathrm{z}}$ là số phức liên hợp của z. Chọn kết luận đúng:

A. $\mathrm{z}+\overline{\mathrm{z}}=2\mathrm{a}$

B. $\mathrm{z}.\overline{\mathrm{z}}=1$

C. $\mathrm{z}-\overline{\mathrm{z}}=2\mathrm{b}$

D. $\mathrm{z}.\overline{\mathrm{z}}={\mathrm{z}}^2$

Xem lời giải »

Câu 7:

Cho hai số phức ${\mathrm{z}}_1=3+4\mathrm{i},$${\mathrm{z}}_2=4-3\mathrm{i}$. Mệnh đề nào sau đây là đúng?

A. ${\mathrm{z}}_1=\overline{{\mathrm{z}}_2}$

B. ${\mathrm{z}}_1=-\overline{{\mathrm{z}}_2}$

C. ${\mathrm{z}}_1=-\mathrm{i}.{\mathrm{z}}_2$

D. ${\mathrm{z}}_1=\mathrm{i}.{\mathrm{z}}_2$

Xem lời giải »

Câu 8:

Cho hai số phức ${\mathrm{z}}_1=1+\mathrm{i}$ và ${\mathrm{z}}_2=2-3\mathrm{i}$. Tính mô đun của số phức ${\mathrm{z}}_1+{\mathrm{z}}_2$

A. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=\sqrt{13}$

B. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=\sqrt{5}$x

C. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=1$

D. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=5$

Xem lời giải »

Câu 9:

Cho hai số phức ${\mathrm{z}}_1=1+5\mathrm{i}$ và ${\mathrm{z}}_2=2+3\mathrm{i}$. Phần ảo của số phức $\mathrm{w}=3{\mathrm{z}}_1-{\mathrm{z}}_2$ là:

A. 18

B. 12i

C. 12

D. -1

Xem lời giải »

Câu 10:

Cho hai số phức ${\mathrm{z}}_1=2-3\mathrm{i}$ và ${\mathrm{z}}_2=-3+6\mathrm{i}$. Khi đó số phức ${\mathrm{z}}_1+{\mathrm{z}}_2$ bằng:

A. 1 - 9i

B. -1 - 9i

C. 1 + 3i

D. -1 + 3i

Xem lời giải »

Câu 11:

Cho hai số phức ${\mathrm{z}}_1=1+2\mathrm{i}$ và ${\mathrm{z}}_2=3-4\mathrm{i}$. Số phức $2{\mathrm{z}}_1+3{\mathrm{z}}_2$ là số phức nào sau đây?

A. 10 -10i

B. 8i

C. 11 -8i

D. 11 -8i

Xem lời giải »

Câu 12:

Cho các số phức z = 2 + i và w = 3 - 2i. Số phức w - z là:

A. 5 - i

B. -1 + 3i

C. 1 - 3i

D. 5 - 3i

Xem lời giải »

Câu 13:

Cho hai số phức ${\mathrm{z}}_1=1+\mathrm{i}$ và ${\mathrm{z}}_2=2-3\mathrm{i}$. Tính mô đun của số phức ${\mathrm{z}}_1-{\mathrm{z}}_2$

A. $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\sqrt{17}$

B. $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\sqrt{15}$

C. $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\sqrt{2}+\sqrt{13}$

D. $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=\sqrt{13}-\sqrt{2}$

Xem lời giải »

Câu 14:

Cho hai số phức ${\mathrm{z}}_1=2+3\mathrm{i}$ và ${\mathrm{z}}_2=3-2\mathrm{i}$. Tọa độ điểm biểu diễn số phức $z_1-z_2$ là:

A. (-1;5)

B. (-1;1)

C. (5;1)

D. (1;5)

Xem lời giải »

Câu 15:

Với hai số phức bất kì ${\mathrm{z}}_1,{\mathrm{z}}_2$. Khẳng định nào sau đây đúng:

A. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|\le \left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|$

B. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=\left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|$

C. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|\ge \left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|$

D. $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=\left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|+\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|$

Xem lời giải »

Câu 1:

Cho hai số phức ${\mathrm{z}}_1=2019+2020\mathrm{i}$ và ${\mathrm{z}}_2=2002\mathrm{i}$. Phần ảo của số phức ${\mathrm{iz}}_1-\overline{{\mathrm{z}}_2}$ bằng:

A. 2020

B. -4021

C. -2020

D. 4021

Xem lời giải »

Câu 2:

Tìm các giá trị của tham số thực x, y để số phức z = ${\left(\mathrm{x}+\mathrm{iy}\right)}^2-2\left(\mathrm{x}+\mathrm{iy}\right)+5$ là số thực.

A. x = 1 và y = 0

B. x = -1

C. x = 1 hoặc y = 0

D. x = 1

Xem lời giải »

Câu 3:

Cho số phức ${\mathrm{z}}_1=1+\mathrm{i},{\mathrm{z}}_2=2-3\mathrm{i}$. Phần ảo của số phức $\mathrm{w}={\mathrm{z}}_1+{\mathrm{z}}_2$ là:

A. -2

B. -3

C. 2

D. 3

Xem lời giải »

Câu 4:

Cho 2 số phức ${\mathrm{z}}_1=1+3\mathrm{i},\overline{{\mathrm{z}}_2}=4+2\mathrm{i}$. Tính mô đun của số phức ${\mathrm{z}}_2-2{\mathrm{z}}_1$

A. $2\sqrt{17}$

B. $2\sqrt{13}$

C. 4

D. $\sqrt{5}$

Xem lời giải »

Câu 5:

Cho số phức z = 2 + 3i. Tìm số phức $\mathrm{w}=\left(3+2\mathrm{i}\right)\mathrm{z}+2\overline{\mathrm{z}}$

A. w = 16 + 7i

B. w = 4 + 7i

C. w = 7 + 5i

D. w = 7 + 4i

Xem lời giải »

Câu 6:

Các số thực x, y thỏa mãn $\left(2-3\mathrm{i}\right)\mathrm{x}+\left(2+3\mathrm{y}\right)\mathrm{i}=2+2\mathrm{i}$ là:

A. x = 1; y = -1

B. x = 1; y = 1

C. x = -1; y = 1

D. x = -1; y = -1

Xem lời giải »

Câu 7:

Cho hai số phức ${\mathrm{z}}_1,{\mathrm{z}}_2$ thỏa mãn ${\mathrm{z}}_1.\overline{{\mathrm{z}}_1}=4,\left|{\mathrm{z}}_2\right|=3$. Giá trị biểu thức $\mathrm{P}={\left|{\mathrm{z}}_1\right|}^2+{\left|{\mathrm{z}}_2\right|}^2$ bằng:

A. 13

B. 25

C. 7

D. 19

Xem lời giải »

Câu 8:

Cho số phức $\mathrm{z}=\mathrm{a}+\mathrm{bi}\left(\mathrm{a},\mathrm{b}\in \mathrm{R}\right)$ thỏa mãn $\mathrm{z}-2\overline{\mathrm{z}}=-1+6\mathrm{i}$. Giá trị a + b bằng:

A. -1

B. -3

C. 2

D. 3

Xem lời giải »

Câu 9:

Với số phức z tùy ý, cho mệnh đề $\left|-\mathrm{z}\right|=\left|\mathrm{z}\right|;\left|\overline{\mathrm{z}}\right|=\left|\mathrm{z}\right|;$$\left|\mathrm{z}+\overline{\mathrm{z}}\right|=0,\left|\mathrm{z}\right|>0$. Số mệnh đề đúng là:

A. 2

B. 4

C. 1

D. 3

Xem lời giải »

Câu 10:

Cho số phức z = 2 + 5i. Tìm số phức $\mathrm{w}=\mathrm{iz}+\overline{\mathrm{z}}$

A. w = 7 - 3i

B. w = -3 - 3i

C. w = 3 + 7i

D. w = -7 - 7i

Xem lời giải »

Câu 11:

Cho số phức z thỏa mãn $\mathrm{z}+2\overline{\mathrm{z}}=6+2\mathrm{i}$. Điểm biểu diễn số phức z có tọa độ là:

A. (2;-2)

B. $\left(-2;-2\right)$

C. $\left(2;2\right)$

D. $\left(-2;2\right)$

Xem lời giải »

Câu 12:

Cho số phức z thỏa mãn $\left(1-\mathrm{i}\right)\mathrm{z}+2\mathrm{i}\overline{\mathrm{z}}=5+3\mathrm{i}$. Tìm số phức $\mathrm{w}=\mathrm{z}+2\overline{\mathrm{z}}$

A. w = 6 - i

B. w = -6 - i

C. w = 6 + i

D. w = -6 + i

Xem lời giải »

Câu 13:

Cho số phức $\mathrm{z}={\left(2\mathrm{i}-1\right)}^2-{\left(3+\mathrm{i}\right)}^2$. Tổng phần thực và phần ảo của z là:

A. 1

B. -1

C. -21

D. 21

Xem lời giải »

Câu 14:

Mô đun của số phức $\mathrm{z}=\left(2-3\mathrm{i}\right){\left(1+\mathrm{i}\right)}^4$ là:

A. $\left|\mathrm{z}\right|=4\sqrt{13}$

B. $\left|\mathrm{z}\right|=\sqrt{31}$

C. $\left|\mathrm{z}\right|=208$

D. $\left|\mathrm{z}\right|=\sqrt{13}$

Xem lời giải »

Câu 15:

Cho hai số phức ${\mathrm{z}}_1=3+\mathrm{i},{\mathrm{z}}_2=-1+2\mathrm{i}$. Trong mặt phẳng tọa độ, điểm biểu diễn cho số phức $\mathrm{w}=2{\mathrm{z}}_1-{\mathrm{z}}_2$ là:

A. P(7;-1)

B. Q(5;-1)

C. M(7;0)

D. N(5;0)

Xem lời giải »

Câu 1:

Cho số phức $\mathrm{z}=\mathrm{a}+\mathrm{bi}\left(\mathrm{a},\mathrm{b}\in \mathrm{R}\right)$ thỏa mãn $3\mathrm{z}-\left(4+5\mathrm{i}\right)\overline{\mathrm{z}}=-17+11\mathrm{i}$. Tính ab

A. ab = 3

B. ab = 6

C. ab = -6

D. ab = -3

Xem lời giải »

Câu 2:

Cho số phức z thỏa mãn điều kiện $\left|\mathrm{z}-2+2\mathrm{i}\right|=1$. Tìm giá trị lớn nhất của $\left|\mathrm{z}\right|$

A. $\max \left|\mathrm{z}\right|=2\sqrt{2}+1$

B. $\max \left|\mathrm{z}\right|=2\sqrt{2}$

C. $\max \left|\mathrm{z}\right|=2\sqrt{2}+2$

D. $\max \left|\mathrm{z}\right|=2\sqrt{2}-1$

Xem lời giải »

Câu 3:

Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện $\left|\mathrm{z}-\mathrm{i}\right|=5$ và ${\mathrm{z}}^2$ là số thuần ảo?

A. 2

B. 3

C. 4

D. 0

Xem lời giải »

Câu 4:

Xét các số phức z thỏa mãn $\left|\mathrm{z}-1+2\mathrm{i}\right|=\sqrt{5}$. Tìm số phức w có mô đun lớn nhất, biết rằng $\mathrm{w}=\mathrm{z}+1+\mathrm{i}$

A. w = 4 - 2i

B. w = -2 + 4i

C. w = 4 - 3i

D. w = 4 + 3i

Xem lời giải »

Câu 5:

Cho các số phức ${\mathrm{z}}_1,{\mathrm{z}}_2$ thỏa mãn $\left|{\mathrm{z}}_1\right|=3,\left|{\mathrm{z}}_2\right|=4$ và $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=5$. Gọi A, B lần lượt là điểm biểu diễn các số phức ${\mathrm{z}}_1,{\mathrm{z}}_2$. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

A. S = 12

B. S = 6

C. S = $5\sqrt{2}$

D. S = $\frac{25}{2}$

Xem lời giải »

Câu 6:

Tập điểm biểu diễn số phức z thỏa mãn ${\left|\mathrm{z}\right|}^2={\mathrm{z}}^2$ là:

A. Cả mặt phẳng

B. Đường thẳng

C. Một điểm

D. Hai đường thẳng

Xem lời giải »

Câu 7:

Cho các số phức z thỏa mãn |z + 1 - i| = |z - 1 + 2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó

A. 4x + 6y - 3 = 0

B. 4x - 6y - 3 = 0

C. 4x + 6y + 3 = 0

D. 4x - 6y + 3 = 0

Xem lời giải »

Câu 8:

Có bao nhiêu số phức z thỏa mãn $\mathrm{z}-\overline{\mathrm{z}}={\mathrm{z}}^2$

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 9:

Gọi S là tổng phần thực và phần ảo của số phức $\mathrm{w}={\mathrm{z}}^3-\mathrm{i}$, biết z thỏa mãn $\mathrm{z}+2-4\mathrm{i}=\left(2-\mathrm{i}\right)\overline{\mathrm{iz}}$. Mệnh đề nào sau đây đúng?

A. S = -46

B. S = -36

C. S = -66

D. S = -1

Xem lời giải »

Câu 10:

Cho số phức $\mathrm{z}=1+\mathrm{i}+{\mathrm{i}}^2+{\mathrm{i}}^3+...+{\mathrm{i}}^9$. Khi đó:

A. z = i

B. z = 1 + i

C. z = 1 - i

D. z = 1

Xem lời giải »

Câu 11:

Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện $\left|\mathrm{z}\left(\mathrm{i}+1\right)-1-\mathrm{i}\right|=\sqrt{2}$

A. Đường thẳng x + y - 2 = 0

B. Đường tròn ${\mathrm{x}}^2+{\left(\mathrm{y}-1\right)}^2=1$

C. Cặp đường thẳng song song $\mathrm{y}=\pm 2$

D. Đường tròn ${\mathrm{y}}^2+{\left(\mathrm{x}-1\right)}^2=1$

Xem lời giải »

Câu 12:

Xét số phức z thỏa mãn |z + 2 - i +|z - 4 - 7i| = $6\sqrt{2}$. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z - 1 + i|. Tính P = m + M

A. $\mathrm{P}=\sqrt{13}+\sqrt{73}$

B. $\mathrm{P}=\frac{5\sqrt{2}+2\sqrt{73}}{2}$

C. $\mathrm{P}=5\sqrt{2}+\sqrt{72}$

D. $\mathrm{P}=\frac{5\sqrt{2}+\sqrt{73}}{2}$

Xem lời giải »

Câu 13:

Cho số phức z thỏa mãn $2\mathrm{iz}+\overline{\mathrm{z}}=1-\mathrm{i}$. Phần thực của số phức z là:

A. -2

B. 3

C. 1

D. -1

Xem lời giải »

Câu 14:

Tính mô đun của số phức z, biết z thỏa mãn $\left(1+2\mathrm{i}\right)\mathrm{z}+\left(2+3\mathrm{i}\right)\overline{\mathrm{z}}=6+2\mathrm{i}$

A. $\left|\mathrm{z}\right|=4$

B. $\left|\mathrm{z}\right|=2$

C. $\left|\mathrm{z}\right|=\sqrt{10}$

D. $\left|\mathrm{z}\right|=10$

Xem lời giải »

Câu 15:

Có bao nhiêu số phức thỏa mãn ${\mathrm{z}}^2+2\overline{\mathrm{z}}=0$?

A. 0

B. 1

C. 2

D. 4

Xem lời giải »

Câu 1:

Tính mô đun của số phức z biết $\overline{\mathrm{z}}=\left(4-3\mathrm{i}\right)\left(1+\mathrm{i}\right)$

A. $\left|\mathrm{z}\right|=25\sqrt{2}$

B. $\left|\mathrm{z}\right|=7\sqrt{2}$

C. $\left|\mathrm{z}\right|=5\sqrt{2}$

D. $\left|\mathrm{z}\right|=\sqrt{2}$

Xem lời giải »

Câu 2:

Biết rằng z là số phức có mô đun nhỏ nhất thỏa mãn $\left(1-\mathrm{z}\right)\left(\overline{\mathrm{z}}+2\mathrm{i}\right)$ là số thực. Số phức z là:

A. $\mathrm{z}=1+\frac{1}{2}\mathrm{i}$

B. $\mathrm{z}=\frac{3}{5}+\frac{4}{5}\mathrm{i}$

C. $\mathrm{z}=2\mathrm{i}$

D. $\mathrm{z}=\frac{4}{5}+\frac{2}{5}\mathrm{i}$

Xem lời giải »

Câu 3:

Tìm tập hợp các điểm biểu diễn số phức z, biết rằng số phức ${\mathrm{z}}^2$ có điểm biểu diễn nằm trên trục tung.

A. Trục tung

B. Trục hoành

C. Đường phân giác góc phần tư (I) và góc phần tư (III)

D. Đường phân giác góc phần tư (I), (III) và đường phân giác góc phần tư (II), (IV)

Xem lời giải »

Câu 4:

Cho số phức z thỏa mãn ${\left(1+\mathrm{z}\right)}^2$ là số thực. Tập hợp điểm M biểu diễn số phức z là:

A. Đường tròn

B. Đường thẳng

C. Hai đường thẳng

D. Một điểm duy nhất

Xem lời giải »

Câu 5:

Tập hợp các điểm trên mặt phẳng tọa độ Oxy biểu diễn số phức z thỏa mãn điều kiện: số phức $\mathrm{w}=\left(\mathrm{z}-\mathrm{i}\right)\left(2+\mathrm{i}\right)$ là một số thuần ảo là:

A. Đường thẳng ${\mathrm{x}}^2+{\mathrm{y}}^2=2$

B. Đường thẳng $\mathrm{x}+2\mathrm{y}-2=0$.

C. Đường thẳng $2\mathrm{x}-\mathrm{y}+1=0$.

D. Đường parabol $2\mathrm{x}={\mathrm{y}}^2$.

Xem lời giải »

Câu 6:

Cho số phức v = a + bi. Tập hợp các điểm trên mặt phẳng tọa độ Oxy biểu diễn số phức z thỏa mãn điều kiện $\left|\mathrm{z}-\mathrm{v}\right|=1$ là:

A. Đường tròn ${\left(\mathrm{x}-\mathrm{a}\right)}^2+{\left(\mathrm{y}-\mathrm{b}\right)}^2=1$

B. Đường thẳng y = b.

C.  Đường thẳng x = a.

D. Đường thẳng $\mathrm{x}+\mathrm{y}-\mathrm{a}-\mathrm{b}-1=0$

Xem lời giải »

Câu 7:

Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện $2\left|\mathrm{z}-\mathrm{i}\right|=\left|\mathrm{z}-\overline{\mathrm{z}}+2\mathrm{i}\right|$ là hình gì?

A. Một đường thẳng

B. Một đường parabol

C. Một đường elip

D. Đường tròn.

Xem lời giải »

Câu 8:

Tập hợp các điểm M biểu diễn số phức z thỏa mãn $\left|\mathrm{z}-\mathrm{i}\right|+\left|\mathrm{z}+\mathrm{i}\right|=4$ là:

A. Elip (E):$\frac{{\mathrm{x}}^2}{4}+\frac{{\mathrm{y}}^2}{3}=1$

B. Elip (E):$\frac{{\mathrm{x}}^2}{3}+\frac{{\mathrm{y}}^2}{4}=1$.

C. Elip (E): $\frac{{\mathrm{x}}^2}{4}+\frac{{\mathrm{y}}^2}{3}=4$.

D. Hình tròn tâm I (0; -1), bán kính R = 4

Xem lời giải »

Câu 9:

Cho số phức z thỏa mãn |z - 2 - 3i| = 1. Tìm giá trị lớn nhất của |z|

A. $1+\sqrt{13}$

B. $\sqrt{13}$.

C. $2+\sqrt{13}$.

D. $\sqrt{13}-1$.

Xem lời giải »

Câu 10:

Cho số phức z thỏa mãn $\left|\mathrm{z}-3-4\mathrm{i}\right|=1$. Mô đun lớn nhất của số phức z là:

A. 7

B. 6

C. 5

D. 4

Xem lời giải »

Câu 11:

Cho số phức z thỏa mãn $\left|\mathrm{z}-2-2\mathrm{i}\right|=1$. Số phức z - i có mô đun nhỏ nhất là:

A. $\sqrt{5}-1$

B. $1-\sqrt{5}$

C. $1+\sqrt{5}$

D. $2+\sqrt{5}$

Xem lời giải »

Câu 12:

Xác định số phức z thỏa mãn $\left|\mathrm{z}-2-2\mathrm{i}\right|=\sqrt{2}$ mà $\left|\mathrm{z}\right|$ đạt giá trị lớn nhất

A. z = 1 + i

B. z = 3 + i

C. z = 3 + 3i

D. z = 1 + 3i

Xem lời giải »

Câu 13:

Trong các số phức z thỏa mãn |z - 2 - 4i| = |z - 2i|. Tìm số phức z có mô đun nhỏ nhất

A. z = 2 - 2i

B. z = 1 + i

C. z = 2 + 2i

D. z = 1 - i

Xem lời giải »

Câu 14:

Cho số phức z có $\left|\mathrm{z}\right|=2$ thì số phức $\mathrm{w}=\mathrm{z}+3\mathrm{i}$ có mô đun nhỏ nhất và lớn nhất lần lượt là:

A. 2 và 5

B. 1 và 6

C. 2 và 6

D. 1 và 5

Xem lời giải »

Câu 15:

Cho số phức z thỏa mãn $\left|{\mathrm{z}}^2-\mathrm{i}\right|=1$. Tìm giá trị lớn nhất của |$\overline{\mathrm{z}}$|

A. 2

B. $\sqrt{5}$

C. $2\sqrt{2}$

D. $\sqrt{2}$

Xem lời giải »

Câu 1:

Cho số phức z có điểm biểu diễn nằm trên đường thẳng 3x - 4y - 3 = 0. |z| nhỏ nhất bằng

A. $\frac{1}{5}$

B. $\frac{3}{5}$

C. $\frac{4}{5}$

D. $\frac{2}{5}$

Xem lời giải »

Câu 2:

Cho số phức z thỏa mãn |z + 3| + |z - 3| = 10. Giá trị nhỏ nhất của |z| là:

A. 3

B. 4

C. 5

D. 6

Xem lời giải »

Câu 3:

Tìm tập hợp các điểm biểu diễn số phức z, biết rằng số phức ${\mathrm{z}}^2$ có điểm biểu diễn nằm trên trục hoành.

A. Trục tung

B. Trục hoành

C. Đường phân giác góc phần tư (I) và góc phần tư (III)

D. Trục tung và trục hoành

Xem lời giải »

Câu 4:

Cho ${\mathrm{z}}_1,{\mathrm{z}}_2$ thỏa mãn $\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|=1$ và $\left|{\mathrm{z}}_1+{\mathrm{z}}_2\right|=3$. Tính $\mathrm{maxT}=\left|{\mathrm{z}}_1\right|+\left|{\mathrm{z}}_2\right|$

A. 8

B. 10

C. 4

D. $\sqrt{10}$

Xem lời giải »

Câu 5:

Cho số phức ${\text{z}}_1$ thỏa mãn ${\left|{\mathrm{z}}_1-2\right|}^2-{\left|{\mathrm{z}}_1+\mathrm{i}\right|}^2=1$ và số phức ${\mathrm{z}}_2$ thỏa mãn $\left|{\mathrm{z}}_2-4-\mathrm{i}\right|=\sqrt{5}$. Tìm giá trị nhỏ nhất của $\mathrm{P}=\left|{\mathrm{z}}_1-{\mathrm{z}}_2\right|$

A. ${\mathrm{P}}_{\min }=\frac{2\sqrt{5}}{5}$

B. ${\mathrm{P}}_{\min }=\sqrt{5}$

C. ${\mathrm{P}}_{\min }=2\sqrt{5}$

D. ${\mathrm{P}}_{\min }=\frac{3\sqrt{5}}{5}$

Xem lời giải »

Câu 6:

Cho số phức $\mathrm{z}=-\frac{1}{2}+\frac{\sqrt{3}}{2}\mathrm{i}$. Số phức $1+\mathrm{z}+{\mathrm{z}}^2$ bằng:

A. 0

B. 1

C. $2-\sqrt{3}\mathrm{i}$

D. $-\frac{1}{2}+\frac{\sqrt{3}}{2}\mathrm{i}$

Xem lời giải »

Câu 7:

Biết rằng $\mathrm{z}={\mathrm{m}}^2-3\mathrm{m}+3+\left(\mathrm{m}-2\right)\mathrm{i}$$\left(\mathrm{m}\in \mathrm{R}\right)$ là một số thực. Giá trị của biểu thức $1+\mathrm{z}+{\mathrm{z}}^2+{\mathrm{z}}^3+...+{\mathrm{z}}^{2019}$ bằng:

A. 2019

B. 0

C. 1

D. 2020

Xem lời giải »

Câu 8:

Xét các số phức z thỏa mãn $\left(\mathrm{z}+2\mathrm{i}\right)\left(\overline{\mathrm{z}}+2\right)$ là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là:

A. (1; -1)

B. (1; 1)

C. (-1; 1)

D. (-1; -1)

Xem lời giải »

Câu 9:

Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện $\left|\mathrm{z}-2\right|+\left|\mathrm{z}+2\right|=10$

A. Đường tròn ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}+2\right)}^2=100$

B. Elipi: $\frac{{\mathrm{x}}^2}{25}+\frac{{\mathrm{y}}^2}{4}=1$

C. Đường tròn ${\left(\mathrm{x}-2\right)}^2+{\left(\mathrm{y}+2\right)}^2=10$ 

D. Elip: $\frac{{\mathrm{x}}^2}{25}+\frac{{\mathrm{y}}^2}{21}=1$

Xem lời giải »

Câu 10:

Trong mặt phẳng tọa độ, cho A, B, C là ba điểm biểu diễn lần lượt cho ba số phức ${\mathrm{z}}_1=5-\mathrm{i},{\mathrm{z}}_2={\left(4+\mathrm{i}\right)}^2$ và ${\mathrm{z}}_3=-8\mathrm{i}$. Diện tích tam giác ABC là kết quả nào dưới đây?

A. 25

B. $\frac{25}{2}$

C. $\frac{185}{2}$

D. 185

Xem lời giải »

Câu 11:

Cho hai số phức ${\mathrm{z}}_1,{\mathrm{z}}_2$ thỏa mãn $\left|{\mathrm{z}}_1\right|=6,\left|{\mathrm{z}}_2\right|=2$. Gọi M, N lần lượt là các điểm biểu diễn của số phức ${\mathrm{z}}_1$ và số phức ${\mathrm{iz}}_2$. Biết $\widehat{\mathrm{MON}}=60°$. Tính $\mathrm{T}=\left|{\mathrm{z}}_1^2+9{\mathrm{z}}_2^2\right|$

A. $\mathrm{T}=36\sqrt{2}$

B. $\mathrm{T}=36\sqrt{3}$

C. $\mathrm{T}=24\sqrt{3}$

D. T = 18

Xem lời giải »

Câu 12:

Cho số phức z thoả mãn $\left|\mathrm{z}-3+4\mathrm{i}\right|=2$ và $\mathrm{w}=2\mathrm{z}+1-\mathrm{i}$. Khi đó $\left|\text{w}\right|$ có giá trị lớn nhất là:

A. $16+\sqrt{74}$

B. $2+\sqrt{130}$

C. $4+\sqrt{74}$

D. $4+\sqrt{130}$

Xem lời giải »

Câu 13:

Cho số phức z thỏa mãn $\left|\mathrm{z}-1-2\mathrm{i}\right|=4$. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $\left|\mathrm{z}+2+\mathrm{i}\right|$. Tính $\mathrm{S}={\mathrm{M}}^2+{\mathrm{m}}^2$

A. S = 34

B. S = 82

C. S = 68

D. S = 36

Xem lời giải »

Câu 14:

Biết số phức thỏa mãn |iz - 3| = |z - 2 - i| và |z| có giá trị nhỏ nhất. Phần thực của số phức z bằng:

A. $\frac{2}{5}$

B. $\frac{1}{5}$

C. $\frac{-2}{5}$

D. $\frac{-1}{5}$

Xem lời giải »