Bài tập ôn tập chương I (mới nhất)

Câu 1:

Hàm số nào sau đây đồng biến trên tập số thực R?

A. y = x⁴ – 2x² – 5

B. y = - x + 1

C.

D. y = x³ + 3x – 1

Xem lời giải »

Câu 2:

Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?

$y=\frac{2x+1}{x+1}$(I) ; y = -x⁴ + x² – 2 (II); y = x³ – 3x – 5 (III).

A. I và II

B. Chỉ I

C. I và III

D. II và III

Xem lời giải »

Câu 3:

Cho hàm số

$f\left(x\right)=\frac{x^2-m}{x-1}$(m khác 1)

Chọn câu trả lời đúng

A. Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1

B. Hàm số luôn giảm trên tập xác định.

C. Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1

D. Hàm số luôn tăng trên (-∞;1) và (1;+∞)

Xem lời giải »

Câu 4:

Hàm số nào trong các hàm số sau đây đồng biến trên các khoảng (-∞;2) và (2;+∞) 

A. 

B .

C. 

D. 

Xem lời giải »

Câu 5:

Hàm số nào sau đây nghịch biến trên R.

A. y = -x³ + 2x² – x – 1

B. y = 1/3 x³ – x² + 3x + 1

C. y = -1/3.x³ + x² – x.

D. y = -x³ + 3x + 1

Xem lời giải »

Câu 6:

Hàm số nào sau đây đồng biến trên R.

A. 

B.

C. 

D. 

Xem lời giải »

Câu 7:

Hàm số nào sau đây nghịch biến trên R?

A. y = -x³ + 3x² + 3x – 2.

B. y = -x³ + 3x² – 3x – 2

C. y = x³ + 3x² + 3x – 2

D. y = x³ – 3x² – 3x – 2

Xem lời giải »

Câu 8:

Hàm số nào sau đây nghịch biến trên R?

A. y = -x³ + 3x² + 3x – 2

B. y = -x³ + 3x² – 3x – 2.

C. y = x³ + 3x² + 3x – 2

D. y = x³ – 3x² – 3x – 2.

Xem lời giải »

Câu 9:

Hàm số nào sau đây đồng biến trên R?

A. 

B.

C. 

D.

Xem lời giải »

Câu 10:

Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (-1;1)?

A. y = 1/x

B. y = x³ – 3x + 1

C. y = 1/x²

D. y = -1/x

Xem lời giải »

Câu 11:

Cho hàm số f(x) = -2x³ + 3x² – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?

A. Hàm số nghịch biến trên R

B. f(a) > f(b).

C. f(b) < 0

D. f(a) < f(b).

Xem lời giải »

Câu 12:

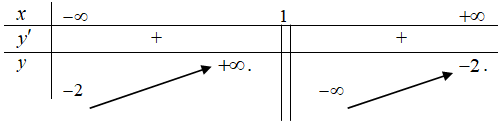
Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?

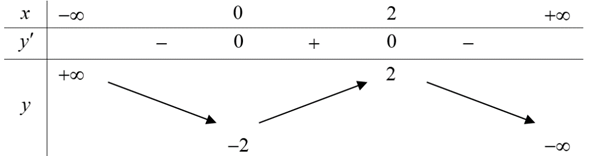
A. y = x³ – 3x² – 1

B. y = -x³ + 3x² – 2

C. y = -x³ + 3x² – 1

D. y = -x³ – 3x – 2

Xem lời giải »

Câu 13:

Cho hàm số y = f(x) = x³ + 3x. Hỏi khẳng định nào sau đây là khẳng định đúng?

A. Hàm số f(x) đồng biến trên R

B. Hàm số f(x) nghịch biến trên (-1;0)

C. Hàm số f(x) nghịch biến trên (-∞;0).

D. Hàm số f(x) không đổi trên R

Xem lời giải »

Câu 14:

Đâu là hàm số đồng biến trên đoạn [2;5]?

A. y = x

B. y = x(x+1)(x+2)

C. y = x(x+1)(x+2)(x+3)(x+4)

D. Cả A, B và C đều đúng

Xem lời giải »

Câu 15:

Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng 

A.

B. 

C. 

D.

Xem lời giải »

Câu 16:

Tìm tất cả các giá trị thực của tham số m đề hàm số $y =\frac{x}{x-m}$ nghịch biến trên khoảng (1;+∞)

A. 0 < m ≤ 1

B. 0 < m < 1

C. m > 1

D. 0 ≤ m < 1

Xem lời giải »

Câu 17:

Với giá trị nào của m thì hàm số $y=\frac{mx+4}{x+m}$ đồng biến trên khoảng (1;+∞)

A.$-2<m<2$

B.

C.m>2

D.m<-2

Xem lời giải »

Câu 18:

Tìm tất cả giá trị của m để hàm số $y=\frac{(m+1)x-2}{x-m}$đồng biến trên từng khoảng xác định 

A.

B. 

C.

D.

Xem lời giải »

Câu 19:

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số $y=\frac{1}{3}{x}^3-2x^2+3x-5$ là đường thẳng

A. song song với đường thẳng x = 1

B. song song với trục hoành

C. có hệ số góc dương.

D. có hệ số góc bằng -1

Xem lời giải »

Câu 20:

Đồ thị của hàm số y = x⁴ – x² + 1 có bao nhiêu điểm cực trị có tung độ dương?

A. 1

B. 2.

C. 3.

D. 4

Xem lời giải »

Câu 21:

Khẳng định nào sau đây là khẳng định sai về hàm số $y=\frac{2x-1}{x+1}$

A. Hàm số đồng biến trên (1; +∞)

B. Hàm số đồng biến trên từng khoảng xác định.

C. Hàm số có cực trị

D. Hàm số đồng biến trên (-∞;-1)

Xem lời giải »

Câu 22:

Cho hàm số y = 2x³ + 3x² – 12x - 12. Gọi x₁, x₂ lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?

A. (x₁ – x₂)² = 8

B. x₁x₂ = 2

C. x₂ – x₁ = 3

D. x₁² + x₂² = 6

Xem lời giải »

Câu 23:

Hỏi hàm số y = x³ – 3x² – 9x – 2 đạt cực tiểu tại điểm nào?

A. x = -3

B. x = -1

C. x = 1

D. x = 3

Xem lời giải »

Câu 24:

Tìm tất cả các điểm cực đại của hàm số y = -x⁴ + 2x² + 1

A. x = ±1

B. x = -1

C. x = 1

D. x = 0

Xem lời giải »

Câu 25:

Hàm số nào dưới đây không có cực trị?

A. y = x⁴ + x²

B. y = x² - 1

C. y = x³ – x²

D. y = x³ + 3x

Xem lời giải »

Câu 26:

x = 2 không phải là điểm cực đại của hàm số nào sau đây? 

A. 

B.

C.

D.

Xem lời giải »

Câu 27:

Tìm tất cả các điểm cực trị của hàm số y = 1/2.sin 2x + cos x – 2017

A.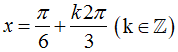 

B.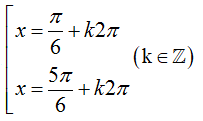  

C.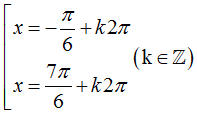 

D.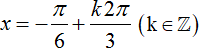 

Xem lời giải »

Câu 28:

Gọi x₁, x₂ là hai điểm cực trị của hàm số $y=\frac{x^2-4x}{x+1}$Tính giá trị của biểu thức P = x₁.x₂

A. P = -5

B. P = -2

C. P = -1

D. P = -4

Xem lời giải »

Câu 29:

Cho hàm số  $y=\frac{1}{2}x-\sqrt{x}$ tìm khẳng định đúng?

A. Hàm số đã cho có đạt cực tiểu duy nhất là y = 1

B. Hàm số đã cho đạt cực đại duy nhất là y = -1/2

C. Hàm số đã cho chỉ có giá trị cực tiểu là y = -1/2

D. Hàm số đã cho không có cực trị

Xem lời giải »

Câu 30:

Cho hàm số y = f(x) có đạo hàm trong khoảng (a, b) chứa điểm x₀ (có thể trừ điểm x₀). Tìm mệnh đề đúng trong các mệnh đề sau:

A. Nếu f(x) không có đạo hàm tại x₀ thì f(x) không đạt cực trị tại x₀

B. Nếu f’(x₀) = 0 thì f(x) đạt cực trị tại điểm x₀

C. Nếu f’(x₀) = 0 và f’’(x₀) = 0 thì f(x) không đạt cực trị tại điểm x₀

D. Nếu f’(x₀) = 0 và f’’(x₀) ≠ 0 thì f(x) đạt cực trị tại điểm x₀

Xem lời giải »

Câu 1:

Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) = (x – 1)x²(x + 1)³(x + 2)⁴. Hỏi hàm số có bao nhiêu điểm cực trị?

A. 4.

B. 1

C. 2

D. 3

Xem lời giải »

Câu 2:

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

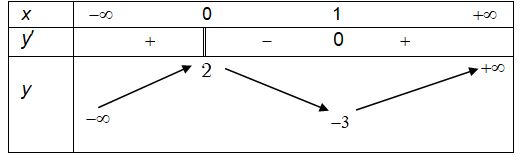
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Xem lời giải »

Câu 3:

Cho hàm số y = mx⁴ – (m² – 1)x² + 1. Khẳng định nào sau đây là sai?

A. Với m = 0 thì hàm số có một điểm cực trị

B. Hàm số luôn có 3 điểm cực trị với với mọi m ≤ 0

C. Với m ∈ (-1;0) ∪ (1;+∞) hàm số có 3 điểm cực trị

D. Có nhiều hơn ba giá trị của tham số m để hàm số có 1 điểm cực trị

Xem lời giải »

Câu 4:

Cho các phát biểu sau:

I. Đồ thị hàm số có y = x⁴ – x + 2 có trục đối xứng là Oy.

II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x₀ thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x₀,f(x₀)) song song với trục hoành.

III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).

IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x₀ thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x₀) và đồng biến trên khoảng (x₀;b).

Các phát biểu đúng là:

A. II,III,IV

B. I,II,III

C. III,IV

D. I,III,IV

Xem lời giải »

Câu 5:

Hàm số nào trong các hàm số sau đây không có cực trị?

A. y = |x|.

B. y = x³ – x² + 3x + 5

C. y = x⁴ + x² – 2

D. y = 3x² + 2x – 1

Xem lời giải »

Câu 6:

Hàm số y = x⁴ – 4x² + 4 đạt cực tiểu tại những điểm nào? 

A. x = ± √2, x = 0

B. x = ± √2

C. x = √2, x = 0

D. x = - √2

Xem lời giải »

Câu 7:

Cho hàm số $y=\frac{1}{3}{x}^3+x^2-7x+3$ đạt cực trị tại x₁, x₂.Tính T = x₁³ + x₂³

A. T = -50

B. T = -30

C. T = 29

D. T = 49

Xem lời giải »

Câu 8:

Kết luận nào đúng về cực trị của hàm số y = x³ – 3x² + 3x + 4

A. Đạt cực đại tại x = 1

B. Có hai điểm cực trị

C. Đạt cực tiểu tại x = 1

D. Không có cực trị

Xem lời giải »

Câu 9:

Hàm số y = x – sin 2x + 3. Chọn khẳng định đúng trong các khẳng định sau?

A. Nhận điểm x = -π/6 làm điểm cực tiểu

B. Nhận điểm x = π/2 làm điểm cực đại

C. Nhận điểm x =  -π/6 làm điểm cực đại

D. Nhận điểm x = π/2 làm điểm cực tiểu

Xem lời giải »

Câu 10:

Hàm số y = x³ – 3x² + 3x – 4 có bao nhiêu cực trị?

A. 0

B. 1

C. 2.

D. 3

Xem lời giải »

Câu 11:

Cho hàm số y = -x³ + 3x² – 3x + 1, mệnh đề nào sau đây là đúng?

A. Hàm số đạt cực đại tại x = 1

B. Hàm số luôn luôn nghịch biến

C. Hàm số luôn luôn đồng biến

D. Hàm số đạt cực tiểu tại x = 1

Xem lời giải »

Câu 12:

Số điểm cực đại của đồ thị hàm số y = x⁴ + 100 là:

A. 1.

B. 3.

C. 0

D. 2.

Xem lời giải »

Câu 13:

Tìm x_CĐ (nếu có) của hàm số $y=\sqrt{x-3}-\sqrt{6-x}$

A. x_CĐ = 3

B. x_CĐ = 6

C. x_CĐ = 0

D. Hàm số không có điểm cực đại

Xem lời giải »

Câu 14:

Cho hàm số $y=\frac{-x^2+3}{x-2}$. Mệnh đề nào dưới đây đúng?

A. Cực tiểu của hàm số bằng -2

B. Cực tiểu của hàm số bằng 3

C. Cực tiểu của hàm số bằng 1

D. Cực tiểu của hàm số bằng -6

Xem lời giải »

Câu 15:

Tìm số điểm cực trị của hàm số y = x⁴ + 2x² + 3

A. 0

B. 1

C. 2

D. 3

Xem lời giải »

Câu 16:

Hàm số y = x – sin 2x đạt cực đại tại các điểm nào cho dưới đây?

A. x = -π/3 + kπ, k ∈ Z.

B. x = π/3 + kπ, k ∈ Z.

C. x = π/6 + kπ, k ∈ Z.

D. x = -π/6 + kπ, k ∈ Z.

Xem lời giải »

Câu 17:

Cho hàm số $y=\frac{x^2-4x+8}{x-2}$ Số điểm cực trị của hàm số là

A. 0.

B. 1.

C. 3.

D. 2.

Xem lời giải »

Câu 18:

Tọa độ điểm cực đại của đồ thị hàm số y = x³ – 3x² + 4 là:

A. (2;4)

B. (2;0)

C. (0;-4)

D. (0;4) 

Xem lời giải »

Câu 19:

Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Tính tổng x₁ + y₁

A. 5.

B. -11

C. 7

D. 6

Xem lời giải »

Câu 20:

Tìm độ dài khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x³ + 3x² – 4?

A. 2√5

B. 4√5

C. 6√5

D. 8√5

Xem lời giải »

Câu 21:

Đồ thị của hàm số y = 3x⁴ – 4x³ – 6x² + 12x + 1 đạt cực tiểu tại M(x₁; y₁). Khi đó x₁ + y₁ bằng

A. 5

B. 6

C. -11

D. 7

Xem lời giải »

Câu 22:

Đồ thị hàm số y = ax³ + bx² + cx + d có hai điểm cực trị A(0;0), B(1;1) thì các hệ số a, b, c, d có giá trị lần lượt là:

A. a = -2; b = 1; c = 0; d = 0

B. a = 0; b = 0; c = -2; d = 3.

C. a = -2; b = 0; c = 3; d = 0

D. a = -2; b = 3; c = 0; d = 0

Xem lời giải »

Câu 23:

Điểm cực đại của đồ thị hàm số y = x³ + 3x² + 2 là

A. (2;0).

B. (0;2).

C. (-2;6).

D. (-2;-18).

Xem lời giải »

Câu 24:

Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)²

A. 5$\sqrt{2}$

B. 2

C. 2$\sqrt{5}$

D. 4

Xem lời giải »

Câu 25:

Tìm tất cả giá trị của m để hàm số y = 1/3.x³ – mx² + (m² – m + 1)x + 1 đạt cực đại tại x = 1

A. m = -2

B. m = -1

C. m = 2.

D. m = 1

Xem lời giải »

Câu 26:

Đồ thị hàm số y = x⁴ – 3x² + ax + b có điểm cực tiểu A(2;-2). Tính tổng (a + b)

A. -14

B. 14

C. -20

D. 34

Xem lời giải »

Câu 27:

Cho hàm số $y=\frac{x^2+3}{x-1}$ Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực tiểu tại x = -1

B. Hàm số có hai cực trị y_CĐ < y_CT

C. Hàm số đạt cực đại tại x = 3

D. Giá trị cực tiểu bằng -2

Xem lời giải »

Câu 28:

Cho hàm số y = x³/3 – 2x² + 3x + 2/3. Toạ độ điểm cực đại của đồ thị hàm số là

A. (-1;2)

B. (3;2/3).

C. (1;-2)

D. (1;2)

Xem lời giải »

Câu 29:

Giá trị lớn nhất của hàm số $y=\sqrt{-x^2+4x}$là:

A. 4

B. 0

C. -2

D. 2

Xem lời giải »

Câu 30:

Hàm số $y=\frac{x^2-4x+1}{x+1}$có hai điểm cực trị là x₁, x₂, khi đó tích x₁x₂ bằng

A. -5.

B. 5.

C. -2.

D. 2.

Xem lời giải »

Câu 1:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\sqrt{-x^2+6x-5}$ trên đoạn [1;5] lần lượt là

A. 2 và 0

B. 4 và 0

C. 3 và 0

D. 0 và -2

Xem lời giải »

Câu 2:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right)=2x-4\sqrt{6-x}$trên đoạn [-3;6]. Tổng M + m có giá trị là

A. 18

B. -6

C. -12

D. -4

Xem lời giải »

Câu 3:

Hàm số $y=\sqrt{4-x}-\sqrt{x+6}$ đạt giá trị nhỏ nhất tại x = x₀. Tìm x₀

A. x₀ = -6

B. x₀ = -1

C. x₀ = 0  ­

D. x₀ = 4

Xem lời giải »

Câu 4:

Hàm số $y=4\sqrt{x^2-2x+3}+2x-x^2$ đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là

A. 2

B. 1

C. 0.

D. -1

Xem lời giải »

Câu 5:

Giá trị nhỏ nhất của hàm số $y=\sqrt{6-x}-\sqrt{x+4}$ đạt tại x₀, tìm x₀?

A. x₀ = -√10

B. x₀ = -4

C. x₀ = 6

D. x₀ = √10

Xem lời giải »

Câu 6:

Cho hàm số $y=5\sqrt{3-x}$ Tìm giá trị nhỏ nhất của hàm số.

A. 3

B. 5

C. 0

D. 1

Xem lời giải »

Câu 7:

Tìm giá trị m để hai đường tiệm cận của đồ thị hàm số $y=\frac{mx+2}{3-2x}$( m khác $-\frac{4}{3}$)tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 1/5 

A. m = ±4/15.

B. m = ±15/4

C. m = 14/5

D. m = -14/5

Xem lời giải »

Câu 8:

Cho hàm số y = ax⁴ + bx² + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

A. a > 0, b< 0, c > 0

B. a < 0, b > 0, c < 0

C. a < 0, b< 0, c < 0

D. a > 0, b< 0, c < 0

Xem lời giải »

Câu 9:

Tìm m để hàm số y = x⁴ – 2mx² + 2m + m⁴ – 5 đạt cực tiểu tại x = -1

A. m = -1

B. m ≠ 1

C. m = 1

D. m ≠ -1

Xem lời giải »

Câu 10:

Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên

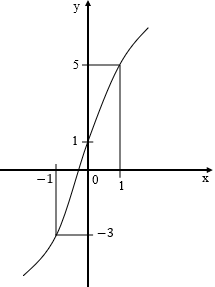
A. y = x³ + 3x + 1

B. y = x³ – 3x + 1

C. y = -x³ – 3x + 1

D. y = -x³ + 3x + 1

Xem lời giải »

Câu 11:

Cho hàm số y = f(x) xác định và liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?

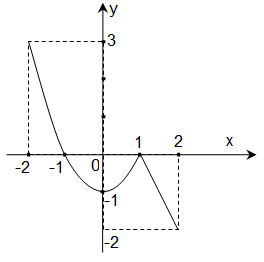
A. x = - 2

B. x = 0

C. x = 1

D. x = 2

Xem lời giải »

Câu 12:

Đường cong trong hình bên là đồ thị của hàm số nào sau đây?

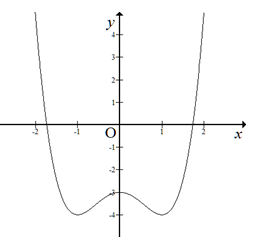
A. y = x⁴ – 2x² – 3

B. y = x⁴ + 8x² – 9

C. y = -x⁴ + 2x² – 3

D. y = x⁴ + 2x² – 3

Xem lời giải »

Câu 13:

Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

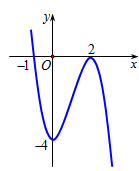
A. y = -x³ – 4

B. y = x³ – 3x² – 4

C. y = -x³ + 3x² – 4

D. y = -x³ + 3x² – 2.

Xem lời giải »

Câu 14:

Cho hàm số y = -x³ + 6x² – 4. Mệnh đề nào dưới đây sai?

A. Hàm số đạt cực trị tại x = 0

B. Hàm số nghịch biến trên khoảng (-∞;1)

C. Hàm số đồng biến trên khoảng (0;4)

D. Đồ thị hàm số có 2 điểm cực trị

Xem lời giải »

Câu 15:

Bảng biến thiên sau đây là của hàm số nào?

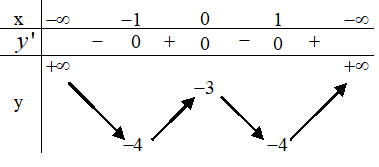
A. y = x⁴ – 3x² – 3

B. y = -x⁴ + 2x² – 3

C. y = x⁴ + 2x² – 3

D. y =x⁴ – 2x² – 3

Xem lời giải »

Câu 16:

Bảng biến thiên sau đây là của hàm số nào?

A. 

B. 

C. 

D. 

Xem lời giải »

Câu 17:

Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

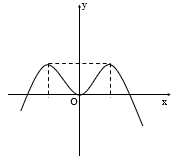
A. y = -x⁴ – 2x²

B. y = x⁴ – 2x²

C. y = x⁴ + 2x²

D. y = -x⁴ + 2x²

Xem lời giải »

Câu 18:

Hình ảnh bên là đồ thị của hàm số nào sau đây?

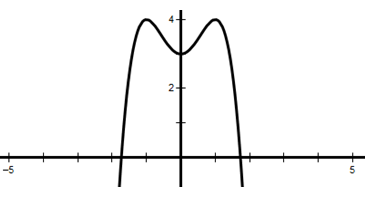
A. y = x⁴ – 2x² – 3

B. y = x⁴ + 2x² – 3

C. y = -x⁴ + 2x² + 3

D. y = -x⁴ – 2x² + 3

Xem lời giải »

Câu 19:

Đồ thị hình bên là của hàm số nào? Chọn một khẳng định ĐÚNG

A. 

B. 

C. 

D. 

Xem lời giải »

Câu 20:

Bảng biến thiên sau là của hàm số nào?

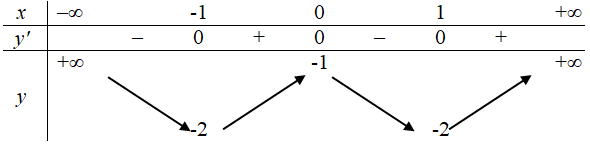
A. y = x⁴ – 2x² + 1

B. y = x⁴ – 2x² – 1

C. y = x⁴ – x² – 1

D. y = -x⁴ + 2x² – 1

Xem lời giải »

Câu 21:

Cho biết hàm số y = ax³ + bx² + cx + d có đồ thị như hình vẽ bên. Trong các khẳng định sau, khẳng định nào đúng?

A. 

B. 

C. 

D. 

Xem lời giải »

Câu 22:

Cho hàm số có bảng biến thiên ở hình bên. Khẳng định nào sau đây là khẳng định sai? 

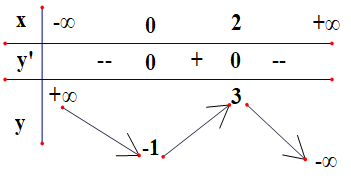
A. Hàm số có 2 cực trị

B. Hàm số có giá trị cực đại bằng 3

C. Hàm số có giá trị lớn nhất bằng 3, giá trị nhỏ nhất bằng -1

D. Hàm số đạt cực tiểu tại x = 0

Xem lời giải »

Câu 23:

Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

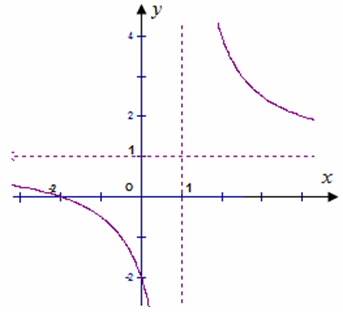
A. 

B. 

C. 

D. 

Xem lời giải »

Câu 24:

Đường cong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số đó là hàm số nào?

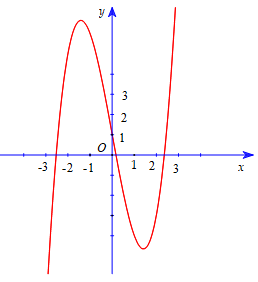
A. y = -x³ – 3x + 1

B. y = x² – 6x + 1

C. y = x³ – 6x + 1

D. y = x⁴ – 3x² + 1

Xem lời giải »

Câu 25:

Đồ thị sau đây là của hàm số nào?

A. $y=\frac{2x-1}{x+1}$

B. 

C. 

D. 

Xem lời giải »

Câu 26:

Đường cong trong hình là đồ thị của một trong 4 hàm số được cho bởi các phương án A, B, C, D dưới đây. Hỏi đó là hàm số nào

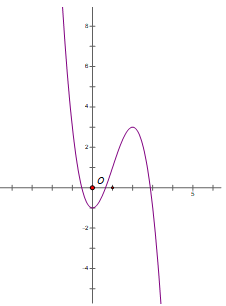
A. y = x⁴ – x² + 1

B. y = x³ – 3x² + 1

C. y = -x³ + 3x² – 1

D. y = x² – 4x + 3

Xem lời giải »

Câu 27:

Đồ thị sau đây là của hàm số nào?

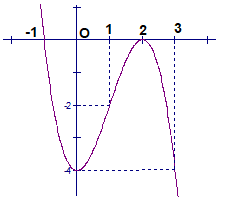
A. y = x³ – 3x – 4

B. y = -x³ + 3x² - 4

C. y = x³ – 3x – 4

D. y = -x³ – 3x² - 4

Xem lời giải »

Câu 28:

Tìm các giá trị của tham số m để hàm số y =  $\frac{1}{3}{x}^3$– x² + (m² – 4)x + 11 đạt cực tiểu tại x = 3

A. m = -1

B. m = 1

C. m = {-1;1}

D. m = 0.

Xem lời giải »

Câu 29:

Cho hàm số $y=\frac{ax+b}{cx+d}$ với a > 0 có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

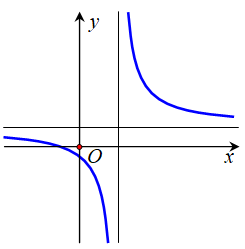
A. b > 0, c < 0, d < 0.

B. b > 0,  c > 0, d < 0

C. b < 0,  c > 0, d < 0

D. b < 0, c < 0, d < 0

Xem lời giải »

Câu 30:

Đồ thị (C) của hàm số $y=\frac{2x-8}{x}$ cắt đường thẳng Δ: y = -x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB

A. I(-1;1).

B. I(-2;2).

C. I(3;-3).

D. I(6;-6).

Xem lời giải »

Câu 1:

Biết rằng đồ thị hàm số  $y=\frac{x+3}{x-1}$và đường thẳng y = x – 2 cắt nhau tại hai điểm phân biệt A(x_A;y_A) và B(x_B;y_B). Tính y_A + y_B.

A. y_A + y_B = -2

B. y_A + y_B = 2

C. y_A + y_B = 4

D. y_A + y_B = 0

Xem lời giải »

Câu 2:

Tung độ giao điểm của đồ thị các hàm số y = x³ – 3x² + 2, y = -2x + 8 là:

A. 2

B. 4

D. 0

D. 6

Xem lời giải »

Câu 3:

Có bao nhiêu điểm M thuộc đồ thị hàm số $y=\frac{x+2}{x-1}$ sao cho khoảng cách từ M đến trục tung bằng hai lần khoảng cách từ M đến trục hoành

A. 3

B. 2

C. 0

D. 1

Xem lời giải »

Câu 4:

Cho hàm số $y=\frac{2x+1}{x-1}$ Khẳng định nào sau đây là khẳng định sai?

A. Đồ thị hàm số cắt Oy tại điểm (0;2)

B. Đồ thị hàm số có tâm đối xứng I(1;2)

C. Đồ thị hàm số có tiệm cận đứng x = 1

D. Đồ thị hàm số có tiệm cận ngang y = 2

Xem lời giải »

Câu 5:

Tìm tọa độ tâm đối xứng của đồ thị hàm số y = x³ +3x² - 9x +1

A. (-1;6)

B. (-1;12)

C. (1;4)

D. (-3;28) 

Xem lời giải »

Câu 6:

Hàm số y = mx⁴ + (m + 3)x² + 2m – 1 chỉ đạt cực đại mà không có cực tiểu với m

A. m > 3 .

B. m ≤ -3  

C. m ≤ 0 hoặc m >3  

D. -3 < m < 0

Xem lời giải »

Câu 7:

Cho hàm số y = mx⁴ – (m – 1)x² – 2. Tìm tất cả các giá trị thực của m để đồ thị hàm số có ba điểm cực trị

A. m ≤ 1

B. 0 < m < 1

C. m > 0

D. m  (- ∞;0)∪ (1;+∞)

Xem lời giải »

Câu 8:

Hàm số y = (m – 3)x³ – 2mx² + 3 không có cực trị khi

A. m = 3

B. m = 0 hoặc m  = 3 

C. m = 0

D. m ≠ 3

Xem lời giải »

Câu 9:

Hàm số y = 2x⁴ – (m² – 4)x² + 3 có 3 cực trị khi:

A. m > 2; m < -2

B. -2 < m < 2

C. m < 0

D. m > 1

Xem lời giải »

Câu 10:

Cho hàm số y = x³ + ax² + bx + c đi qua điểm A(0;-4) và đạt cực đại tại điểm B(1;0) hệ số góc k của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng -1 là:

A. k = 0

B. k = 24

C. k = -18

D. k = 18

Xem lời giải »

Câu 11:

Cho hàm số y = f(x) = -x³ + (2m – 1)x² – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu?

A. m ∈ (-1; +∞)

B. m ∈ (-1; 5/4)

C. m ∈ (-∞; -1)

D. m ∈ (-∞; -1) ∪ (5/4; +∞)

Xem lời giải »

Câu 12:

Đồ thị hàm số $y=\frac{x^2+mx-2}{mx-1}$ có các điểm cực đại, cực tiểu có hoành độ dương khi m thỏa mãn:

A. m > 2

B. 0 < m < 2

C. -2 < m < 0

D. 0 < m < 1

Xem lời giải »

Câu 13:

Tìm tất cả các giá trị của m để hàm số y =  x³/3 – (m + 1)x²  + (m² – 3)x – 1 đạt cực trị tại x = -1

A. m = 0

B. m = -2

C. m = 0; m = -2

D. m = 0; m = 2

Xem lời giải »

Câu 14:

Cho hàm số y = f(x) = x³ – 3x² + m,∀m ∈ R. Tìm tham số m để hàm số có giá trị cực đại bằng 2

A. m = 2

B. m = -2

C. m = -4

D. m = 0

Xem lời giải »

Câu 15:

Tìm tất cả các giá trị của tham số m để hàm số y = -x³ + 2x² + mx đạt cực đại tại x = 1

A. m = -1

B. m > -1

C. m ≠ -1

D. m < -1

Xem lời giải »

Câu 16:

x = 2 không phải là điểm cực đại của hàm số nào sau đây?

A. $y=\frac{x^2+x-1}{x-1}$

B. y = -x² + 4x – 1.

C. y = x³/3 – 3x² + 8x – 1

D. y = -x⁴/4  + 2x² + 1

Xem lời giải »

Câu 17:

Hàm số y = x³/3 – (m + 1)x² + (2m² + 1)x + m đạt cực tiểu tại x = 1 khi

A. m = 0

B. m = 1

C. A và B đúng

D. A và B sai

Xem lời giải »

Câu 18:

Tập hợp tất cả các giá trị của tham số thực m sao cho hàm số $y=\frac{x^2+x+m^2}{x+1}$ đạt cực đại tại x = 1 là

A. {∅ }.

B. {2}.

C. {2;-2}.

D. {-2}.

Xem lời giải »

Câu 19:

Giá trị của m để hàm số f(x) = x³ – 3x² + 3(m² – 1)x đạt cực tiểu tại x₀ = 2 là:

A. m = 1

B. m = -1

C. m ≠ ±1

D. m = ±1

Xem lời giải »

Câu 20:

Cho hàm số $y=\frac{1}{3}\sin 3x+m\sin x$ Tìm tất cả các giá trị của m để hàm số đạt cực đại tại điểm x = π/3

A. m > 0

B. m = 0

C. m = 1/2 

D. m = 2

Xem lời giải »

Câu 21:

Hàm số $y=\frac{x^2+3}{x+1}$  nghịch biến trên khoảng nào?

A. (-3;1).

B. (1; +∞).

C. (-∞; -3).

D. (-3; -1) và (-1; 1)

Xem lời giải »

Câu 22:

Hàm số y = x⁴ – 2x² + 3 đồng biến trên các khoảng nào?

A. R

B. (-1 ; 0) và (0 ; 1).

C. (-∞; -1) và (0 ; 1).

D. (-1 ;0) và (1; +∞)

Xem lời giải »

Câu 23:

Hàm số y = x³ – 3x² + 3x + 2017

A. Đồng biến trên TXĐ

B. Nghịch biến trên tập xác định

C. Đồng biến trên (1; +∞).

D. Đồng biến trên (-5; +∞)

Xem lời giải »

Câu 24:

Cho hàm số y = - x³ – x² + 5x + 4. Mệnh đề nào sau đây đúng?

A. Hàm số nghịch biến trên (-5/3 ; 1)

B. Hàm số đồng biến trên (-5/3 ; 1)

C. Hàm số đồng biến trên (-∞; -5/3 ).

D. Hàm số đồng biến trên (1; +∞)

Xem lời giải »

Câu 25:

Các khoảng đồng biến của hàm số y = x³ – 3x² + 2 là :

A. (-∞; 0).

B. (0; 2).

C. (-∞; 0)∪(2; +∞).

D. (-∞; 0) và (2; +∞)

Xem lời giải »

Câu 26:

Hỏi hàm số y = 2x³ + 3x² + 5 nghịch biến trên khoảng nào?

A. (-∞; -1)

B. (-1; 0)

C. (0; +∞)

D. (-3; 1)

Xem lời giải »

Câu 27:

Hàm số y = x⁴ – 2x² – 1 đồng biến trên khoảng nào sau đây:

A. (-∞; -1) và (0; 1)

B. (-1; 0) và (0; 1)

C. (-1;0) và (1; +∞)

D. Đồng biến trên R

Xem lời giải »

Câu 28:

Hàm số y = x³ – 3x² nghịch biến trên khoảng nào dưới đây?

A. (-1;1).

B. (-∞; 1).

C. (0; 2).

D. (2; +∞).

Xem lời giải »

Câu 29:

Cho hàm số y = x⁴ – 8x² – 4. Các khoảng đồng biến của hàm số là:

A. (-2;0) và (2; +∞)

B. (-2; 0) và (0; 2)

C. (-∞; -2) và (0; 2).

D. (-∞; -2) và (2; +∞)

Xem lời giải »

Câu 30:

Cho hàm số $y=\frac{3-x}{x+1}$Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên mỗi khoảng (-∞; -1) và (-1; +∞)

B. Hàm số nghịch biến với mọi x ≠ 1

C. Hàm số nghịch biến trên tập R \ {-1}

D. Hàm số nghịch biến trên mỗi khoảng (-∞; -1) và (-1; +∞)

Xem lời giải »

Câu 1:

Tìm tất các giá trị thực của tham số m  để hàm số $y=\frac{1}{3}{x}^3+(m+3)x^2+4(m+3)x+m^3-m$ đạt cực trị tại $x_1,x_2$ thỏa mãn -2<$x_1<x_2$

A. m< -2.

B. m< 1.

C. m< -3

D. m>3

Xem lời giải »

Câu 2:

Tìm các giá trị của tham số m để hàm số: $y=\frac{1}{3}m{x}^3-(m-1)x^2+3\left(m-2\right)x+\frac{1}{6}$

đạt cực trị tại $x_1<x_{2 }thỏa mãn 4x_1+3x_2=3$

A. $1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$

B. 1<m<2

C. 2< m<3

D. Đáp án khác

Xem lời giải »

Câu 3:

Cho hàm số y= f(x) =ax³+ bx²+cx+d  có đạo hàm là hàm số y= f’ (x)  với đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y= f( x)  tiếp xúc với trục hoành tại điểm có hoành độ dương . Khi đó đồ thị hàm số y= f( x)  cắt trục tung tại điểm có tung độ là bao nhiêu?

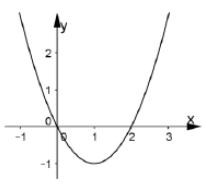
A. 2/3

B. 1

C. 3/2

D. 4/3

Xem lời giải »

Câu 4:

Giá trị lớn nhất của hàm số $y=\sqrt{x+4}+\sqrt{4-x}-4\sqrt{\left(x+4\right)\left(4-x\right)}+5$  bằng

A. $\underset{[-4;4]}{max}y=10$

B. $\underset{[-4;4]}{max}y=5-2\sqrt{2}$

C. $\underset{[-4;4]}{max}y=-7$

D. $\underset{[-4;4]}{max}y=5+2\sqrt{2}$

Xem lời giải »

Câu 5:

Cho hàm số y= 2x³-3x²+1  có đồ thị và đường thẳng  d: y=x-1. Giao điểm của (C)  và d  lần lượt là A( 1; 0); B và C. Khi đó khoảng cách giữa B và C  là

A. BC=$\frac{\sqrt{30}}{2}$

B.  BC=$\frac{\sqrt{34}}{2}$

C.  BC=$\frac{3\sqrt{2}}{2}$

D.  BC=$\frac{\sqrt{14}}{2}$

Xem lời giải »

Câu 6:

Giá trị nhỏ nhất của hàm số y= 2sin⁴x+ cos²x+ 3  bằng

A. 5

B. 6

C. 4

D. tất cả sai

Xem lời giải »

Câu 7:

Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số y= 2sin⁸ x+ cos⁴2x. Khi đó M + m bằng

A. 28/27

B. 4.

C. 82/27

D. 2.

Xem lời giải »

Câu 8:

Tìm m  để đồ thị hàm số  y = x³+mx+2 cắt trục hoành tại một điểm duy nhất.

A.m > 1

B. m > 2

C. m > -3

D. m < -2

Xem lời giải »

Câu 9:

Hàm số $y=\sqrt{1-x}+\sqrt{x+3}+\sqrt{1-x}.\sqrt{x+3}$  có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:

A. $2\sqrt{2}-2; 2.$

B. $2\sqrt{2}+2; 2.$

C. $2\sqrt{2}; 2.$

D. 2; 0.

Xem lời giải »

Câu 10:

Cho f(x) =$(m^4+1)x^4+(-2^{m+1}.m^2-4)x^2+4^m+16$. Số cực trị của hàm số y = |f(x)-1|  là:

A. 2

B. 4

C. 3

D. 5

Xem lời giải »

Câu 11:

Cho hàm số y = ax³+ bx²+ cx+ d  có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax³+ bx²+ cx+ d + 1| có bao nhiêu điểm cực trị?

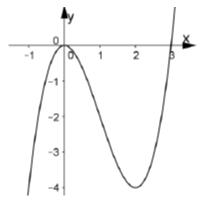
A. 2

B. 3

C. 5

D. 4

Xem lời giải »

Câu 12:

Hàm số  $y=\sqrt{x+2}+\sqrt{2-x}+2\sqrt{4-x^2}$ đạt giá trị lớn nhất, giá trị nhỏ nhất tại điểm có hoành độ là:

A. $2\sqrt{2}+4; 2.$

B. $2\sqrt{2}-2; 2.$

C. $2\sqrt{2}; 2.$

D. 4; 2

Xem lời giải »

Câu 13:

Cho hàm số  $y=\frac{mx-1}{x+2}$ có đồ thị là (C) . Tìm m để đường thẳng d: y=2x-1 cắt đồ thị (C)  tại hai điểm phân biệt A; B  sao cho AB = $\sqrt{10}$

A. m= 2

B. m=3

C. m= 1

D. m= 4

Xem lời giải »

Câu 14:

Hàm số y = x⁸ + (x⁴ – 1) ² + 5  đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2]  lần lượt tại hai điểm có hoành độ x₁; x₂. Khi đó tích x₁.x₂  có giá trị bằng:

A. 1.

B. 2.

C. 3/2.

D. 0.

Xem lời giải »

Câu 15:

Cho phương trình $\sqrt{4x-1}+\sqrt{4x^2-1}$ =1 có nghiệm duy nhất có dạng b/a, trong đó a; b là số tự nhiên, b/a là  phân số tối giản. Hãy tính giá trị của  a+ 2b

A. 4

B. 5

C. 6

D.7

Xem lời giải »

Câu 16:

Cho phương trình x³ - 3x² + 1 - m = 0 (1). Điều kiện của tham số m  để (1) có ba nghiệm phân biệt thỏa x₁ < 1 < x₂ < x₃  khi

A. m = -1

B. -1 < m < 3

C. -3 < m < -1

D. Đáp án khác

Xem lời giải »

Câu 17:

Cho phương trình: $2x^3+x^2-3x+1=2\left(3x-1\right)\sqrt{3x-1}$

Tính tổng các nghiệm cùa phương trình là :

A.1

B.2

C.3

D.4

Xem lời giải »

Câu 18:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{1}{3}{x}^3-\frac{1}{2}m{x}^2+2mx-3m+4$ nghịch biến trên một đoạn có độ dài là  3?

A. m= -1; m= 9.

B. m= -1

C. m= 3.

D. Đáp án khác

Xem lời giải »

Câu 19:

Với giá trị nào của tham số m thì (C): y=x³-3(m+1) x²+2(m²+4m+1)x-4m(m+1) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?

A. $\frac{1}{2}<m\ne 1$

B. m> 1/ 2

C. m< 1/2

D. m

Xem lời giải »

Câu 20:

Cho hàm số  y=x³-3x²+4 có đồ thị (C) . Gọi d  là đường thẳng qua  I(1; 2) với hệ số góc k . Có bao nhiêu   giá trị nguyên của k  để d  cắt (C)  tại ba điểm phân biệt I, A, B sao cho I  là trung điểm của đoạn thẳng  AB là

A. 4

B. 1

C.  6

D. vô số

Xem lời giải »

Câu 1:

Cho hàm số y= x³-3x²-m-1 có đồ thị (C) . Giá trị của tham số m để đồ thị (C)  cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là

A.m=0

B. m=3

C. m=-3

D. $m=\pm 6$

Xem lời giải »

Câu 2:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{\tan x-2}{\tan x - m}$  đồng biến trên khoảng $\left(0;\frac{\mathrm{\pi }}{4}\right)$?

A. 1≤ m < 2.

B. m≤ 0 .

C. m> 2.

D. Cả A và B đúng

Xem lời giải »

Câu 3:

Tập nghiệm của bất phương trình:  $\sqrt{5x-1}+\sqrt{x+3}\ge 4$ có bao nhiêu giá trị nguyên trong ( 0; 2008]

A.2006 

B. 2001 

C. 2008 

D. 2007

Xem lời giải »

Câu 4:

Cho hàm số  có đồ thị (C) $y=\frac{2x+1}{x-1}$ và đường thẳng  d: y=x+m. Đường thẳng d cắt đồ thị (C)  tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là

A.m = 1

B.m = 1 hoặc m = - 5

C.m = 5

D.m = - 5

Xem lời giải »

Câu 5:

Bất phương trình  $\sqrt{2x^3+3x^2+6x+16}-\sqrt{4-x}\ge 2\sqrt{3}$  có tập nghiệm là [a; b]. Hỏi tổng a²+ b² có giá trị là bao nhiêu?

A. 4

B. 7

C. 10

D. 17

Xem lời giải »

Câu 6:

Bất phương trình   $\sqrt{x^2-2x+3}-\sqrt{x^2-6x+11}>\sqrt{3-x}-\sqrt{x-1}$ có tập nghiệm là ( a; b]. Hỏi 4a-b có giá trị là bao nhiêu?

A. 1.

B. 3.

C. 5.

D. 7

Xem lời giải »

Câu 7:

Cho hàm số: y = x³+2mx²+3(m-1)x+2  có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C)  tại ba điểm phân biệt A(0; -2); B và C. Với  M(3;1)  giá trị của tham số m để tam giác MBC  có diện tích bằng $2\sqrt{7}$  là

A. m=-1 

B. m=-1 hoặc m=4 

C. m=4 

D. Không tồn tại m

Xem lời giải »

Câu 8:

Phương trình $x^3+x(x+1)=m{(x^2+1)}^2$  có nghiệm thực khi và chỉ khi:

A. m< 3/4

B.  $\frac{-1}{4}\le m\le \frac{3}{4}$

C. m> 3

D. Đáp án khác

Xem lời giải »

Câu 9:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình $\sqrt{x^2-4x+5}=m+4x-x^2$  có đúng 2 nghiệm dương?

A. $-1\le m\le 3.$

B. $-3<m<\sqrt{5}$.

C. $-\sqrt{5}<m<3.$

D. $-3\le m\le 3.$

Xem lời giải »

Câu 10:

Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x²- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx² + (m + 1) x + m + 2≥0?

A. m< -1

B. $m\le -\frac{4}{7}$.

C. $m\ge -\frac{4}{7}$.

D. m> -1

Xem lời giải »

Câu 11:

Cho hàm số $y=\frac{1}{3}{x}^3-m{x}^2-x+m+\frac{2}{3}$  có đồ thị (C) . Tất cả các giá trị của tham số m  để (C)  cắt trục Ox tại ba điểm phân biệt có hoành độ x₁; x₂; x₃  thỏa ${x_1}^2+{x_2}^2+{x_3}^2>15$ là 

A. m>1 hoặc m<-1

B. m< -1

C. m>0

D. m>1

Xem lời giải »

Câu 12:

Tìm tất cả các giá trị thực của tham số m  sao cho phương trình $\sqrt{x^2+mx+2}=2x+1$  có hai nghiệm thực?

A. $m\le 3$

B. $m\le 5$

C. m>1

D. đáp án khác

Xem lời giải »

Câu 13:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình   $3\sqrt{x-1}+m\sqrt{x+1}=2\sqrt[4]{x^2-1}$ có hai nghiệm thực?

A. $\frac{1}{3}\le m<1.$

B. $-1\le m\le \frac{1}{4}.$

C. $-2\le m\le \frac{1}{3}.$

D. $0\le m\le \frac{1}{3}.$

Xem lời giải »

Câu 14:

Cho hàm số y= f(x)  xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x)  như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d)   .  Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x)  trên [ a; e]?

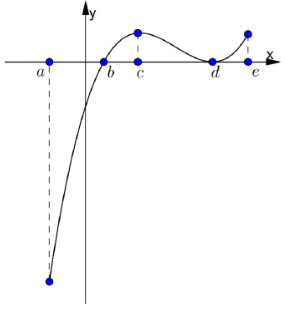
A. $\left\{\begin{array}{l}\underset{[a,e]}{max} f\left(x\right)=f\left(c\right)\\ \underset{[a,e]}{min} f\left(x\right)=f\left(a\right)\end{array}\right.$

B. $\left\{\begin{array}{l}\underset{[a,e]}{max} f\left(x\right)=f\left(a\right)\\ \underset{[a,e]}{min} f\left(x\right)=f\left(b\right)\end{array}\right.$

C. $\left\{\begin{array}{l}\underset{[a,e]}{max} f\left(x\right)=f\left(e\right)\\ \underset{[a,e]}{min} f\left(x\right)=f\left(b\right)\end{array}\right.$

D. $\left\{\begin{array}{l}\underset{[a,e]}{max} f\left(x\right)=f\left(d\right)\\ \underset{[a,e]}{min} f\left(x\right)=f\left(b\right)\end{array}\right.$

Xem lời giải »

Câu 15:

Cho hàm số y= f(x) = x⁴+ 2mx²+ m. Tìm m để f( x) >0 với mọi m.

A. m> 0

B. m< 0

C. m< 1

D. m> 1

Xem lời giải »

Câu 16:

Cho hàm số y= x⁴-(3m+4)x²+m² có đồ thị là (C).  Có mấy giá trị nguyên của m để đồ thị (C) cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng.

A: 0

B: 1

C: 2

D: 3

Xem lời giải »

Câu 17:

Tìm tất cả các giá trị thực của tham số  sao cho bất phương trình: $-x^3+3mx-2<-\frac{1}{x^3}$  nghiệm đúng mọi x≥ 1 ?

A. m< 1

B. m< 2/3

C. $m\ge \frac{3}{2}.$

D. $-\frac{1}{3}\le m\le \frac{3}{2}$

Xem lời giải »

Câu 18:

Tìm giá trị nguyên lớn nhất của m để: $\sqrt{x^2-2x-3}+\sqrt{8+2x-x^2}>m, (*)$ có nghiệm

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 19:

Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x³-3( m+1) x²+ 12mx-3m+ 4 ( C)  có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm  C(-1; -9/2) lập thành tam giác nhận gốc tọa độ  làm trọng tâm.

A. m= -1/2

B. m= -2

C. m=2

D. m =1/2

Xem lời giải »

Câu 20:

Cho hàm số y= x⁴- 2( 1-m²) x²+ m+1. Tồn tại giác trị của m  để  hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?

A. m là số nguyên dương

B. m không là số nguyên

C. m= 1

D. Tất cả sai

Xem lời giải »

Câu 1:

Cho hàm số $y=-x^3+3x^2-3x+1$, mệnh đề nào sau đây là đúng?

A. Hàm số luôn nghịch biến.

B. Hàm số luôn đồng biến

C. Hàm số đạt cực đại tại x = 1

D. Hàm số đạt cực tiểu tại x = 1

Xem lời giải »

Câu 2:

Hàm số: $f\left(x\right) = \cos x + \sin x \tan \frac{x}{2}$ là hàm hằng trên khoảng nào sau đây?

A. $\left(0;\mathrm{\pi }\right)$

B. $\left(\frac{\mathrm{\pi }}{3};2\right)$

C. R

D. $\left(-\frac{\mathrm{\pi }}{4};\frac{5\mathrm{\pi }}{4}\right)$

Xem lời giải »

Câu 3:

Cho hàm số $y=x^2-2\left|x\right|+2$ và các mệnh đề

(1) Hàm số trên liên tục trên R

(2) Hàm số trên có đạo hàm tại x = 0

(3) Hàm số trên đạt GTNN tại x = 0.

(4) Hàm số trên đạt GTLN tại x = 0.

(5) Hàm số trên là hàm chẵn

(6) Hàm số trên cắt trục hoành tại duy nhất một điểm

Trong các mệnh đề trên, số mệnh đề đúng là

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 4:

Cho hàm số $y=\frac{x+1}{1-x}$ và các mệnh đề sau

(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,

(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.

(3) Hàm số trên nhận y = -1 là tiệm cận đứng.

(4) Hàm số trên luôn đồng biến trên R. 

Trong số các mệnh đề trên, số mệnh đề sai là

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 5:

Trong các khẳng định sau về hàm số $y=-\frac{1}{4}{x}^4+\frac{1}{2}{x}^2-3$ khẳng định nào là đúng?

A. Hàm số có điểm cực tiểu là x = 0

B. Hàm số có hai điểm cực đại là x = ±1

C. Cả A và B đều đúng

D. Cả A và B đều sai

Xem lời giải »

Câu 6:

Trong các mệnh đề sau, hãy tìm mệnh đề sai:

A. Hàm số $y=-x^3+3x^2-3$ có cực đại và cực tiểu;

B. Hàm số $y=x^3+3x+1$ có cực trị;

C. Hàm số $y=-2x+1+\frac{1}{x+2}$ không có cực trị;

D. Hàm số $y=-2x+1+\frac{1}{x+2}$ nghịch biến trên từng khoảng xác định. 

Xem lời giải »

Câu 7:

Lưu lượng xe vào hầm cho bởi công thức $f\left(v\right)=\frac{290,4v}{0,36v^2+13,2v+264}$ trong đó v (km/h) là vận tốc trung bình của các xe khi vào hầm. Với giá trị xấp xỉ nào của v thì lưu lượng xe là lớn nhất?

A. 26

B. 27

C. 28

D. 29

Xem lời giải »

Câu 8:

Đồ thị hàm số nào sau đây có hình dạng như hình bên?

A. $y=x^3+3x+1$

B. $y=x^3-3x+1$

C. $y=-x^3-3x+1$

D. $y=-x^3+3x+1$

Xem lời giải »

Câu 9:

Số đường tiệm cận của đồ thị hàm số $y=\frac{3x+1}{x^2-4}$ là 

A. 3

B. 2

C. 1

D. 4

Xem lời giải »

Câu 10:

Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2${\sin }^{2}x$ - cosx + 1 thì M.m bằng

A. 0

B. $\frac{25}{8}$

C. $\frac{25}{4}$

D. 2

Xem lời giải »

Câu 11:

Hàm số nào sau đây là hàm số đồng biến trên R

A. $y=(x^2-1{)}^2-3x+2$

B. $y=\frac{x}{\sqrt{x^2+1}}$

C. $y=\frac{x}{x+1}$

D. y = tanx

Xem lời giải »

Câu 12:

Cho hàm số $y=-x^2-4x+3$ có đồ thị (C). Nếu tiếp tuyến tại M của (C) có hệ số góc bằng 8 thì hoành độ điểm M là:

A. 12

B. -6

C. -1

D. 5

Xem lời giải »

Câu 13:

Cho hàm số $y=-x^4+2x^2-1$. Số giao điểm của đồ thị hàm số với trục Ox là

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 14:

Cho hàm số y = 3sinx - 4${\sin }^{3}x$. Giá trị lớn nhất của hàm số trên khoảng $\left(-\frac{\pi }{2} ; \frac{\mathrm{\pi }}{2}\right)$ bằng

A. -1

B. $\frac{\mathrm{\pi }}{6}$

C. 1

D. $-\frac{\mathrm{\pi }}{6}$

Xem lời giải »

Câu 15:

Cho hàm số $y=x^3-3x^2+1.$ Tích các giá trị cực đại và giá trị cực tiểu của hàm số bằng

A. -6

B. -3

C. 0

D. 3

Xem lời giải »

Câu 16:

Số đường thẳng đi qua điểm A(0; 3) và tiếp xúc với đồ thị hàm số $y=x^4-2x^2+3$ là

A. 0

B. 1

C. 2

D. 3

Xem lời giải »

Câu 17:

Thể tích V của 1kg nước ở nhiệt độ $T(0° \le T \le 30°)$ được cho bởi công thức V = 999,87 - 0,06426T + 0,0085043$T^2$ - 0,0000679$T^3$. Ở nhiệt độ xấp xỉ bao nhiêu thì nước có khối lượng riêng lớn nhất?

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 18:

Hàm số $y = \frac{-2mx +m}{x-1}$ đồng biến trên từng khoảng xác định của nó khi

A. m > 0    

B. m < 0  

C. m ≠ 1    

D. m = 0

Xem lời giải »

Câu 19:

Trong các tiếp tuyến tại các điểm trên đồ thị hàm số $y=x^3-3x^2+2,$ tiếp tuyến có hệ số góc nhỏ nhất bằng:

A. -3

B. 3

C. -4

D. 0  

Xem lời giải »

Câu 20:

Hàm số nào sau đây có bảng biến thiên như hình bên?

A. $y = \frac{2x-1}{x-2}$

B. $y = \frac{2x-5}{x-2}$

C. $y=\frac{x+3}{x+2}$

D. $y=\frac{2x+3}{x+2}$

Xem lời giải »

Câu 21:

Hàm số $y=x^3-3x^2+mx$ đạt cực tiểu tại x = 2 khi:

A.m < 0   

B. m > 0   

C. m = 0    

D. m ≠ 0

Xem lời giải »

Câu 22:

Hàm số $y=\frac{1}{3}{x}^3+(m+1)x^2-(m+1)x+1$ đồng biến trên tập xác định của nó khi:

A. -2 ≤ m ≤ -1    

B. -2 < m < -1   

C. m < -2   

D. m > -1

Xem lời giải »

Câu 23:

Cho đồ thị hàm số $y=x^3-2x^2+2x$ (C). Gọi $x_1,x_2$ là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng $y = -x + 2017$. Khi đó $\left(x_1+x_2\right)$ bằng

A. 4

B. $-\frac{4}{3}$

C. $\frac{4}{3}$

D. -1

Xem lời giải »

Câu 24:

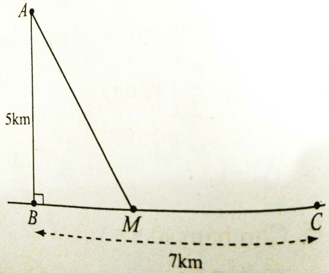
Một ngọn hải đăng đặt trại vị trí A cách bờbiển một khoảng AB = 5km. Trên bờ biển có một kho vị trí C cách B một khoảng là 7km. Do địa hình hiểm trở, người canh hải đăng chỉ có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C, với vận tốc 6km/h. Vậy vị trí M cách B một khoảng bao xa thì người đó đến kho là nhanh nhất?

A. 3,5km   

B. 4,5km   

C. 5,5km   

D. 6,5km

Xem lời giải »

Câu 1:

Cho hàm số $y=f\left(x\right)$ có $\underset{x\to +\infty }{\lim }f\left(x\right)=0$ và $\underset{x\to -\infty }{\lim }f\left(x\right)=+\infty$. Mệnh đề nào sau đây là đúng?

A. Đồ thị hàm số  = f(x) không có tiệm cận ngang

B. Đồ thị hàm số y = f(x) có một tiệm cận đứng là đường thẳng y = 0

C. Đồ thị hàm số y = f(x) có tiệm cận ngang là trục hoành

D. Đồ thị hàm số y = f(x) nằm phía trên trục hoành

Xem lời giải »

Câu 2:

Hỏi a và b thỏa mãn điều kiện nào để hàm số $y=a{x}^4+b{x}^2+c\left(a\ne 0\right)$ có đồ thị dạng như hình bên?

A. a > 0 và b > 0

B. a > 0 và b < 0

C. a < 0 và b > 0

D. a < 0 và b < 0

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như hình bên. Số đường tiệm cận ngang của đồ thị hàm số y = f(x) là:

A. 0

B. 2

C. 3

D. 1

Xem lời giải »

Câu 4:

Hàm số nào dưới đây có tập xác định bằng R?

A. $y=\frac{1}{2x}$

B. $y=\frac{2x-1}{x+1}$

C. $y=\sqrt{x^2+1}$

D. $y=\frac{x-1}{x^2-1}$

Xem lời giải »

Câu 5:

Số cực trị của hàm số $y=\frac{ax+b}{cx+d}$ là:

A. 0

B. 1

C. 2

D. 3

Xem lời giải »

Câu 6:

Tiệm cận đứng của đồ thị hàm số $y=\frac{ax+b}{cx+d}$ với $ad-bc\ne 0$ là:

A. $x=-\frac{d}{c}$

B. $y=-\frac{d}{c}$

C. $y=\frac{c}{a}$

D. $x=\frac{a}{c}$

Xem lời giải »

Câu 7:

Giao điểm hai đường tiệm cận của đồ thị hàm số $y=\frac{-x+1}{2x-3}$ là:

A. $\left(\frac{1}{2};\frac{3}{2}\right)$

B. $\left(-\frac{3}{2};\frac{1}{2}\right)$

C. $\left(\frac{3}{2};-\frac{1}{2}\right)$

D. $\left(-\frac{1}{2};\frac{3}{2}\right)$

Xem lời giải »

Câu 8:

Cho hàm số y = f(x) có bảng biến thiên:

Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?

A. $y=\frac{3x-2}{2x+3}$

B. $y=\frac{x+2}{2x+3}$