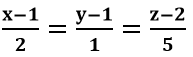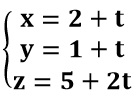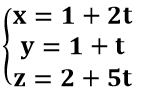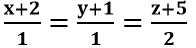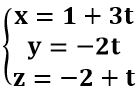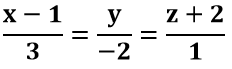Các dạng bài tập Phương trình đường thẳng trong không gian chọn lọc, có đáp án - Toán lớp 12
Các dạng bài tập Phương trình đường thẳng trong không gian chọn lọc, có đáp án
Với Các dạng bài tập Phương trình đường thẳng trong không gian chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình đường thẳng trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
- Các công thức về đường thẳng, phương trình đường thẳng trong không gian Xem chi tiết
- 19 dạng bài tập Viết phương trình đường thẳng trong đề thi Đại học có lời giải Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và có vecto chỉ phương u Xem chi tiết
- Viết phương trình đường thẳng đi qua 2 điểm Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và vuông góc với mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và song song với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng là giao tuyến của hai mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, song song với mặt phẳng và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng nằm trong mặt phẳng, đi qua 1 điểm và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, cắt đường thẳng d và song song với mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và vuông góc với 2 đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và cắt hai đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, vuông góc với đường thẳng d1 và cắt đường thẳng d2 Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, cắt và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng nằm trong mặt phẳng và cắt hai đường thẳng Xem chi tiết
- Viết phương trình đường thẳng song song với đường thẳng và cắt 2 đường thẳng Xem chi tiết
- Viết phương trình đường vuông góc chung của hai đường thẳng chéo nhau Xem chi tiết
- Viết phương trình đường thẳng là hình chiếu của đường thẳng lên mặt phẳng Xem chi tiết
- Vị trí tương đối của hai đường thẳng trong không gian Xem chi tiết
- Vị trí tương đối của đường thẳng và mặt phẳng Xem chi tiết
- Vị trí tương đối của đường thẳng và mặt cầu Xem chi tiết
- Hình chiếu của một điểm lên đường thẳng, mặt phẳng Xem chi tiết
- Khoảng cách từ 1 điểm đến 1 đường thẳng; Khoảng cách giữa 2 đường thẳng chéo nhau Xem chi tiết
- Viết phương trình đường thẳng liên quan đến khoảng cách Xem chi tiết
- Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng Xem chi tiết
- Tìm điểm thuộc đường thẳng thỏa điều kiện cho trước, bài toán về cực trị,... Xem chi tiết
- 60 câu hỏi trắc nghiệm đường thẳng trong không gian có lời giải Xem chi tiết
Viết phương trình đường thẳng đi qua 1 điểm và có vecto chỉ phương u
A. Phương pháp giải
Nếu đường thẳng d đi qua điểm M(x0; y0; z0) và vecto chỉ phương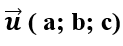 
thì
+ Phương trình tham số của đường thẳng d: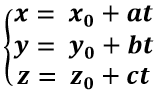 
+ Phương trình chính tắc của đường thẳng d ( với a.b.c ≠ 0) là:
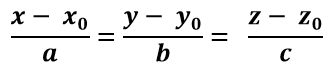
Như vậy để xác định được phương trình đường thẳng d ta cần xác định được một điểm thuộc đường thẳng và vecto chỉ phương của đường thẳng đó
B. Ví dụ minh họa
Ví dụ 1: Cho đường thẳng Δ biết Δ đi qua A (2 ; 1 ; 5) và có vectơ chỉ phương u→ =(1;1;2). Tìm mệnh đề đúng
A. Phương trình chính tắc của đường thẳng d: 
B. Phương trình tham số của đường thẳng d: 
C. Phương trình tham số của đường thẳng d: 
D. Phương trình chính tắc của đường thẳng d: 
Phương trình tham số của đường thẳng Δ là:
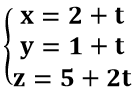
Trong đó t là tham số
Phương trình chính tắc của đường thẳng Δ là:
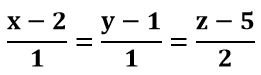
Chọn B.
Ví dụ 2: Cho đường thẳng d có phương trình tham số: 
Tìm mệnh đề sai ?
A. Đường thằng d đi qua điểm A( 4; - 2; - 1) .
B. Đường thẳng d nhận vecto u→ ( - 6; 4; -2) làm vecto chỉ phương
C. Đường thẳng d có phương trình chính tắc là: 
D. Đường thẳng d có vecto pháp tuyến là: n→ ( 3; -2; 1)
Hướng dẫn giải
+ Từ phương trình tham số => d đi qua điểm M (1; 0; -2) và vectơ chỉ phương
u→ =(3;-2;1)Phương trình chính tắc của đường thẳng d là:
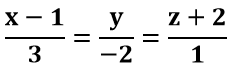
+ Cho t= 1 ta được điểm A( 4; -2; -1) thuộc đường thẳng d.
+ Do hai vecto u→ =(3;-2;1) và u'→ ⃗=( -6;4;-2) cùng phương mà vecto u→ =(3;-2;1) là vecto chỉ phương của đường thẳng d nên vecto u'→ =( -6;4;-2) cũng là vecto chỉ phương của đường thẳng d.
=> A; B; C đúng và D sai
Chọn D.
Ví dụ 3: Cho đường thẳng d có phương trình chính tắc: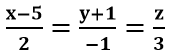 
Tìm mệnh đề sai?
A. Đường thẳng d đi qua A( -5; 1; 0)
B. Đường thẳng d có vecto chỉ phương u→ ( 2; -1; 3)
C. Phương trình tham số của đường thẳng d: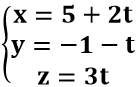 
D. Đường thẳng d đi qua điểm H( 9; - 3; 6)
Hướng dẫn giải
Từ phương trình chính tắc => d đi qua điểm M (5; -1; 0) và vectơ chỉ phương u→ =(2;-1;3)
=> Phương trình tham số của của đường thẳng d là: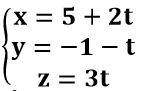 
+ Cho t= 2 ta được điểm H( 9; - 3; 6) thuộc đường thẳng d.
=> B; C và D d đúng ; A sai
Chọn A .
Cách viết phương trình đường thẳng đi qua 2 điểm
A. Phương pháp giải
+ Tính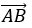 
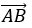
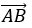
, đường thẳng d nhận vecto
làm vecto chỉ phương ( có thể chọn một vecto cùng phương với
làm vecto chỉ phương.
+ Đường thẳng d đi qua A và nhận vecto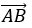
làm vecto chỉ phương
=> phương trình tham số và phương trình chính tắc của đường thẳng d
B. Ví dụ minh họa
Ví dụ 1: Trong không gian với hệ tọa độ Oxyz; cho đường thẳng Δ đi qua A (1; 1; 3) và B (2; 0; 5). Tìm mệnh đề sai?
A. phương trình tham số của Δ là: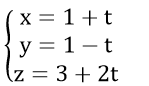 
B. Phương trình chính tắc của Δ là: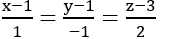 
C. Đường thẳng Δ đi qua điểm H( 0; 2; 1)
D. Đường thẳng Δ đi qua điểm K( - 4; - 6; - 7)
Hướng dẫn giải
Ta có: 
Δ đi qua A và B nên vectơ chỉ phương của Δ là u→
=
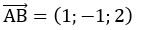
Vậy phương trình tham số của Δ là: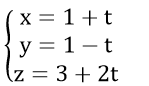
Phương trình chính tắc của Δ là: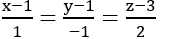
Cho t= - 1 ta được điểm H( 0;2; 1) thuộc đường thẳng Δ.
Cho t= -5 ta được điểm M( - 4; 6; - 7) thuộc đường thẳng Δ
Chọn D.
Ví dụ 2: Cho tam giác ABC có A(1; -2; 5), B(3; -1; 4), C(4; 1; -3). Chọn mệnh đề sai về phương trình đường trung tuyến AM
A. phương trình tham số của AM là: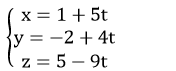 
B. Phương trình chính tắc của AM là: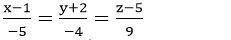 
C. Phương trình tham số của AM là: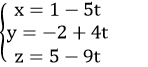
D. Phương trình chính tắc của AM là: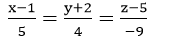
Hướng dẫn giải
Trung điểm M của BC là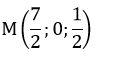
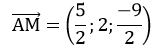
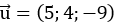
=>vectơ chỉ phương của AM là 
Vậy phương trình tham số của AM là: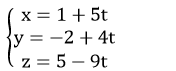
Phương trình chính tắc của AM là:
Do vecto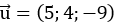
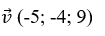
là vecto chỉ phương của đường thẳng AM nên vecto 
cũng là vecto chỉ phương của đường thẳng AM.
=> Đường thẳng AM cũng có phương trình chính tắc là: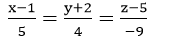
Chọn C.
Ví dụ 3:Viết phương trình chính tắc của đường thẳng Δ biết Δ đi qua A (2; 1; 3) và B (1; -2; 1)?
A.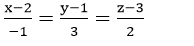
B.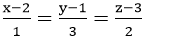
C.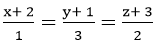
D.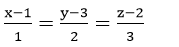
Hướng dẫn giải
Vì đường thẳng Δđi qua 2 điểm A (2; 1; 3) và B (1; -2; 1) nên có véc tơ chỉ phương là u→=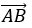
=(1;3;2)
Đồng thời đường thẳng Δ đi qua điểm A (2; 1; 3) nên có phương trình là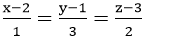
Chọn B.
Viết phương trình đường thẳng đi qua 1 điểm và vuông góc với mặt phẳng
A. Phương pháp giải
+ Tìm vecto pháp tuyến của mặt phẳng (α) .
+ Vectơ chỉ phương của đường thẳng d cùng phương với vectơ pháp tuyến của mặt phẳng (α) vì d ⊥ (α)
+ Áp dụng cách viết phương trình đường thẳng đi qua một điểm biết vecto chỉ phương của đường thẳng đó.
Chú ý: Các trường hợp đặc biệt.
+ Nếu Δ vuông góc với mặt phẳng (Oxy) thì có VTCP là uΔ→ = k→ = (0;0;1) .
+ Nếu Δ vuông góc với mặt phẳng (Oxz) thì có VTCP là uΔ→ = j→ =(0;1;0) .
+Nếu Δvuông góc với mặt phẳng (Oyz) thì có VTCP là uΔ→ = i→ =(1;0;0) .
B. Ví dụ minh họa
Ví dụ 1:Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng Δ đi qua A(1;0; -1) và vuông góc với mặt phẳng (P): 2x - y + z + 9 = 0. Tìm mệnh đề đúng?
A. Vậy phương trình tham số của Δ là: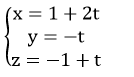
B. Phương trình chính tắc của Δ là: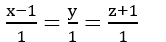
C. Vậy phương trình tham số của Δ là: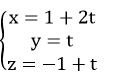
D. Phương trình chính tắc của Δ là: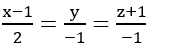
Hướng dẫn giải
Vì đường thẳng Δ vuông góc với mặt phẳng (α) nên vectơ chỉ phương của Δ là:
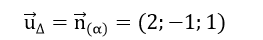
Vậy phương trình tham số của Δ là: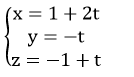
Phương trình chính tắc của Δ là:
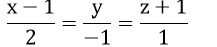
Chọn A.
Ví dụ 2:Trong không gian với hệ trục tọa độ Oxyz; cho đường thẳng d đi qua M (1; 3; -2) và vuông góc với mặt phẳng (Oxy). Tìm mệnh đề sai?
A. phương trình tham số của Δ là: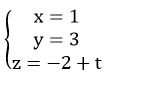
B. Đường thẳng d không có phương trình chính tắc.
C. Điểm H( 1;3; 4) thuộc đường thẳng d
D. Đường thẳng d vuông góc với mặt phẳng ( P): 2x+ 3y+ z= 0.
Hướng dẫn giải
Mặt phẳng (Oxy) có phương trình z= 0 nên có vecto pháp tuyến là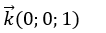 
Vì đường thẳng d vuông góc với mặt phẳng (Oxy) nên vectơ chỉ phương của d là:
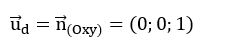
Vậy phương trình tham số của Δ là: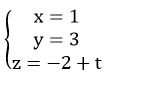
và đường thẳng d không có phương trình chính tắc
Cho t= 6 ta được điểm H( 1;3; 4) thuộc đường thẳng d.
Mặt phẳng (P): 2x+ 3y + z= 0 có vecto pháp tuyến là :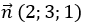 
Ta có: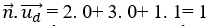 
=> Đường thẳng d và mặt phẳng ( P) không vuông góc với nhau.
Chọn D.
