Các dạng bài tập Dạng đại số của số phức chọn lọc, có đáp án - Toán lớp 12
Các dạng bài tập Dạng đại số của số phức chọn lọc, có đáp án
Với Các dạng bài tập Dạng đại số của số phức chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đại số của số phức từ đó đạt điểm cao trong bài thi môn Toán lớp 12.
- 6 dạng bài tập số phức cơ bản trong đề thi Đại học có lời giải Xem chi tiết
- Dạng 1: Cộng trừ số phức Xem chi tiết
- Dạng 2: Nhân chia số phức Xem chi tiết
- Dạng 3: Tìm số phức liên hợp Xem chi tiết
- Dạng 4: Tìm môđun của số phức Xem chi tiết
- 26 bài tập trắc nghiệm Số phức cơ bản chọn lọc, có đáp án Xem chi tiết
Bài tập cộng trừ số phức
Phương pháp giải
Cho hai số phức z1 = a + bi và z2 = c + d.i thì:
Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
Phép trừ số phức: z1 - z2 = (a - c) + (b - d)i
Ví dụ minh họa
Ví dụ 1:Ví dụ 1: Cho hai số phức z1 = 3 - 2i; z2 = 1 + 3i. Tìm số phức z = z1 + z2.
A. 4 + i B. 9 - i C.-1 + 10i D. 4 + 3i
Hướng dẫn:
Ta có; z = z1 + z2 = (3 - 2i) + (1 + 3i) = (3 + 1)+(-2 + 3)i = 4 + i
Chọn A.
Ví dụ 2:Cho số phức z = a + bi và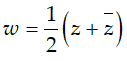 
. Mệnh đề sau đây là đúng?
A. w là một số thực B .w = 2
C. w là một số thuần ảo. D.w = i
Hướng dẫn:
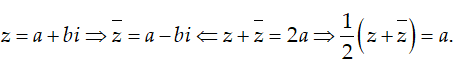
Chọn A.
Ví dụ 3:Cho hai số phức z1 = 2 - 3i; z2 = 1 + i số phức z = z1 – z2.
A. z = 3 + 3i B. z = 1 - 4i. C. z = 2 - 3i. D. z = 3 - i.
Hướng dẫn:
Ta có z = z1 – z2. = (2 -3i) - (1 + i) = (2 - 1) + (-3 - 1)i = 1 - 4i
Chọn B.
Ví dụ 4: Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a ; b ; a’; b’ để z + z’ là một số thuần ảo.
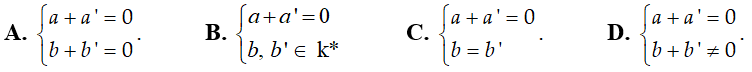
Hướng dẫn:
Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo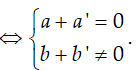 
Chọn D.
Bài tập nhân chia số phức
Phương pháp giải
Phép nhân số phức: z1.z2 = (ac - bd) + (ad + bc).i
Phép chia số phức:
Số phức nghịch đảo của z = a + bi ≠ 0 là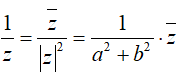 
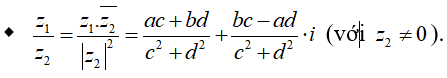
Ví dụ minh họa
Ví dụ 1:Cho hai số phức z = i. Tìm số phức w = z5.
A. w = i B. w = -1. C. w = 1 D. w = -i.
Hướng dẫn:
Ta có w = z5 = i5 = i4.i = 1.i = i
Chọn A.
Ví dụ 2: Cho hai số phức z1 = i; z2 = 1 + 2i Tìm số phức z = z1.z2.
A. z = 1 B. z = 2 + i C. z = -1 + i. D. z = -2 + i
Hướng dẫn:
Ta có z = z1.z2 = i.(1 + 2i) = i + 2i2 = i - 2
Chọn D.
Ví dụ 3: Cho 2 số phức z1 = 1 - i ; z2 = 1 + i .Tìm phần ảo của số phức w = z1.z2
A. -2 B. -1 C. 0 D. 1
Hướng dẫn:
Ta có w = (1 - i)(1 + i) = 12 – i2 = 1 + 1 = 2.
Vậy phần ảo của số phức w là 0.
Chọn C.
Cách tìm số phức liên hợp
Phương pháp giải
Cho số phức z = a + bi. Ta gọi số phức liên hợp của z là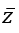 
= a - bi.
Kết quả: ∀ z ∈ C ta có:
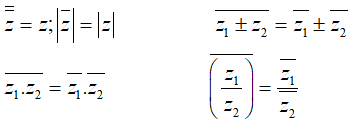
Z là số thực khi z =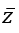
Z là số thuần ảo khi z = -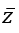
Ví dụ minh họa
Ví dụ 1: Cho số phức z = 1 + 3i Tìm số phức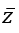
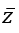
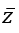
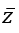
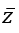
A. = 1 - 3i. B. = 3 - i. C. = 3 + i. D. = 1 + 3i.
Hướng dẫn:
Với z = 1 + 3i thì 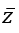= 1 - 3i
Chọn A.
Ví dụ 2: Cho số phức z = -2 - 5i Tìm phần thực a và phần ảo b của số phức .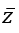
A. a = -2 ; b = 5 B. a = -2; b = -5 C. a = -5; b = 2 D. a = -5; b = -2
Hướng dẫn:
z = a + bi => 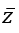= a - bi
Nên 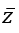= -2 + 5i vậy. Phần thực bằng a = -2 và phần ảo b = 5
Chọn A.
Ví dụ 3:Tìm số phức liên hợp của số phức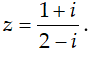 
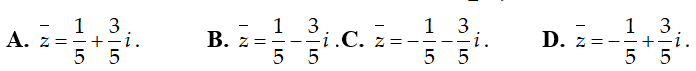
Hướng dẫn:
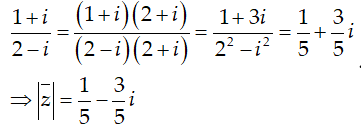
Chọn B.
Cách tìm môđun của số phức
Phương pháp giải
được gọi là môđun của số phức z.
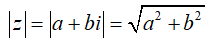
+) Kết quả: ∀z ∈ C ta có:
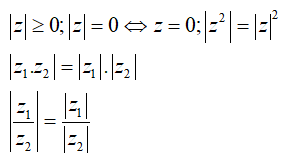
Ví dụ minh họa
Ví dụ 1:Tìm các số phức z thỏa mãn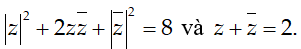 
A. z1 = -1 + i; z2 = 1 - i B. z1 = 1 + i; z2 = -1 - i
C. z1 = -1 + i ; z2 = -1 - i D. z1 = 1 + i; z2 = 1 - i
Hướng dẫn:
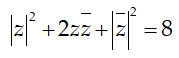
4(x2 + y2 ) = 8 → x2 + y2 = 2
Do đó x = 1 và y = ±1
Chọn D.
Ví dụ 2:: Cho số phức z = 2 - 3i. Tính |z|
A. |z| = 2. B. |z| = -3. C. |z| = √13. D. |z| = 13 .
Hướng dẫn:
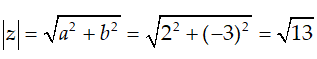
Chọn C
Ví dụ 3:Cho hai số phức z1 = 1 + 3i ; z2 = 2 - i Tính P = |z1 + z2|
A. P = √5 . B. P = 5 C. P = √10 D. P = √13
Hướng dẫn:
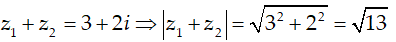
Chọn D.
