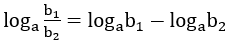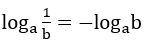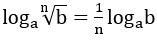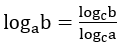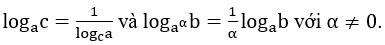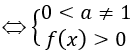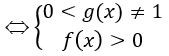Các dạng bài tập Hàm số mũ, lũy thừa, lôgarit chọn lọc - Toán lớp 12

---

Các dạng bài tập Hàm số mũ, lũy thừa, lôgarit chọn lọc

Với Các dạng bài tập Hàm số mũ, lũy thừa, lôgarit chọn lọc Toán lớp 12 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hàm số mũ, lũy thừa, lôgarit từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

• Lý thuyết hàm số mũ, hàm số logarit, hàm số lũy thừa chi tiết Xem chi tiết
• 4 Dạng bài tập Lũy thừa trong đề thi Đại học có lời giải Xem chi tiết
• 6 dạng bài tập Logarit trong đề thi Đại học có lời giải Xem chi tiết
• 4 dạng bài tập Hàm số mũ, hàm số logarit trong đề thi Đại học có lời giải Xem chi tiết
• 2 dạng bài tập Hàm số lũy thừa trong đề thi Đại học có lời giải Xem chi tiết
• Tìm điều kiện xác định của lũy thừa hay nhất Xem chi tiết
• Dạng bài tập Rút gọn biểu thức chứa lũy thừa cực hay Xem chi tiết
• Dạng bài tập về so sánh các lũy thừa cực hay Xem chi tiết
• Dạng bài tập Tính giá trị của biểu thức lũy thừa cực hay Xem chi tiết
• Dạng 1: Lũy thừa: lý thuyết, tính chất, phương pháp giải Xem chi tiết
• Trắc nghiệm lũy thừa Xem chi tiết
• Dạng 2: Lôgarit: lý thuyết, tính chất, phương pháp giải Xem chi tiết
• Trắc nghiệm Lôgarit Xem chi tiết
• Tìm điều kiện để biểu thức logarit xác định hay nhất Xem chi tiết
• Dạng bài tập Tính giá trị của biểu thức logarit cực hay Xem chi tiết
• Dạng bài tập Rút gọn biểu thức chứa logarit cực hay Xem chi tiết
• Dạng bài tập biểu diễn logarit này theo logarit khác cực hay Xem chi tiết
• Cách biến đổi đẳng thức đã cho thành đẳng thức logarit cực hay Xem chi tiết
• Cách so sánh biểu thức chứa logarit cực hay Xem chi tiết
• Dạng 3: Tìm tập xác định của hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Trắc nghiệm tìm tập xác định của hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Dạng 4: Các dạng bài tập về hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Trắc nghiệm về hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Dạng 5: Giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Trắc nghiệm giới hạn, đạo hàm của hàm số mũ, lũy thừa, lôgarit Xem chi tiết
• Tìm giá trị lớn nhất, nhỏ nhất của hàm số mũ, logarit, lũy thừa Xem chi tiết
• Viết phương trình tiếp tuyến của hàm số mũ, logarit, lũy thừa Xem chi tiết

Bài tập trắc nghiệm

• 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (cơ bản) Xem chi tiết
• 200 bài tập trắc nghiệm Hàm số mũ, lũy thừa, Lôgarit có lời giải (nâng cao) Xem chi tiết

Cách giải bài tập về Lũy thừa

A. Phương pháp giải & Ví dụ

    • Cho số thực b và số nguyên dương n (n ≥ 2). Số a được gọi là căn bậc n của số b nếu aⁿ = b.

    • Chú ý:

Số mũ α	Cơ số a	Lũy thừa aα
α = n ∈ N*	a ∈ R	aα = an = a⋅a⋯a (n thừa số a)
α = 0	a ≠ 0	aα = a0 = 1
α = -n, (n ∈ N*)	a ≠ 0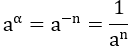
α = m/n,(m ∈ Z, n ∈ N*)	a > 0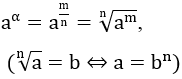
α = limrn, (rn ∈ Q,n ∈ N*)	a > 0	aα = limarn

2. Một số tính chất của lũy thừa

    • Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:

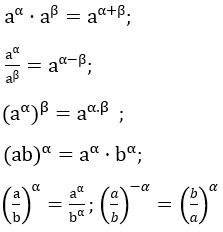
    • Nếu a > 1 thì a^α > a^β ⇔ α > β; Nếu 0 < a < 1 thì a^α > a^β ⇔ α < β.

    • Với mọi 0 > a < b, ta có: a^m < b^m ⇔ m > 0; a^m > b^m ⇔ m < 0

    • Chú ý:

        ◦ Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.

        ◦ Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

        ◦ Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

3. Một số tính chất của căn bậc n

    • Với a,b ∈ R;n ∈ N*, ta có:

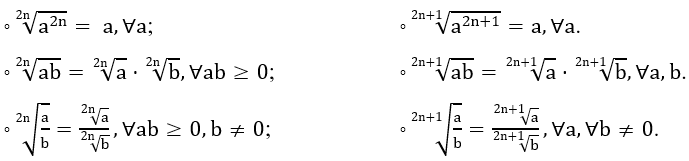
    • Với a,b ∈ R, ta có:

Ví dụ minh họa

Bài 1: Tính giá trị của biểu thức

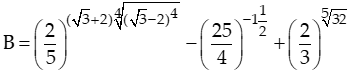
Hướng dẫn:

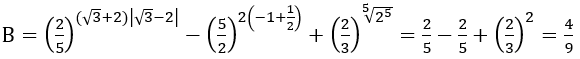
Bài 2: Biết 4^x + 4^-x = 23 tính giá trị của biểu thức P = 2^x + 2^-x :

Hướng dẫn:

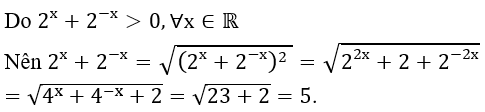
Bài 3: Cho các số thực dương a và b. Thu gọn biểu thức

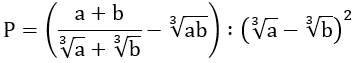
Hướng dẫn:

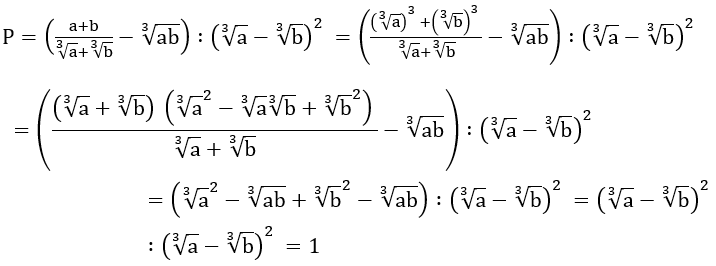
Cách giải bài tập về Lôgarit

A. Phương pháp giải & Ví dụ

1. Định nghĩa:

Cho hai số dương a,b với a ≠ 1. Số α thỏa mãn đẳng thức a^α = b được gọi là lôgarit cơ số a của b và kí hiệu là log_ab . Ta viết: α = log_ab ⇔ a^α = b.

2. Các tính chất: Cho a, b > 0, a ≠ 1, ta có:

    • log_aa = 1, log_a1 = 0

    • a^log_ab = b, log_a(a^α) = α

3. Lôgarit của một tích: Cho 3 số dương a, b₁, b₂ với a ≠ 1, ta có

    • log_a(b₁.b₂) = log_ab₁ + log_ab₂

4. Lôgarit của một thương: Cho 3 số dương a,b₁, b₂ với a ≠ 1, ta có

    •

    • Đặc biệt : với a, b > 0, a ≠ 1 ⇒

5. Lôgarit của lũy thừa: Cho a,b > 0, a ≠ 1, với mọi α, ta có

    • log_ab^α = αlog_ab

    • Đặc biệt:

6. Công thức đổi cơ số: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1, ta có

    •

    • Đặc biệt :

    Lôgarit thập phân và Lôgarit tự nhiên

        ♦ Lôgarit thập phân là lôgarit cơ số 10. Viết : log₁₀b = logb = lgb

        ♦ Lôgarit tự nhiên là lôgarit cơ số e. Viết : log_eb = lnb

Ví dụ minh họa

Bài 1: Rút gọn biểu thức B

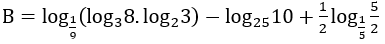
Hướng dẫn:

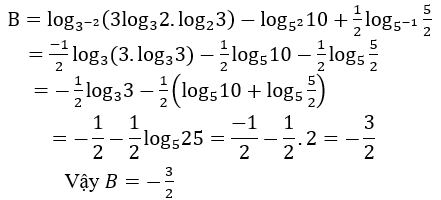
Bài 2: Tính giá trị của biểu thức P (với 0 < a ≠ 1; 0 < b ≠ 1).

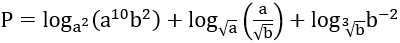
Hướng dẫn:

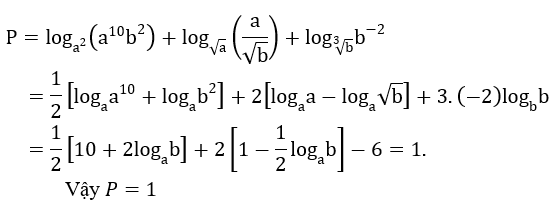
Bài 3: Tính log₂₄15 theo a, b , biết log₂5 = a, log₅3 = b.

Hướng dẫn:

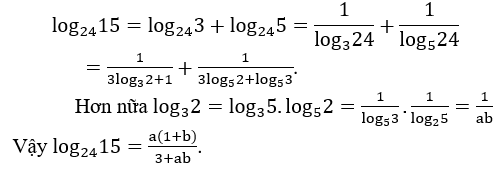
Tìm tập xác định của hàm số mũ, lũy thừa, lôgarit

A. Phương pháp giải & Ví dụ

Bài toán 1: Tập xác định của hàm lũy thừa, hàm vô tỷ

Xét hàm số y = [f(x)]^α

    • Khi α nguyên dương: hàm số xác định khi và chỉ khi f(x) xác định.

    • Khi α nguyên âm: hàm số xác định khi và chỉ khi f(x) ≠ 0.

    • Khi α không nguyên: hàm số xác định khi và chỉ khi f(x) > 0.

Bài toán 2: Tập xác định của hàm số logarit

    • Hàm số y = log_af(x) xác định

    • Hàm số y = log_g(x)f(x) xác định

    • Hàm số y = (f(x))^g(x) xác định ⇔ f(x) > 0

Ví dụ minh họa

Bài 1: Tìm tập xác định của hàm số

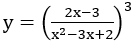
Hướng dẫn:

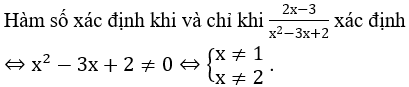
Bài 2: Tìm tập xác định D của hàm số y=(x²-1)^-8

Hướng dẫn:

Hàm số xác định khi và chỉ khi x²-1 ≠ 0 ⇔ x ≠ ±1

Bài 3: Tìm tập xác định của hàm số

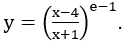
Hướng dẫn:

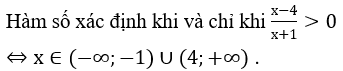
Bài 4: Tìm tập xác định D của hàm số y=log(x²-6x+5)

Hướng dẫn:

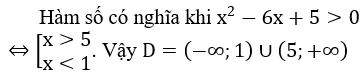
Bài 5: Tìm tập xác định của hàm số y=(x²-16)^-5-ln(24-5x-x²).

Hướng dẫn:

Tập xác định của hàm số y = (x²-16)^-5 - ln(24-5x-x²)là:

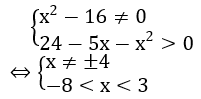
Vậy tập xác định là : D=(-8;3)\{-4}.