Bài tập ôn tập chương IV (mới nhất)
Haylamdo biên soạn và sưu tầm 50 bài tập Bài tập ôn tập chương IV Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Bài tập ôn tập chương IV
Câu 1:
Cho hai số phức z1 = 3i - 2; z2 = 5 + 3i. Tìm số phức z = z1 + z2.
A. 3 + 6i
B. 9 - i
C. -1 + 10i
D. 4 + 3i
Câu 2:
Cho số phức z = a + bi và . Mệnh đề sau đây là đúng?
A. w là một số thực
B . w = 2
C. w là một số thuần ảo.
D. w = i
Câu 3:
Cho hai số phức z1 = 2 - 3i; z2 = 4i - 10. Tìm số phức z = z1 – z2.
A. z = 3 + 3i.
B. z = 12 - 7i.
C. z = 2 - 3i.
D. z = 3 - i.
Câu 4:
Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
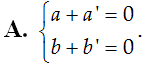
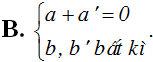
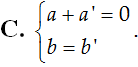
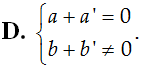
Câu 5:
Tìm số phức z thỏa mãn 3z - 3i = 6 - 9i
A. z = -1 + 2i
B. z = -3 + 2i
C. z = 1+ i
D. z = 2 - 2i
Câu 6:
Cho số phức z = 10i - 8. Tìm phần thực, phần ảo của số phức w = z - i
A. Phần thực bằng -8 và phần ảo bằng -8i
B. Phần thực bằng -2 và phần ảo bằng -3
C. Phần thực bằng 8 và phần ảo bằng 10i
D. Phần thực bằng – 8 và phần ảo bằng 9
Câu 7:
Cho hai số phức z1 = 3i - 4; z2 = 3 - i. Tìm số phức z = z1 – z2.
A. 6 - 5i
B. 7 + 4i
C. 4 + 4i
D. -7 + 4i
Câu 8:
Cho hai số phức z = i. Tìm số phức w = z5.
A. w = i.
B. w = -1.
C. w = 1.
D. w = -i.
Câu 9:
Cho hai số phức z1 = 1 + i; z2 = 1 - 2i. Tìm số phức z = z1.z2.
A. z = 1.
B. z = 3 - i.
C. z = -1 + i.
D. z = -2 + i.
Câu 10:
Cho 2 số phức z1 = 2 + 2i; z2 = 4 - 5i .Tìm phần ảo của số phức w = z1.z2
A. 4.
B. -1.
C. -2.
D. 1.
Câu 11:
Cho hai số phức z1 = 1 - i; z2 = 5 - 2i . Tìm phần ảo của số phức
A. b = -4.
B. b = 8.
C. b = 0.
D. b = -21.
Câu 12:
Cho hai số phức z1 = 1 + i; z2 = 4 - i. Tim số phức
A. z = 2 + 8i.
B. z = 2 - 8i.
C. z = 5 + 3i.
D. z = 3 + 3i.
Câu 17:
Cho số phức z = 6 - 8i. Tìm số phức
A. w = -3 + 2i.
B. w = 2 + 2i.
C. w = -2 - 2i.
D. w = 2 - 2i.
Câu 18:
Cho số phức . Tìm số phức
A. w = -1 + 4i.
B. w = 9 - 2i.
C. w = 4 + 7i.
D. w = 4 - 7i.
Câu 21:
Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z.
A. a = 2.
B. a = -3.
C. a = -2.
D. a = 3.
Câu 22:
Tìm số phức z =(2 - i) 3 - ( 2i + 1) 2
A. z= -5 + 15i.
B. z = 5 - 15i.
C. z = 3 - 8i.
D. z = 3 + 8i.
Câu 23:
Cho số phức z = (1 - i) ( 2i - 8) . Tìm số phức
A. w = 10 - 10i.
B. w = -3 - 3i.
C. w = 16 - 16i.
D. w = -16 - 16i.
Câu 24:
Cho số phức z = ( 2 + i)( 3 - i). Tìm phần thực a và phần ảo b của số phức
A. a = 7 ; b = 1.
B. a = 7 ; b = -1.
C. a = - 7; b = 1.
D. a = -7; b = - 1.
Câu 27:
Cho số phức . Tìm phần thực a và phần ảo b của số phức
A. a = 2; b = 6.
B. a = -2; b = -6.
C. a = -2; b = 6.
D. a = 2; b = -3.
Câu 30:
Tìm các số phức z thỏa mãn và
A. z1 = -1 + i; z2 = 1 - i.
B. z1 = 1 + i; z2 = -1 - i.
C. z1 = -1 + i; z2 = -1 - i.
D. z1 = 1 + i; z2 = 1 - i.
Câu 2:
Cho số phức z thỏa mãn điều kiện . Môđun của số phức W = 1 + 2z + z2 có giá trị là:
A. 10.
B. -10.
C. 100.
D. -100.
Câu 4:
Cho hai số phức z1 = 3 - 2i; z2 = -2 + i Tính P = | z1 + z2|.
A. P = 2.
B.
C. P = 1/2.
D. P = 2.
Câu 5:
Cho hai số phức z1 = 3 + i; z2 = 2 - i. Tính P = | z1 + z1 z2|.
A. P = 10.
B. P = 50.
C. P = 5.
D. P = 85.
Câu 6:
Cho số phức z thỏa mãn điều kiện: . Phần ảo của số phức w = 1 - iz + z là
A. 1.
B. -3.
C. -2.
D. -1.
Câu 7:
Tìm phần thực, phần ảo của số phức z thỏa ( – i)(1 - i) = ( 1 + i) 3979
A. Phần thực là 21990 và phần ảo là 2.
B. Phần thực là - 21990 và phần ảo là 2.
C. Phần thực là -21989 và phần ảo là 1.
D. Phần thực là 21989 và phần ảo là 1.
Câu 8:
Cho số phức z thỏa z = 1+ i+ i2+ i3+...+ i2016. Khi đó phần thực và phần ảo của z lần lượt là
A. 0 và -1.
B. 0 và 1.
C. 1 và 1.
D. 1 và 0.
Câu 10:
Cho số phức z = 1+ ( 1+ i) + ( 1+i) 2+ ...+ (1+ i) 26 . Phần thực của số phức z là
A.
B.
C.
D.
Câu 11:
Cho số phức z = x + y.i thỏa mãn z3 = 2 - 2i. Cặp số là(x;y)
A. (2; 2).
B. (-1; -1).
C. (3;-3).
D. (2; -3).
Câu 12:
Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A.
B. ![]()
C. 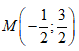
D. 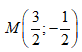
Câu 13:
Gọi A là điểm biểu diễn của số phức z = 3 + 2i và B là điểm biểu diễn của số phức w = 2 + 3i. Trong các khẳng định sau, khẳng định nào đúng?
A. Hai điểm A và B đối xứng nhau qua trục tung.
B. Hai điểm A và B đối xứng nhau qua gốc tọa độ O.
C. Hai điểm A và B đối xứng nhau qua đường thẳng y = x.
D. Hai điểm A và B đối xứng nhau qua trục hoành.
Câu 14:
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A.
B.
C.
D.
Câu 15:
Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – (1+ i)| = |z + 2i| là đường nào sau đây?
A. Đường thẳng.
B. Đường tròn.
C. Elip.
D. Parabol.
Câu 16:
Tìm tập hợp những điểm M biểu diễn số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện
A. Tập hợp những điểm Mlà đường thẳng có phương trình 4x + 2y + 3 = 0.
B. Tập hợp những điểm M là đường thẳng có phương trình 4x - 2y + 3 = 0.
C. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y - 3 = 0.
D. Tập hợp những điểm M là đường thẳng có phương trình 2x + 4y + 3 = 0.
Câu 17:
Tập hợp các điểm M biểu diễn số phức z thoả mãn |z – 2 + 5i| = 4 là:
A. Đường tròn tâm I(2 ; -5) và bán kính bằng 2.
B. Đường tròn tâm I(-2 ; 5) và bán kính bằng 4.
C. Đường tròn tâm I(2 ; -5) và bán kính bằng 4.
D. Đường tròn tâm O và bán kính bằng 2.
Câu 18:
Cho z là số phức thỏa mãn là số thuần ảo. Tìm khẳng định đúng
A.
B. |z| = 1
C. |z| = 2
D.
Câu 19:
Cho số phức z thỏa mãn là số thực. Khẳng định nào sau đây sai
A. z là số thực.
B. z là số ảo.
C. |z| = z.
D.
Câu 20:
Cho các số thực a; b; c và d thỏa mãn: a+ bi= ( c+ di) n. Tìm khẳng định đúng
A. a2 + b2 = 2( c2 + d2) n
B. a2 + b2 = c2 + d2
C. a2 + b2 = 2n( c2 + d2)
D. a2 + b2 = ( c2 + d2)n
Câu 26:
Giải phương trình sau đây (2 + i)z = z + 2i - 1
A. z = 1 + i.
B. z = + i.
C. z = 2+ i.
D. Đáp án khác.
Câu 27:
Tìm tổng phần thực và phần ảo của số phức z thỏa mãn: (1 - i) ( z - 2i) = 2 + i.
A. 4.
B. 3.
C. 5.
D. 7.
Câu 29:
Tính tổng phần thực và phần ảo cùa số phức z thỏa mãn điều kiện sau:
A. 15.
B. 20.
C. 23.
D. 27.
Câu 30:
Phần thực của số z thỏa mãn phương trình: (5 - 4i) z = ( 3 + 2i)(4 - i) gần với giá trị nào nhất.
A. 1,21.
B. 1,22.
C. 1,23.
D. 1,24.
Câu 1:
Phần ảo của số z thỏa mãn phương trình: ( z + 2)i = ( 3i - z)( -1 + 3i) gần với giá trị nào nhất.
A. 2,11.
B. 2,21.
C. 2,31.
D. 2,41.
Câu 2:
Cho phương trình sau: .Tính tổng tất cả các phần thực của các nghiệm của phương trình.
A. 2
B. 3
C. 4
D. 5
Câu 3:
Cho số phức z thỏa mãn ( 3+ i) z = 2. Tính mô-đun của số phức w = z + - i.
A. 1.
B. 2.
C.
D.
Câu 4:
Cho số phức z thỏa mãn điều kiện . Tìm phần thực của số phức w = 4z
A. 7.
B. 8.
C. 10.
D. 11.
Câu 8:
Tìm nghiệm của phương trình:
A. z = 1; z = i.
B. z = -1; z = i.
C. z = -i; z = 1.
D. z = -1; z = -i
Câu 11:
Tính tổng các phần ảo của các số phức z thỏa mãn phương trình
A. 0.
B. 1.
C. 2.
D. 4.
Câu 12:
Cho số phức z thỏa mãn: . Tìm khẳng định đúng?
A. Có 2 số phức z thỏa mãn.
B. các số phức đó là số thực.
C. Các số phức đó là số ảo.
D. Tất cả sai.
Câu 14:
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Câu 15:
Số phức z thỏa mãn phương trình có phần thực và phần ảo lần lượt là:
A: -2; 5
B. -2 và 3
C. 2 và -3
D. 3 và 5
Câu 18:
Xác định tập hợp các điểm trong mặt phẳng biểu diễn số phức z thoả điều kiện |z + 1 – 3i| ≤ 4.
A. Hình tròn tâm I(-1;3), bán kính r = 4.
B. Đường tròn tâm I(-1;3), bán kính r = 4.
C. Hình tròn tâm I(-1; -3), bán kính r = 4.
D. Đường tròn tâm I(1;3), bán kính r = 4.
Câu 20:
Với mọi số ảo z, số z2 + |z|2 là :
A. Số thực âm
B. Số 0
C. Số thực dương
D. Số ảo khác 0
Câu 1:
Tìm số phức z thỏa mãn hệ thức và
A. z = 3 + 4i; z = 5.
B. z = 3 + 4i; z = -4.
C. z = -3 + 4i; z = 5.
D. z = 3 - 4i; z = -5.
Câu 2:
Tìm số thực x; y để hai số phức z1 = 9y2 – 4 – 10xi5 và z2 = 8y2 + 20i11 là liên hợp của nhau?
A. x = -2; y = 2.
B. x = 2; y = ±2.
C. x = 2; y = 2.
D. x = -2; y = ±2.
Câu 4:
Cho số phức z thỏa . Viết z dưới dạng z = a + bi. Khi đó tổng a + b có giá trị bằng bao nhiêu?
A. 3.
B. -1.
C. 1.
D. 2.
Câu 6:
Tìm số phức z để
A. z = 0; z = 1 - i.
B. z = 0; z = 1 + i.
C. z = 0; z = 1 + i; z = 1 - i.
D. z = 1+ i; z = 1- i.
Câu 7:
Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
A. 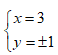
B. 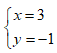
C. 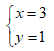
D. 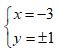
Câu 8:
Cho số phức z = 3+ i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A. 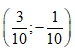
B. 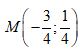
C. 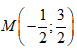
D. 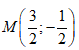
Câu 9:
Căn bậc hai của số phức z = -3 + 4i có kết quả:
A. 1 + 2i.
B. 1 - 2i.
C. 1 + 3i.
D. Tất cả sai.
Câu 11:
Cho z = 3 + 4i. Tìm căn bậc hai của z.
A. -2 + i và 2 - i
B. 2 + i và 2 - i
C. 2 + i và -2 - i
D. 3 - 2i và 2 - 3i
Câu 12:
Gọi z là căn bậc hai có phần ảo âm của 33 - 56i. Phần thực của z là:
A. 6.
B. 7.
C. 4.
D. –4.
Câu 16:
Trong C, phương trình (z2 + i) (z2 – 2iz – 1) = 0 có nghiệm là:
A. ![]()
B. 1 - i; -1+ i; 2i
C. 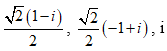
D. 1 - 2i; -15i; 3i
Câu 20:
Gọi z1; z2 là hai nghiệm phức của phương trình z2 - 4z + 9 = 0; gọi M và N lần lượt là các điểm biểu diễn z1; z2 trên mặt phẳng phức. Tính độ dài đoạn thẳng MN.
A. 1
B. 2
C.
D.
Câu 21:
Tìm các số thực b,c để phương trình z2 + bz + c = 0 nhận z = 1+ i làm một nghiệm.
A. b = -2; c = 3
B. b = -1; c = 2
C. b = -2; c = 2
D. b = 2; c = 2
Câu 8:
Trong C, nghiệm của phương trình z2 = -5 + 12i là:
A. 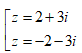
B. z = 2 + 3i
C. z = 2 - 3i
D. 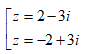
Câu 9:
Trong C, phương trình z4 – 6z2 + 25 = 0 có nghiệm là:
A. ±8; ± 5i
B. ±3; ± 4i
C. ±5; ± 2i
D. ±(2 + i); ± (2 – i)
Câu 10:
Biết z1 , z2 là hai nghiệm của phương trình 2. Khi đó giá trị của là:
A. 9/4.
B. 9.
C. 4.
D. -9/4.
Câu 11:
Gọi z1 ; z2 là hai nghiệm phức của phương trình z2 - 4z+ 5= 0. Khi đó phần thực của là:
A. 5.
B. 6.
C. 4.
D.7.
Câu 13:
Trong C, phương trình |z| + z = 2 + 4i có nghiệm là:
A. z = -3 + 4i
B. z = -2 + 4i
C. z = -4 +4i
D. z = -5 + 4i
Câu 16:
Trong C, phương trình z4 – 1 = 0 có nghiệm là:
A. ± 1; ± 2i
B. ± 2; ± 2i
C. ± 3; ± 4i
D. ± 1; ± i
Câu 17:
Phương trình z3 = 8 có bao nhiêu nghiệm phức với phần ảo âm?
A. 1.
B. 2.
C. 3.
D. 0.
Câu 18:
Trong C, phương trình z4 + 4= 0 có nghiệm là:
A. ±(1 - 4i) ; ±(1 + 4i)
B. ±(1 - 2i) ; ±(1 + 2i)
C. ±(1 - 3i) ; ±(1 +3i)
D. ±(1 - i) ; ±(1 + i)
Câu 19:
Tập nghiệm trong C của phương trình z3 + z2 + z + 1 = 0 là:
A.{-1; -i ; i}
B.{-1 ; 1 ; i}
C. -1 ; i
D. 1 ; -1 ; i ; -i
Câu 20:
Phương trình (2 + i) z2 + az + b = 0 có hai nghiệm là 3 + i và 1 - 2i. Khi đó a = ?
A. -9 - 2i.
B. 15 + 5i.
C. 9 + 2i.
D. 15 - 5i.
Câu 21:
Giá trị của các số thực b ; c để phương trình z2 + bz + c = 0 nhận số phức z =1 + i làm một nghiệm là:
A. 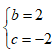
B. 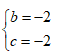
C. 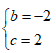
D. 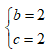
Câu 22:
Trên tập hợp số phức, phương trình z2 + 7z + 15 = 0 có hai nghiệm . Giá trị biểu thức z1 + z2 + z1z2
A. –7
B. 8
C. 15
D. 22
Câu 23:
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Câu 24:
Giả sử z1 , z2 là hai nghiệm của phương trình z2 - 2z + 5 = 0 và A, B là các điểm biểu diễn của z1 , z2 . Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(1;1)
B. I(-1;0)
C. I(0;1)
D. I(1;0)
Câu 1:
Cho hai số phức z1; z2 khác 0 thỏa mãn .Gọi A; B lần lượt là các điểm biểu diễn cho số phức z1; z2. Khi đó tam giác OAB là:
A. Tam giác đều.
B. Tam giác vuông tại O.
C. Tam giác tù.
D. Tam giác có một góc bằng 45o.
Câu 4:
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
A. 3.
B. 2.
C. 4.
D. 1.
Câu 5:
Gọi z1 ; z2 ; z3 ; z4 là các nghiệm phức của phương trình .
Giá trị của là:
A. 17/8
B. 17/9
C. 9/17
D. 17i/9
Câu 6:
Cho số phức z; w thỏa mãn |z – 1 + 2i| = |z + 5i| ; w = iz + 20. Giá trị nhỏ nhất m của |w| là?
Câu 7:
Xét các số phức z thỏa mãn thiết | z + 2 - i| + | z - 4 - 7i|= . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z – 1 + i|. Tính P = m + M.
Câu 8:
Cho số phức z thỏa mãn điều kiện |z -2 + 2i | + | z + 1 -3i | = . Hãy tìm giá trị lớn nhất, giá trị nhỏ nhất của |z + 1 + i|.
A.
B.
C.
D. Đáp án khác.
Câu 9:
Cho số phức z thoả mãn |z – 1 + 3i| + |z + 2 – i| = 8. Tìm giá trị lớn nhất, giá trị nhỏ nhất của P = |2z + 1 + 2i|.
A. 8 và 4
Câu 11:
Cho số phức z thỏa mãn |z – 1 – 2i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của |z + 2 + i|. Tính S = m2 + M2?
A. 34
B. 82
C. 68
D. 36
Câu 12:
Cho số phức z thỏa mãn |(1+ i )z + 1 -7i | = . Tìm giá trị lớn nhất của |z|?
A. 4
B. 3
C. 7
D. 6
Câu 13:
Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn ![]() là đường tròn C. Khoảng cách từ tâm I của đường tròn (C) đến trục tung bằng bao nhiêu?
là đường tròn C. Khoảng cách từ tâm I của đường tròn (C) đến trục tung bằng bao nhiêu?
A. d(I; Oy) = 1.
B. d(I ; Oy) = 2.
C. d(I ; Oy) = 0.
D.
Câu 14:
Số phức z thỏa mãn điều nào thì có điểm biểu diễn thuộc phần gạch chéo như trên hình.
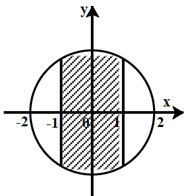
A. Số phức z = a + bi; |z| ≤ 2; -1 ≤ a ≤ 1.
B. Số phức z = a + bi; |z| ≤ 2; a < -1; a > 1.
C. Số phức z = a + bi; |z| < 2; -1 ≤ a ≤ 1.
D. Số phức z = a + bi; |z| ≤ 2; -1 ≤ b ≤ 1.
Câu 15:
Trong mặt phẳng phức Oxy, số phức z thỏa điều kiện nào thì có điểm biểu diễn số phức thuộc phần tô màu như hình vẽ
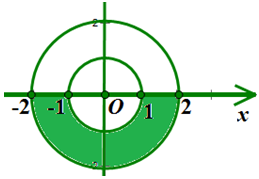
A. 1 ≤ |z| ≤ 2 và phần ảo dương.
B. 1 ≤ |z| ≤ 2 và phần ảo âm.
C. 1 < |z| < 2 và phần ảo dương.
D. 1 < |z| < 2 và phần ảo âm.
Câu 16:
Cho số phức z thỏa mãn |z – 4| + |z + 4| = 10. Giá trị lớn nhất và nhỏ nhất của mô – đun của số phức z là
A. 10 và 4
B. 5 và 4
C. 4 và 3
D. 5 và 3
Câu 17:
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để ![]() với số phức z có phần thực không âm. Tính diện tích hình (H).
với số phức z có phần thực không âm. Tính diện tích hình (H).
Câu 18:
Có số phức z có phần ảo bằng 164 và n ∈ R* thỏa mãn: . Tìm n?
A. 679
B. 697
C. 567
D. Đáp án khác
Câu 19:
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | + 3 + 4i| và là một số thuần ảo.
Câu 20:
Trong các số phức z thỏa mãn điều kiện | z - 2 + 3i | = . Số phức z có mođun nhỏ nhất có phần thực gần với giá trị nào nhất?
A. 1,17
B. 1,16
C. 1,15
D. 1,14
Câu 21:
Tìm số phức z thỏa mãn (z - 1)( + 2i) là số thực và |z| đạt giá trị nhỏ nhất.
A. z = 1+ 2i
Câu 22:
Trong các số phức z thỏa mãn |z - 3i| + | i + 3| =10 , tìm số phức z có mô-đun nhỏ nhất.
A. z = 2 hoặc – 2
B. z= 3 hoặc – 3
C. z = 4 hoặc – 4
D. tất cả sai
Câu 23:
Trong các số phức z thỏa mãn | z - 2 + i | = | + 1 -4i | , tìm số phức có mô-đun nhỏ nhất.
A. z = 1
B. z = 1 - i
C. z = -1 - i
D. z = 2 - i
Câu 25:
Cho số phức z thỏa mãn |z – 2- 3i| = 1. Giá trị lớn nhất của ![]() là?
là?
A.
B. 4
C. 6
D.
Câu 1:
Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
A. 8i
B. 4
C. -8
D. 8
Câu 2:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức
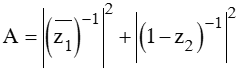
A. 0,5
B. 1,5
C. 1
D. 2
Câu 3:
Gọi z1; z2 lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức ![]()
A. 1
B. 3
C. 0
D. 5
Câu 4:
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
Câu 5:
Cho số phức z1; z2 thỏa mãn 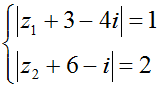 . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?
. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 - z2 | là?
A. 18
B.
C. 6
D.
Câu 6:
Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.
Câu 7:
Cho số phức z thỏa mãn  . Giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là.
. Giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là.
Câu 8:
Cho số phức z thỏa mãn ![]() là một số thực. Hỏi giá trị nhỏ nhất của |z| gần với giá trị nào nhất?
là một số thực. Hỏi giá trị nhỏ nhất của |z| gần với giá trị nào nhất?
A. 2,7
B. 2,8
C. 1,3
D. 1,4
Câu 9:
Trong các số phức z thỏa mãn |z + 4 - 3i| + |z -8 - 5i| = 2. Tìm giá trị nhỏ nhất của |z – 2 – 4i| ?
A. 1/2
B. 5/2
C. 2
D. 1
Câu 10:
Cho hai số phức z1 và z2 thỏa mãn | z1 + 2 z2| = 5 và |3 z1 - z2| = 3. Giá trị lớn nhất của P = | z1| + | z2| gần với số nguyên nào nhất?
A. 2
B. 3
C.4
D. 5
Câu 11:
Cho số phức với m nguyên. Có bao nhiêu giá trị của m với 1≤ m≤ 50 để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Câu 12:
Cho biểu thức L = 1- z+ z2- z3+ ...+ z2016- z2017 với 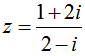 . Biểu thức L có giá trị là
. Biểu thức L có giá trị là
A. 1 - i.
B. 1 + i.
Câu 13:
Cho 2 số phức 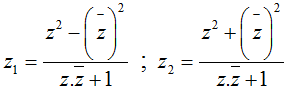 ; với z = x+ yi.
; với z = x+ yi.
Mệnh đề nào sau đây đúng?
A. z1 và z2 là số thuần ảo.
B. z2 là số thuần ảo.
C. z1 là số thuần ảo.
D. z1 và z2 là số thực.
Câu 16:
Cho số phức z thỏa mãn |z +1 +i | =| - 2i |. Tìm giá trị nhỏ nhất của |z|.
A.
B. 1
C.
D. 2
Câu 18:
Cho số phức z thỏa mãn |z – 1 – 2i| = 2. Giá trị lớn nhất của T = |z| + |z – 3 – 6i| gần với giá trị nào nhất?
A. 6
B. 7
C. 8
D. 9
Câu 19:
Cho số phức z thỏa mãn | z -3 - 4i| = .Tìm |z| để biểu thức: P = |z + 2|2 - |z – i|2 đạt giá trị lớn nhất?
B. 10
Câu 20:
Tìm mô-đun của số phức w = b + ci biết số phức 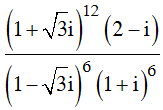 là nghiệm của phương trình z2 + 8bz + 64c = 0
là nghiệm của phương trình z2 + 8bz + 64c = 0
A.
B. 7
C.
D.
Câu 21:
Cho a,b,c là 3 số phức phân biệt khác 0 và modul của chúng bằng nhau .Nếu một nghiệm của phương trình az2 + bz + c = 0 có môđun bằng 1 thì khẳng định nào sau đây đúng.
A. c2 = ab
B. a2 = bc
C. b = ac
D. b2 = ac
Câu 22:
Cho số phức z thỏa mãn ![]() là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:
là số thuần ảo. Tập hợp các điểm M biểu diễn số phức z là:
A. Đường tròn tâm O, bán kính R = 1.
B. Hình tròn tâm O, bán kính R = 1 (kể cả biên).
C. Hình tròn tâm O, bán kính R = 1 (không kể biên).
D. Đường tròn tâm O, bán kính R = 1 bỏ đi một điểm (0;1).
Câu 23:
Cho số phức z thỏa mãn điều kiện |z – 3 + 4i| ≤ 2. Trong mặt phẳng Oxy tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích
A. S = 9π.
B. S = 12π.
C. S = 16π.
D. S = 25π.
Câu 24:
Trong mặt phẳng phức Oxy, tâp hợp các điểm biểu diễn số phức z sao cho z 2 là số thuần ảo là hai đường thẳng d1 ; d2. Góc α giữa 2 đường thẳng d1 ; d2 là bao nhiêu?
A. α = 450.
B. α = 600.
C. α = 900.
D. α = 300.
Câu 25:
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z + 2| + |z – 2| = 5 trên mặt phẳng tọa độ là một
A. đường thẳng.
B. đường tròn.
C. elip.
D. hypebol.
Câu 1:
Trên mặt phẳng tọa độ Oxy, tìm tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10.
A. Đường tròn ( x - 2) 2 + ( y + 2) 2 = 100.
B. Elip
C. Đường tròn ( x -2) 2 + ( y + 2) 2 = 10.
D. Elip
Câu 2:
Cho số phức z thỏa mãn |z + 2| + |z – 2| = 8. Trong mặt phẳng phức tập hợp những điểm M biểu diễn cho số phức z là?
C. ( x + 2) 2 + ( y - 2) 2 = 64.
D. ( x + 2) 2 + ( y - 2) 2 = 8.
Câu 4:
Tìm nghiệm của phương trình: ( z + 3 - i)2 - 6( z + 3 - i) + 13 = 0
A. z = 3i; z = 1 - 2i
B. z = - i; z = 3i + 4
C. z = 3i + 4; z = 3i
D. z = 3i; z = -i
Câu 5:
Tìm nghịch đảo của số phức z, biết z thỏa mãn | z - 2i| =| + 2 + 4i| và là số thuần ảo.
Câu 6:
Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa mãn ![]() là đường tròn C. Diện tích S của đường tròn C bằng bao nhiêu?
là đường tròn C. Diện tích S của đường tròn C bằng bao nhiêu?
A. S = 4π.
B. S = 2π.
C. S = 3π.
D. S = π.
Câu 7:
Tính giá trị của ![]() biết z1; z2; z3; z4 là nghiệm phức của phương trình ( 5z2 - 6iz - 2)( -3z2+ 2iz) = 0.
biết z1; z2; z3; z4 là nghiệm phức của phương trình ( 5z2 - 6iz - 2)( -3z2+ 2iz) = 0.
A. 12/25
B. 13/45
C. 11/23
D. 26/7
Câu 10:
Giải phương trình sau: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
D. Cả A và C đúng
Câu 11:
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Câu 12:
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1 + 7i.
B. 5 + i.
C. 1 + 5i.
D. 3 + 5i.
Câu 13:
Cho 3 điểm A ; B ;C lần lượt biểu diễn cho các số phức z1 ; z2 ; z3 .Biết | z1| = | z2| = | z3| và z1+ z2= 0 . Khi đó tam giác ABC là tam giác gì?
A. Tam giác ABC đều.
B. Tam giác ABC vuông tại C.
C. Tam giác ABC cân tại C.
D. Tam giác ABC vuông cân tại C.
Câu 16:
Tập hợp các điểm trong mặt phẳng tọa độ biểu diễn số phức z thoả mãn điều kiện: ![]() là hình gì?
là hình gì?
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường Elip.
D. Một đường tròn.
Câu 17:
Cho số phức z = m - 2 + ( m2 - 1) i với m là số thực. Gọi (C) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Tính diện tích hình phẳng giới hạn bởi (C) và Ox.
A. 1.
B. 4/3.
C. 32/3.
D. 8/3.
Câu 18:
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 - z + 3i | . Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip.
Câu 19:
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện 
A. Là đường Hyperbol y = -1/x
B. Là đường Hyperbol y = 1/x
C. Là đường tròn tâm O bán kính R = 4.
D. Là hai đường Hyperbol y = -1/x và y = 1/x
Câu 21:
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3
Câu 22:
Cho số phức z thỏa mãn ( 1 - 3i) z là số thực và ![]() . Hỏi có bao nhiêu số phức z thỏa mãn
. Hỏi có bao nhiêu số phức z thỏa mãn
A. 1
B. 2
C. 3
D. 4
Câu 23:
Tìm số phức z biết |iz + 1 | = và ( 1 + i) z + 1 – 2i là số thuần ảo.
A. z = 1
B. z = 1 + 2i
C. z = - 1 và z = 1+ 2i
D. Đáp án khác
Câu 25:
Biết z1; z2 là số phức thỏa mãn:.
Tính
A. -111/4 + i
B. -111 + i
C. -111+ 4i
D. -44 + i
Câu 2:
Biết z1; z2 là số phức thỏa điều kiện z2 - |z|2 + 1 = 0. Tính 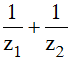
A. –i
B. i
C. 1 + i
D. 0
Câu 3:
Biết z1; z2; z3; z4 là các số phức thỏa điều kiện .
Tính | z1| + | z2| + | z3| + | z4|
A. 3
B. 2
Câu 4:
Cho số phức z thỏa điều kiện 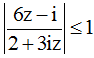 . Tìm khẳng định đúng
. Tìm khẳng định đúng
A. |z| ≥ 1
B. |z| ≤ 3
C. |z| ≤ 1/3
D. |z| > 1/3
Câu 6:
Cho phương trình z2 + mz - 6i = 0. Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + bi). Giá trị a + 2b là:
A. 0
B. 1
C.- 2
D. - 1
Câu 7:
Cho số phức z thỏa mãn điều kiện 11z10 + 10iz9 + 10iz -11 = 0. Tìm khẳng định đúng
A. |z| > 1
B. |z| = 1
C. |z| < 1
D. |z| > 1/3
Câu 8:
Trong tập số phức, giá trị của m để phương trình bậc hai z2 + mz + i = 0 có tổng bình phương hai nghiệm bằng -4i là:
A. ±( 1 - i)
B. 1 - i
C. ±( 1 + i)
D. -1 - i
Câu 9:
Gọi z1 ; z2 là hai nghiệm của phương trình z2 + 2z+ 8= 0, trong đó z1 có phần ảo dương. Giá trị của số phức ![]() là:
là:
A. 12+ 6i
B. 10
C. 10 + 2i
D.12- 6i
Câu 10:
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 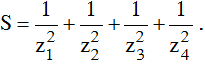
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Câu 11:
Cho z1; z2; z3; z4 là các nghiệm của phương trình: (z2 +1) (z2 - 2z + 2) = 0 . Tính ![]()
A.5
B.4
C.-2
D.3
Câu 22:
Cho z1; z2 là hai nghiệm phức của phương trình z2 - 2z + 4 = 0. Phần thực, phần ảo của số phức: 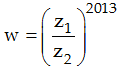 lần lượt là bao nhiêu, biết z1 có phần ảo dương.
lần lượt là bao nhiêu, biết z1 có phần ảo dương.
A. 0; 1
B. 1; 2
C. 1; 0
D. tất cả sai
Câu 23:
Cho số phức z biết z= 1 + . Tìm tổng của phần thực và phần ảo của số phức w = (1 + i)z5
A. 16
B. 19
C. 28
D. 32
Câu 24:
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1
Câu 25:
Cho các số phức z thỏa mãn: (2 - z)5 = z5. Hỏi phần thực của z là bao nhiêu?
A. 0
B.1
C. 2
D. Chưa kết luận được
Câu 26:
Cho phương trình 8z2 - 4(a + 1)z + 4a + 1 = 0 (1) với a là tham số. Tính tổng tất cả các giá trị của a để (1) có hai nghiệm z1; z2 thỏa mãn z1/ z2 là số ảo, trong đó z2 là số phức có phần ảo dương.
A. 1
B. 2
C. 3
D. 4
Câu 1:
Cho hai số phức Phần thực và phần ảo của số phức là
A. 1 và 12
B. -1 và 12
C. –1 và 12i
D. 1 và 12i
Câu 2:
Phần thực và phần ảo của số phức là
A. 1 và 3
B. 1 và -3
C. -2 và
D. 2 và
Câu 4:
Thực hiện phép tính: ta có
A. T = 3 + 4i
B. T = -3 + 4i
C. T = 3 – 4i
D. T = -3 – 4i
Câu 6:
Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2
B. 3 và 2
C. 3 và – 2i
D. 3 và 2i
Câu 9:
Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức: là
A. 2
B. 4
C.
D. 10
Câu 13:
Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2i| = 4 là
A. Đường tròn tâm I(1; -2) bán kính R = 4
B. Đường tròn tâm I(1; 2) bán kính R = 4
C. Đường tròn tâm I(0; 2) bán kính R = 4
D. Đường tròn tâm I(0; -2) bán kính R = 4
Câu 14:
Tập hợp các điểm biểu diễn số phức z thỏa mãn là
A. Đường tròn tâm I(3; 2) bán kính R = 4
B. Đường tròn tâm I(3; -2) bán kính R = 4
C. Đường tròn tâm I(-3; 2) bán kính R = 4
D. Đường tròn tâm I(-3; -2) bán kính R = 4
Câu 2:
Trong các kết luận sau, kết luận nào sai:
A. là một số thực
B. là một số ảo
C. là một số thực
D. là một số ảo
Câu 5:
Trong hình vẽ bên, điểm M biểu diễn số phức z. Số phức là:
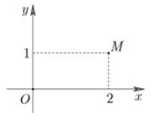
A. 2 - i
B. 1 + 2i
C. 1 - 2i
D. 2 + i
Câu 6:
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo của số phức z
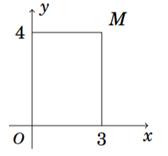
A. Phần thực bằng 4 và phần ảo bằng 3
B. Phần thực bằng 4 và phần ảo bằng 3i
C. Phần thực bằng 3 và phần ảo bằng 4
D. Phần thực bằng 3 và phần ảo bằng 4i
Câu 9:
Cho số phức z có dạng đại số và dạng lượng giác lần lượt là: z = a + bi và , chọn mệnh đề đúng:
A.
B.
C.
D.
Câu 12:
Trong C, cho phương trình (*). Gọi , ta xét các mệnh đề sau:
- Nếu là số thực âm thì phương trình (*) vô nghiệm.
- Nếu thì phương trình (*) có 2 nghiệm phân biệt
- Nếu thì phương trình (*) có 1 nghiệm kép
Trong các mệnh đề trên, mệnh đề nào đúng?
A. Không có mệnh đề nào đúng
B. Có 1 mệnh đề đúng
C. Có 2 mệnh đề đúng
D. Có 3 mệnh đề đúng
Câu 14:
Cho . Chọn mệnh đề đúng:
A. r là acgumen của z
B. r là mô đun của z
C. là acgumen của z
D. là acgumen của z
Câu 15:
Gọi là một acgumen của z, chọn mệnh đề đúng:
A. là một acgumen của z
B. là một acgumen của z
C. là một acgumen của z
D. là một acgumen của z
Câu 3:
Điểm biểu diễn của số phức z là M(1;2). Tọa độ của điểm biểu diễn số phức là:
A. (2; -3)
B. (2; 1)
C. (-1; 6)
D. (2; 3)
Câu 4:
Gọi lần lượt là hai nghiệm của phương trình với có phần ảo dương. Giá trị của biểu thức bằng
A. -9 + 4i
B. -10 + 10i
C. -5
D. 10
Câu 10:
Giả sử là hai nghiệm phức của phương trình và A, B là các điểm biểu diễn của . Tọa độ trung điểm của đoạn thẳng AB là:
A. (0;1)
B. (0;-1)
C. (1;1)
D. (1;0)
Câu 12:
Có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện |z| = 5,
A. 1
B. 2
C. 3
D. 4
Câu 13:
Gọi là 1 acgumen của số phức z có điểm biểu diễn là nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của z?
A.
B.
C.
C.
Câu 14:
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn số phức z thỏa mãn z(1 + i) là số thực là:
A. Đường tròn bán kính bằng 1.
B. Trục Ox.
C. Đường thẳng y = - x.
D. Đường thẳng y = x.
Câu 15:
Cho số phức z có dạng lượng giác là z = . Dạng đại số của z là:
A. z = 4
B. z = -i
C. z = 4i
D. z = -4i
Câu 1:
Cho số phức z thỏa mãn |z + 3 – 4i| = 5. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính của đường tròn đó.
A.
B.
C.
D.
Câu 2:
Tìm số điểm biểu diễn cho số phức z thỏa mãn đồng thời các điều kiện |z + 4| = 3|z| và z là thuần ảo?
A. 1
B. 0
C. 3
D. 2
Câu 3:
Số số phức z thỏa mãn đồng thời các điều kiện và là số thuần ảo là:
A. 1
B. 4
C. 0
D. 2
Câu 4:
Số phức z = x + yi thỏa mãn |z – 2 – 4i| = |z – 2i| đồng thời có mô đun nhỏ nhất là:
A. z = 2 + 2i
B. z = 2 - 2i
C. z = 1 + i
D. z = 1 - i
Câu 5:
Cho các số phức thỏa mãn điều kiện . Giá trị của biểu thức bằng:
A. 8
B. 6
C. 1
D. 2
Câu 6:
Gọi là hai nghiệm phức của phương trình . Tính giá trị của
A. P = 1
B. P = 0
C. P = -1
D. P = 2
Câu 8:
Biết số phức thỏa mãn đồng thời các điều kiện và biểu thức đạt giá trị lớn nhất. Tính |z|
A.
B.
C.
D.
Câu 9:
Cho hai số phức thỏa mãn . Gọi M, N là các điểm biểu diễn cho và . Biết . Tính ?
A.
B.
C.
D.
Câu 10:
Cho hai số phức thỏa mãn và . Tìm giá trị lớn nhất m của biểu thức
A. m = 2
B.
C.
D.
Câu 6:
Trong số các số phức z thỏa mãn điều kiện , gọi là số phức có mô đun lớn nhất. Khi đó là:
A. 3
B. 4
C. 5
D. 8
Câu 7:
Trong các số phức z thỏa mãn , gọi là số phức có mô đun nhỏ nhất. Khi đó:
A. Không tồn tại số phức
B.
C.
D.
Câu 8:
Cho các số phức và z thỏa mãn . Biểu thức đạt giá trị nhỏ nhất khi . Hiệu a - b bằng:
A.
B.
C.
D.
Câu 10:
Cho số phức z thỏa mãn , số phức w thỏa mãn . Tính giá trị nhỏ nhất của
A.
B.
C.
C.
Câu 11:
Xét các số phức thỏa mãn điều kiện . Tính a + b khi đạt giá trị nhỏ nhất.
A.
B.
C. 3
D.
Câu 12:
Cho các số phức w, z thỏa mãn và . Giá trị lớn nhất của biểu thức bằng:
A.
B.
C.
D.
Câu 13:
Cho số phức z thỏa điều kiện . Giá trị nhỏ nhất của biểu thức P = được viết dưới dạng với a, b là các hữu tỉ. Giá trị của a + b là:
A. 4
B. 2
C. 7
D. 3
Câu 14:
Cho các số phức z, w thỏa mãn . Tìm giá trị lớn nhất của biểu thức
A.
B.
C.
D.
Câu 1:
Cho số phức z thay đổi thỏa mãn . Gọi S là đường cong tạo bởi tất cả các điểm biểu diễn số phức khi z thay đổi. Tính diện tích hình phẳng giới hạn bởi đường cong S.
A.
B.
C.
D.
Câu 3:
Cho là ba số phức thay đổi thỏa mãn . Trong mặt phẳng phức A, B biểu diễn . Giả sử O, A, B lập thành tam giác có diện tích là a, chu vi là b. Giá trị lớn nhất của biểu thức là:
A.
B.
C.
D.
Câu 4:
Cho các số phức thỏa mãn và chúng được biểu diễn trong mặt phẳng phức lần lượt là các điểm M, N. Biết góc giữa vec tơ và bằng . Tìm mô đun của số phức ?
A.
B.
C.
D.
Câu 5:
Cho thỏa mãn . Biết tập hợp các điểm biểu diễn cho số phức là đường tròn tâm I, bán kính R. Kết quả nào đúng?
A.
B.
C.
D.
Câu 6:
Trong các số phức z thỏa mãn , gọi lần lượt là các số phức có mô đun lớn nhất và nhỏ nhất. Khi đó mô đun lớn nhất của số phức là:
A.
B.
C.
D.
Câu 7:
Cho số phức z thỏa mãn , số phức w thỏa mãn . Tính giá trị nhỏ nhất của
A.
B.
C.
D.
Câu 9:
Cho số phức z thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất biểu thức . Mô đun của số phức là:
A.
B.
C.
D.
Câu 10:
Cho các số phức và số phức z thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Giá trị biểu thức bằng:
A. 15
B. 7
C. 8
D. 11
Câu 12:
Cho các số phức với . Tập hợp các điểm biểu diễn số phức là đường tròn tâm là gốc tọa độ và bán kính bằng 1. Tập hợp các điểm biểu diễn số phức z là:
A. Đường tròn tâm là điểm biểu diễn số phức và bán kính bằng
B. Đường tròn tâm là gốc tạo độ và bán kính bằng
C. Đường tròn tâm là gốc tạo độ và bán kính bằng
D. Đường tròn tâm là điểm biểu diễn số phức và bán kính bằng
Câu 13:
Cho số phức z thỏa mãn . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của . Khi đó bằng:
A. 5
B. 15
C. 10
D. 20
Câu 14:
Cho số phức z thay đổi thỏa mãn . Gọi S là đường cong tạo bởi tất cả các điểm biểu diễn số phức khi z thay đổi. Tính diện tích hình phẳng giới hạn bởi đường cong S.
A.
B.
C.
D.
Câu 2:
Cho là ba số phức thay đổi thỏa mãn và . Trong mặt phẳng phức A, B biểu diễn . Giả sử O, A, B lập thành tam giác có diện tích là a, chu vi là b. Giá trị lớn nhất của biểu thức là:
A.
B.
C.
D.
Câu 3:
Cho các số phức thỏa mãn và chúng được biểu diễn trong mặt phẳng phức lần lượt là các điểm M, N. Biết góc giữa vec tơ bằng . Tìm mô đun của số phức ?
A.
B.
C.
D.
Câu 4:
Xét các số phức thỏa mãn đồng thời hai điều kiện và đạt giá trị nhỏ nhất. Giá trị là:
A.
B.
C.
D.
Câu 5:
Giả sử là hai trong số các số phức z thỏa mãn và . Giá trị lớn nhất của bằng:
A. 3
B.
C.
D. 4
Câu 6:
Cho các số phức w, z thỏa mãn . Giá trị lớn nhất của biểu thức bằng:
A.
B.
C.
D.
Câu 9:
Cho số phức z thỏa mãn điều kiện . Tìm giá trị lớn nhất của biểu thức
A.
B.
C.
D.

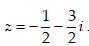
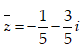
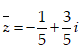
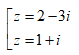
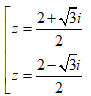
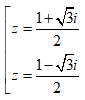

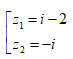

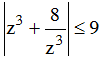 .Tìm khẳng định đúng
.Tìm khẳng định đúng