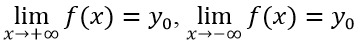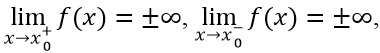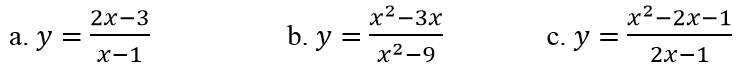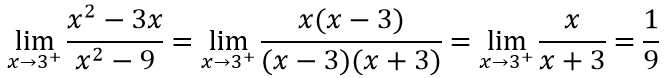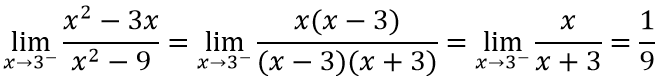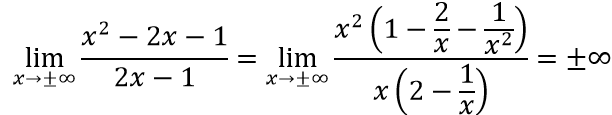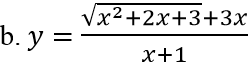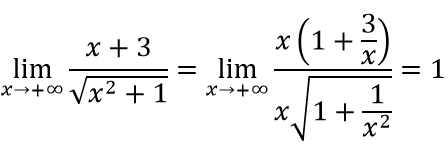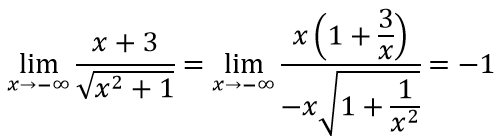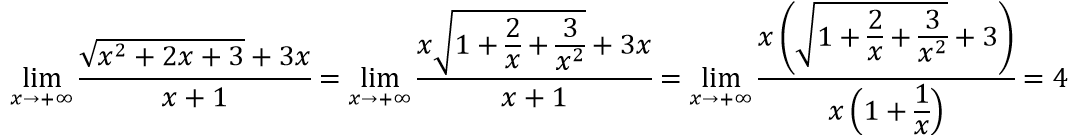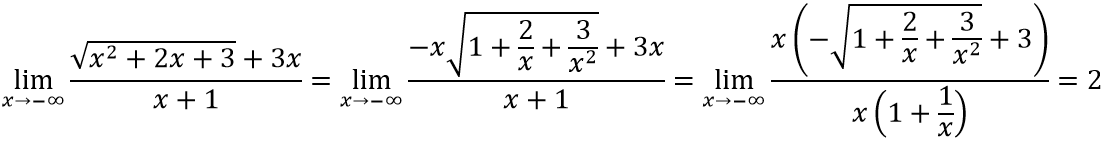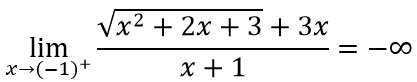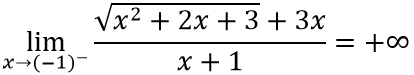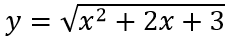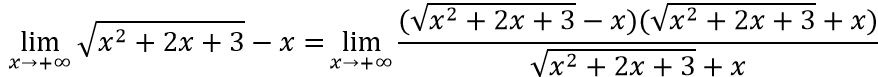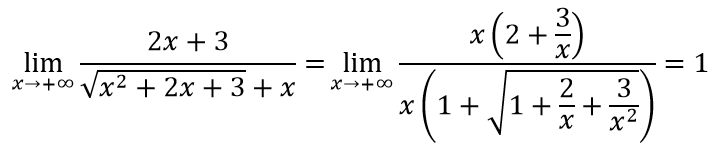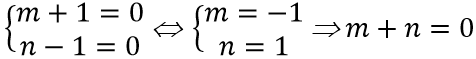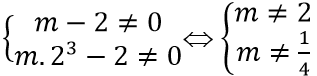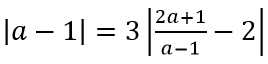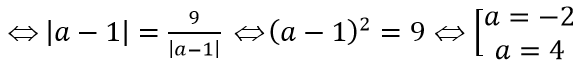Các dạng bài tập Tiệm cận của đồ thị hàm số chọn lọc, có đáp án - Toán lớp 12

Các dạng bài tập Tiệm cận của đồ thị hàm số chọn lọc, có đáp án

Với Các dạng bài tập Tiệm cận của đồ thị hàm số chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tiệm cận của đồ thị hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

• 100 Bài tập Tiệm cận của đồ thị hàm số có lời giải (nâng cao) Xem chi tiết
• 100 Bài tập Tiệm cận của đồ thị hàm số có lời giải (cơ bản) Xem chi tiết
• 5 dạng bài Tìm tiệm cận của hàm số trong đề thi Đại học có lời giải Xem chi tiết
• Dạng 1: Xác định tiệm cận Xem chi tiết
• Trắc nghiệm tìm tiệm cận của đồ thị hàm số Xem chi tiết
• Dạng 2: Tìm tham số m để hàm số có tiệm cận Xem chi tiết
• Trắc nghiệm tìm tham số m để hàm số có tiệm cận Xem chi tiết
• Dạng 3: Các bài toán liên quan đến tiệm cận của hàm số Xem chi tiết
• Trắc nghiệm về tiệm cận của hàm số Xem chi tiết
• Cho bảng biến thiên tìm đường tiệm cận đứng, tiệm cận ngang cực hay, có lời giải Xem chi tiết

Cách tìm tiệm cận của đồ thị hàm số

A. Phương pháp giải & Ví dụ

1. Đường tiệm cận ngang

        Cho hàm số y = f(x) xác định trên một khoảng vô hạn (là khoảng dạng (a; +∞),(-∞; -b) hoặc (-∞; +∞). Đường thẳng y = y₀ là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

        Nhận xét: Như vậy để tìm tiệm cận ngang của đồ thị hàm số ta chỉ cần tính giới hạn của hàm số đó tại vô cực.

2. Đường tiệm cận đứng

        Đường thẳng x = x₀ được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn

Ví dụ minh họa

Ví dụ 1: Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau

Hướng dẫn:

a. Ta có:

là tiệm cận ngang của đồ thị hàm số.

là tiệm cận đứng của đồ thị hàm số.

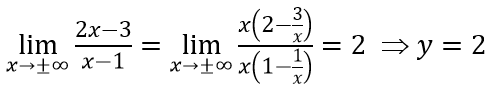
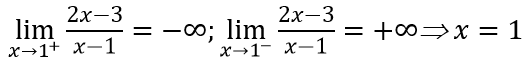
b. Ta có:

là tiệm cận ngang của đồ thị hàm số.

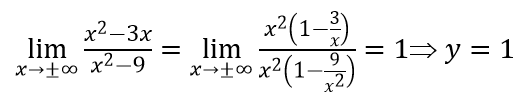
⇒ Đồ thị hàm số không có tiệm cận đứng

c. Ta có:

⇒ Đồ thị hàm số không có tiệm cận ngang.

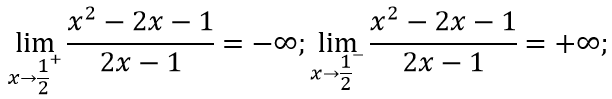
⇒ x = 1/2 là tiệm cận đứng của đồ thị hàm số.

Ví dụ 2: Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau

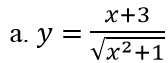
Hướng dẫn:

a. Ta có:

⇒ y = 1; y = -1 là tiệm cận ngang của đồ thị hàm số.

Đồ thị hàm số không có tiệm cận đứng.

b. Ta có:

⇒ y = 4; y = 2 là tiệm cận ngang của đồ thị hàm số.

⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.

Ví dụ 3: Tìm các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau

a. 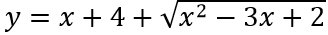    b.

Hướng dẫn:

a. Đồ thị hàm số không có tiệm cận đứng

⇒ y = 11/2 là tiệm cận ngang của đồ thị hàm số

b. Đồ thị hàm số không có tiệm cận đứng

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số.

Tìm tham số m để hàm số có tiệm cận

A. Phương pháp giải & Ví dụ

Ví dụ minh họa

Ví dụ 1.(THPT Chuyên Bảo Lộc – Lâm Đồng 2017). Cho hàm số 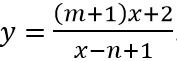. Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Tính giá trị biểu thức P = m + n.

Hướng dẫn

Đồ thị hàm số có tiệm cận ngang y = m + 1 và tiệm cận đứng x = n - 1. Do đó đồ thị hàm số nhận trục tung x = 0 và trục hoành y = 0 làm tiệm cận khi và chỉ khi

Ví dụ 2 (THPT chuyên Thái Nguyên 2017 L2). Tìm m để đồ thị hàm số 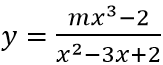có hai đường tiệm cận đứng.

Hướng dẫn

Ta có x² - 3x + 2 = 0 ⇔ x = 1 hoặc x = 2

Để hai đường thẳng x = 1 và x = 2 là đường tiệm cận của đồ thị hàm số thì x = 1 và x = 2 không là nghiệm của tử số mx³ - 2. Tức là:

Ví dụ 3: Tìm tất cả các giá trị của tham số m để đồ thị hàm số 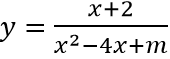có tiệm cận ngang mà không có tiệm cận đứng.

Hướng dẫn

Ta có 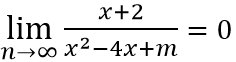nên y = 0 là tiệm cận ngang của đồ thị hàm số.

Do đó để đồ thị hàm số có tiệm cận ngang mà không có tiệm cận đứng thì

phương trình x² - 4x + m = 0 vô nghiệm ⇔ Δ' < 0 ⇔ 4 - m < 0 ⇔ m > 4

Cách giải bài tập về tiệm cận của hàm số

A. Phương pháp giải & Ví dụ

Ví dụ minh họa

Ví dụ 1: Tìm m để đồ thị hàm số 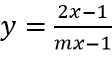có đường tiệm cận ngang cắt đường thẳng d:y = x tại điểm A(1; 1).

Hướng dẫn

Nghiệm của tử thức 2x - 1 = 0 ⇔ x = 1/2.

Để đồ thị hàm số có tiệm cận thì x = 1/2 không là nghiệm của mẫu hay m.1/2 - 1 ≠ 0 ⇔ m ≠ 2

Đường tiệm cận ngang y = 2/m

Phương trình hoành độ giao điểm của đường tiệm cận ngang y = 2/m và đường thẳng d:y = x là:

2/m = x

Mà hai đường này cắt nhau tại điểm A(1; 1) nên ta có 2/m = 1 ⇔ m = 2 (loại)

Vậy không tồn tại giá trị của m thỏa mãn yêu cầu bài toán.

Ví dụ 2: Tìm trên đồ thị hàm số 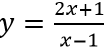những điểm M sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị

Hướng dẫn

Gọi M(a;(2a + 1)/(a - 1)) với a ≠ 1 là điểm thuộc đồ thị.

Đường tiệm cận đứng d₁: x = 1; đường tiệm cận ngang d₂:y = 2

Vì M cách đều hai tiệm cận của đồ thị hàm số nên

Với a = -2 thì tọa độ điểm M là M =(-2; 1)

Với a = 4 thì tọa độ điểm M là M =(4; 3)

Vậy các điểm cần tìm là M(-2; 1) và M(4; 3)

Ví dụ 3: Cho hàm số 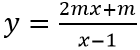) có đồ thị (C). Với giá trị nào của m thì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8.

Hướng dẫn

Để x = 1 là tiệm cận đứng của đồ thị hàm số thì x = 1 là nghiệm của mẫu nhưng không là nghiệm của tử hay 2m.1 + m ≠ 0 ⇔ 3m ≠ 0 ⇔ m ≠ 0.

Đường tiệm cận đứng x = 1; đường tiệm cận ngang y = 2m

Vì đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số cùng hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8 nên

(thỏa mãn)

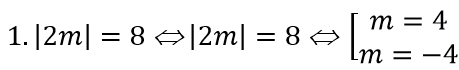
Giá trị của tham số m cần tìm là m = 4; m = -4.