Các dạng bài tập Mặt nón, mặt trụ, mặt cầu chọn lọc, có đáp án - Toán lớp 12

Các dạng bài tập Mặt nón, mặt trụ, mặt cầu chọn lọc, có đáp án

Với Các dạng bài tập Mặt nón, mặt trụ, mặt cầu chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 200 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Mặt nón, mặt trụ, mặt cầu từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Tổng hợp lý thuyết Chương Mặt nón, mặt trụ, mặt cầu

• Lý thuyết Khái niệm về mặt tròn xoay Xem chi tiết
• Lý thuyết Mặt cầu Xem chi tiết
• Lý thuyết Lý thuyết tổng hợp chương Mặt nón, mặt trụ, mặt cầu Xem chi tiết

Chủ đề: Mặt cầu

• Lý thuyết Mặt cầu ngoại tiếp, mặt cầu nội tiếp Xem chi tiết
• Dạng 1: Bài tập cơ bản về mặt cầu Xem chi tiết
• Dạng 2: Tìm tâm, bán kính mặt cầu ngoại tiếp Xem chi tiết
• Phương pháp xác định mặt cầu cực hay Xem chi tiết
• Phương pháp tính diện tích mặt cầu, thể tích khối cầu cực hay Xem chi tiết
• Phương pháp xác định mặt cầu nội tiếp, ngoại tiếp hình chóp cực hay Xem chi tiết
• Phương pháp xác định mặt cầu nội tiếp, ngoại tiếp lăng trụ cực hay Xem chi tiết

Chủ đề: Hình trụ

• Lý thuyết Mặt trụ, hình trụ Xem chi tiết
• Dạng 1: Tính chiều cao, bán kính, diện tích, thể tích hình trụ Xem chi tiết
• Dạng 2: Thiết diện của hình trụ Xem chi tiết
• Cách tính diện tích hình trụ, thể tích khối trụ cực hay Xem chi tiết
• Dạng bài tập về hình trụ, mặt trụ cực hay, có lời giải Xem chi tiết
• Dạng bài tập hình trụ nội tiếp, ngoại tiếp hình cầu, nón, lập phương cực hay Xem chi tiết

Chủ đề: Hình nón, khối nón

• Lý thuyết Khái niệm về mặt tròn xoay Xem chi tiết
• Lý thuyết Hình nón, khối nón Xem chi tiết
• Dạng 1: Tìm bán kính, đường sinh, diện tích, thể tích của hình nón Xem chi tiết
• Dạng 2: Thiết diện của hình nón Xem chi tiết
• Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón cực hay Xem chi tiết
• Cách giải dạng bài tập thiết diện của hình nón cực hay Xem chi tiết
• Dạng bài tập về hình nón tròn xoay cực hay, có lời giải Xem chi tiết

Cách xác định mặt cầu

1. Phương pháp giải

Muốn xác định tâm và bán kính của mặt cầu chúng ra cần dựa vào các tính chất sau đây:

• Tập hợp tất cả những điểm M trong không gian cách điểm O cố định một khoảng bằng R cho trước là mặt cầu tâm O bán kính R.

• Tập hợp tất cả những điểm M nhìn đoạn thẳng AB cố định dưới một góc vuông là mặt cầu đường kính AB.

• Tập hợp tất cả những điểm M sao cho tổng bình phương các khoảng cách tới hai điểm A, B cố định bằng một hằng số k² là mặt cầu có tâm là trung điểm O của đoạn AB và bán kính r = .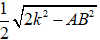

2. Ví dụ minh họa

Ví dụ 1. Cho tứ diện ABCD. Tìm tập hợp tất cả các điểm M trong không gian sao cho
|MA→ + MB→ + MC→ + MD→| = 4 .

A. Mặt nón, bán kính đáy bằng 1.

B. Mặt cầu, bán kính bằng 1.

C. Mặt trụ, bán kính bằng 1.

D. Mặt cầu, bán kính bằng 2.

Hướng dẫn giải:

+ Ta có |MA→ + MB→ + MC→ + MD→| = 4
⇔ |4MG→| = 4 ⇔ MG = 1

(với G là trọng tâm tứ diện ABCD).

+ Vậy tập hợp các điểm M trong không gian thỏa mãn là mặt cầu tâm G bán kính R= 1.

Chọn B.

Ví dụ 2. Cho tứ diện đều ABCD có cạnh bằng a. Tìm tập hợp các điểm M trong khôn gian sao cho:
MA² + MB² + MC² + MD² ≤ 2a² (*)

A. Mặt trụ, bán kính bằng .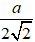

B. Mặt cầu, bán kính bằng .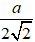

C. Khối trụ, bán kính bằng .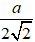

D. Khối cầu, bán kính bằng .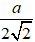

Hướng dẫn giải:

Gọi I là trung điểm của cạnh AB, J là trung điểm của CD, K là trung điểm IJ.

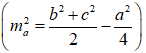
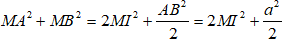
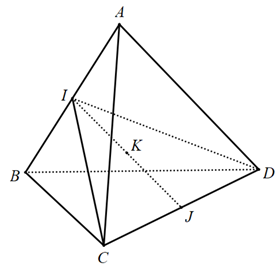
Áp dụng định lý trung tuyến trong tam giác ta có:

.

Suy ra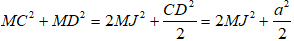

MA² + MB² + MC² + MD² = 2(MI² + MJ²) + a²
=

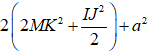
Ta có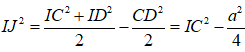
=

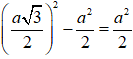
Suy ra MA² + MB² + MC² + MD² = 4MK² +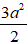

Do đó:
(*) ⇔
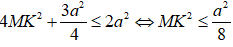
⇔ MK ≤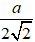

Vậy tập hợp các điểm M trong không gian là khối cầu tâm K bán kính R =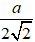

Chọn D.

Ví dụ 3. Cho mặt cầu S_{(O; R)} và điểm A cố định với OA = d. Qua A, kẻ đường thẳng Δ tiếp xúc với mặt cầu S_{(O; R)} tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?

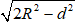
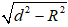
A.    B.

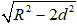
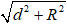
C.    D.

Hướng dẫn giải:

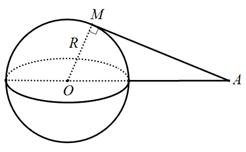
Vì Δ tiếp xúc với S_{(O; R)} tại M nên OM ⊥ Δ tại M.

Xét tam giác OMA vuông tại M, ta có:

AM² = OA² - OM² = d² - R²
⇒ AM =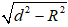

Chọn B

Cách tính diện tích hình trụ, thể tích khối trụ

1. Phương pháp giải

• Diện tích xung quanh của hình trụ là:
S_xq = 2πrh

• Diện tích toàn phần của hình trụ là:
S_tp = S_xq + S_2day = 2πrh + 2πr²

• Thể tích của khối trụ là: V = S_day.h = 2πr²h

Trong đó, r là bán kính đường tròn đáy của hình trụ.

2. Ví dụ minh họa

Ví dụ 1 Cho hình chữ nhật ABCD có AB = a và góc = 30⁰ . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:

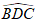
A. √3πa²    B. 2√3πa²    C. 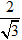πa²    D. πa²

Hướng dẫn giải:

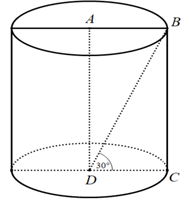
+ Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ.

Hình trụ tạo thành có:

+ Bán kính đường tròn đáy là r = AB = a

+ Đường cao của hình trụ là:
h = BC = CD.tan30⁰ =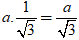

Suy ra, diện tích xung quanh của hình trụ tạo thành là:

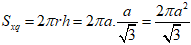
Chọn C.

Ví dụ 2 Một hình tứ diện đều ABCD cạnh a. Xét hình trụ có 1 đáy là đường tròn nội tiếp tam giác ABC và có chiều cao bằng chiều cao hình tứ diện. Diện tích xung quanh của hình trụ đó bằng:

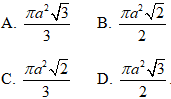
Hướng dẫn giải:

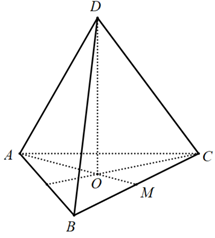
+ Gọi O là tâm của tam giác ABC và M là trung điểm BC. ( khi đó, O là trọng tâm, trực tâm, tâm đường tròn nội tiếp ( ngoại tiếp ) tam giác ABC – vì tam giác ABC đều)

+ Ta có: AM = AM.sinC = a.sin60⁰ =

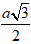
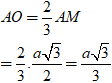
+ Chiều cao tứ diện

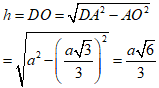
Bán kính đường tròn nội tiếp đáy ABC:
r = OM =

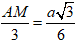
Do đó, diện tích xung quanh của hình trụ tạo thành là:

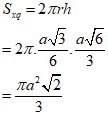
Chọn C.

Ví dụ 3 Cho hình trụ có hai đáy là hình tròn (O) và (O’). Trên hai đường tròn lấy hai điểm A, B sao cho góc giữa AB và mặt phẳng chứa đường tròn đáy bằng 45⁰ và khoảng cách đến trục OO’ bằng . Biết bán kính đáy bằng a, tính thể tích của khối trụ theo a.

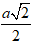
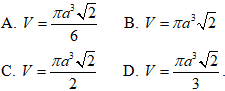
Hướng dẫn giải:

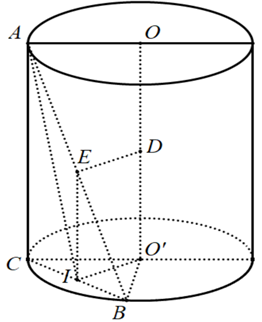
Đặt OO’ = h. Gọi I, E, D lần lượt là trung điểm của BC, BA, OO’.

Ta có: d(AB,OO') = ED = IO' =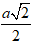

Tam giác ABC vuông tại C có B = 45⁰
⇒ tam giác ABC vuông cân

⇒ BC = AC = h

Ta có: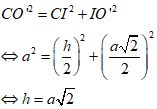

Thể tích khối trụ là: V = πa².a √2 = πa³√2

Chọn B.

Tính diện tích xung quanh, diện tích toàn phần hình nón, tính thể tích khối nón

1. Phương pháp giải

Cho hình nón (H) có bán kính đường tròn đáy là R và độ dài đường sinh là l.

+ Diện tích xung quanh của hình nón bằng nửa tích số của độ dài đường tròn đáy và độ dài đường sinh:
S_xq = πR.l

+ Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện đáy:
S_tp = πR.l + πR²

+ Thể tích khối nón bằng một phần ba tích số diện tích hình tròn đáy và chiều cao:

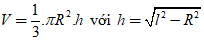
2. Ví dụ minh họa

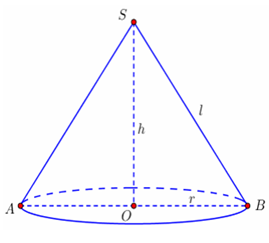
Ví dụ 1. Cho hình nón tròn xoay có đỉnh là S; O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60⁰.Tính diện tích xung quanh của hình nón và thể tích của khối nón lần lượt là?

Hướng dẫn giải:

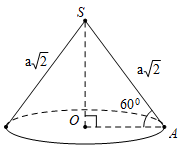
Gọi A là một điểm thuộc đường tròn đáy hình nón.

Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là
= 60⁰ .

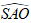
Trong tam giác vuôn SAO, ta có:

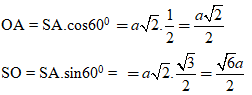
Diện tích xung quanh hình nón là:
S_xq = πRl = π.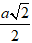 .a√2 = πR²

Thể tích của khối nón tròn xoay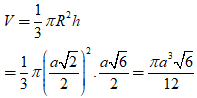
(đvtt)

Chọn A

Ví dụ 2. Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120⁰. Tính thể tích của khối nón đó theo a.

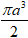
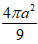
A.    B. πa³    C.    D. 2πa³

Hướng dẫn giải:

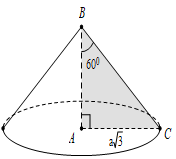
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính là:

Do góc ở đỉnh là 120⁰ nên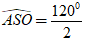

Xét tam giác SAO vuông tại O, ta có:
SO = = a

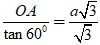
Do đó chiều cao hình nón là h = SO= a.

Vậy thể tích khối nón là
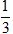
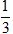
V = πr²h = π.3a².a = πa³

Chọn B.

Ví dụ 3. Một hình nón có đường sinh bằng 2a và diện tích xung quanh bằng 2πa² . Thể tích khối nón là:

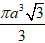
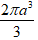
A.    B.    C. 2πa³    D. √2πa³

Hướng dẫn giải:

Ta có độ dài đường sinh là l = 2a .

Do diện tích xung quanh là 2πa² nên :

S_xq = π.R.l = 2πa² ⇒ R = = a

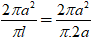
Chiều cao của hình nón là:
h = = √3a

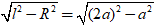
Thể tích của khối nón là
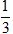
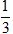
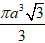
V = πR²h = π.a².√3 =

Chọn A.

Ví dụ 4. Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 3a2. Diện tích xung quanh của (N) là:

A. 6πa²    B. √2πa²    C. 6√2πa²    D. 3√2πa²

Hướng dẫn giải:

Do cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón nên thiết diện qua trục là mặt phẳng (SAB) – với AB là đường kính của đường tròn đáy.

Theo giả thiết tam giác SAB là tam giác vuông cân tại S và có diện tích 3a² nên

S_ABC = 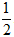SA² = 3a² ⇒ SA = √6a

Khi đó, độ dài đường sinh của hình nón là

l = SA = √6a

Do tam giác SAB là tam giác vuông cân tại S nên
AB = SA.√2 = √6a.√2 = 2√3a

Suy ra, đường cao của hình nón là:

h = SO = AB/2 = √3a

Bán kính đường tròn đáy là R = AB/2 = a√3 .

Diện tích xung quanh của (N) là:

S_xq = π.R.l = π.a√3.a.√6 = 3√2πa²

Chọn D

Ví dụ 5. Cho hình tròn có bán kính bằng 6. Cắt bỏ 1/4 hình tròn giữa hai bán kính OA và OB, rồi ghép hai bán kính đó lại sao cho hình thành một hình nón ( hình vẽ ). Tính thể tích khối nón tương ứng

Hướng dẫn giải:

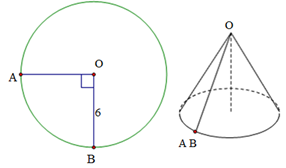
Diện tích hình tròn có bán kính bằng R = 6 là: S_tron = πR² = π6² = 36π

Cắt bỏ 1/4 hình tròn thì diện tích còn lại chính là diện tích xung quanh của nón. Đường sinh của nón là bán kính đường tròn: l = R = 6

Diện tích xung quanh của nón là:
S_xq = S_tron = .36π = 27π (1)

Lại có: S_xq = π.r.l = π.r.6 (2)

Từ (1) và (2) suy ra: π.r.6 = 27π ⇒ r =

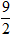
Khi đó, đường cao hình nón là:

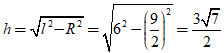
Thể tích khối nón tương ứng là:

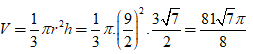
Chọn A.