Top 50 bài tập Mặt cầu (mới nhất)
Haylamdo biên soạn và sưu tầm 50 bài tập Mặt cầu Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Bài tập Mặt cầu
Câu 1:
Cho mặt cầu tâm O bán kính R và điểm A bất kì trong không gian. Điểm A không nằm ngoài mặt cầu khi và chỉ khi:
A. OA = R
B. OA ≤ R
C. OA < R
D. OA > R
Câu 2:
Cho hình chóp S.ABC có đáy là tam giác vuông cân đỉnh B và BC = a, SA ⊥ (ABC), SA = 2a. Khẳng định nào sau đây là đúng?
A. Điểm S nằm trong mặt cầu tâm A bán kính a
B. Điểm S nằm ngoài mặt cầu tâm A bán kính 2a
C. Điểm C nằm trong mặt cầu tâm A bán kính 2a
D. Cả ba điểm S, B, C cùng nằm trong mặt cầu tâm A bán kính 2a
Câu 3:
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
A. h ≤ R
B. h ≥ R
C. h > R
D. h < R
Câu 4:
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) theo a là:
A. 2a
B. a
C. a/2
D. 2a/5
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2AD = 2a. SA vuông góc với đáy, góc giữa cạnh bên SB và đáy là 45o. Bán kính mặt cầu tâm A cắt mặt phẳng (SBD) theo một đường tròn có bán kính bằng a là:
A.
B.
C.
D.
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = 2a. Bán kính mặt cầu tâm A tiếp xúc với SC theo a là:
A.
B.
C.
D.
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính mặt cầu tâm B cắt SC theo một dây có độ dài 2a là:
A.
B.
C.
D.
Câu 9:
Cho hai quả cầu cùng bán kính là 5cm. Để đựng hai quả cầu Nam phải làm một hình hộp chữ nhật từ bìa carton. Hỏi trong các đáp án dưới đây, Nam cần ít nhất bao nhiêu xen-ti-mét vuông bìa carton để làm được chiếc hộp đó?
A. 300(c)
B. 1000(c)
C. 250(c)
D. 1250(c)
Câu 10:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình chóp có mặt cầu ngoại tiếp khi và chỉ khi hình chóp có đáy là một tứ giác nội tiếp được đường tròn.
B. Hình chóp có mặt cầu ngoại tiếp nếu nó là hình chóp tam giác.
C. Hình chóp có mặt cầu ngoại tiếp nếu nó có các cạnh bên bằng nhau.
D. Hình chóp có mặt cầu ngoại tiếp nếu có cạnh bên vuông góc với đáy.
Câu 11:
Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình lăng trụ có mặt cầu ngoại tiếp nếu đáy của nó là hình vuông
B. Hình lăng trụ có mặt cầu ngoại tiếp nếu nó là lăng trụ đứng
C. Hình lăng trụ có mặt cầu ngoại tiếp nếu nó có đáy là đa giác nội tiếp được đường tròn
D. Hình lăng trụ có mặt cầu ngoại tiếp nếu nó là lăng trụ đứng tam giác
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, SA vuông góc với đáy và SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
A. a
B.
C.
D.
Câu 13:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
A. a
B.
C.
D.
Câu 14:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
A.
B.
C.
D.
Câu 15:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S,ABC, biết các cạnh đáy có độ dài bằng a , cạnh bên SA = a.
A.
B.
C.
D.
Câu 16:
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
A.
B.
C.
D.
Câu 17:
Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng:
A. 4π(c)
B. 16π/3(c)
C. 16π(c)
D. 64π(c)
Câu 18:
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) và mặt cầu (S) có điểm chung nếu và chỉ nếu:
A. h < R
B. h = R
C. h ≤ R
D. h ≥ R
Câu 19:
Trong không gian cho đường thẳng Δ và điểm O cách Δ một khoảng bằng 20cm. Mặt cầu (S) tâm O cắt đường thẳng Δ theo một dây có độ dài 30cm có bán kính r bằng:
A. r = 45cm
B. r = 30cm
C. r = 25cm
D. r = 20cm
Câu 20:
Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
A. Không điểm nào
B. Chỉ điểm S
C. Chỉ hai điểm B và C
D. Cả ba điểm
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, DSAB là tam giác đều. Bán kính mặt cầu tâm A cắt SB theo một dây có độ dài a là:
A. a/2
B. 2a
C. 2a
D. a
Câu 22:
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
A.
B.
C.
D.
Câu 23:
Cho tam giác ABC vuông tại A có BC = 2a và = 30°. Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi là diện tích toàn phần của hình nón đó và là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số ![]() là:
là:
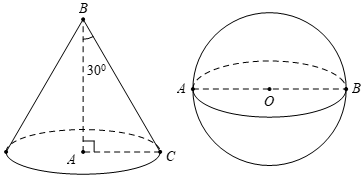
A.
B.
C.
D.
Câu 25:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB = 2AD = 2a, SA vuông góc với đáy, SA = a. Bán kính mặt cầu ngoại tiếp hình chóp là:
A.
B.
C.
D.
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA = a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A.
B.
C.
D.
Câu 27:
Cho hình chóp tứ giác đều S.ABCD có góc giữa SA và đáy là 60o, SA = 2a. Bán kính mặt cầu ngoại tiếp hình chóp là:
A.
B.
C.
D.
Câu 28:
Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:
A.
B.
C.
D.
Câu 29:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, BC = a và góc giữa A’B và mặt phẳng (ABC) là 60o. Bán kính của mặt cầu ngoại tiếp lăng trụ là:
A. 2a
B.
C.
D.
Câu 30:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD theo a.
A.
B.
C.
D.
Câu 31:
Tính bán kính của mặt cầu ngoại tiếp hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 2a.
A.
B.
C.
D.
Câu 32:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a, SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là:
A. a
B.
C.
D.
Câu 2:
Cho mặt cầu (S ) tâm O, bán kính R và mặt phẳng (P), gọi H là hình chiếu của O trên (P). Nếu thì:
A. (P) cắt (S)
B. (P) tiếp xúc (S)
C. (P) và (S) không có điểm chung
D. (P) cắt (S) tại hai điểm phân biệt
Câu 3:
Cho mặt cầu (S) và mặt phẳng (P) cắt nhau tại nhiều hơn một điểm. Giao tuyến của chúng là:
A. Mặt phẳng
B. Đường tròn
C. Đoạn thẳng
D. Hình tròn
Câu 4:
Cho mặt cầu (S) có tâm O bán kính R và đường thẳng d. Nếu d và (S) không có điểm chung thì:
A.
B.
C.
D.
Câu 8:
Mặt cầu ngoại tiếp hình đa diện nếu nó:
A. Đi qua các đỉnh của đa diện
B. Tiếp xúc với các mặt của đa diện
C. Tiếp xúc với các cạnh của đa diện
D. Đi qua trung điểm các cạnh của đa diện
Câu 9:
Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:
A. Đỉnh đa giác đáy
B. Trực tâm đa giác đáy
C. Trọng tâm đa giác đáy
D. Tâm đường tròn đáy
Câu 10:
Hình chóp tứ giác đều có trục đa giác đáy là đường thẳng
A. Đi qua tâm đáy
B. Đi qua đỉnh
C. Đi qua đỉnh và song song đáy
D. Đi qua đỉnh và tâm đáy
Câu 11:
Hình nào sau đây không có mặt cầu ngoại tiếp?
A. Hình hộp chữ nhật
B. Hình lập phương
C. Hình lăng trụ đứng có đáy là tam giác đều
D. Hình chóp có đáy là hình thoi
Câu 13:
Hình chóp nào sau đây luôn nội tiếp được mặt cầu?
A. Hình chóp tam giác
B. Hình chóp tứ giác
C. Hình chóp ngũ giác
D. Hình chóp lục giác
Câu 15:
Tâm mặt cầu ngoại tiếp hình chóp tam giác đều nằm ở đâu?
A. Trung điểm đoạn nối đỉnh với tâm đáy
B. Tâm đáy
C. Điểm nằm trên đoạn nối đỉnh với tâm đáy
D. Đỉnh hình chóp
Câu 1:
Chọn mệnh đề đúng:
A. Điểm thuộc mặt cầu thì thuộc khối cầu.
B. Điểm thuộc khối cầu thì thuộc mặt cầu.
C. Điểm nằm ngoài mặt càu thì thuộc khối cầu.
D. Điểm nằm ngoài khối cầu thì thuộc mặt cầu.
Câu 2:
Cho mặt cầu (S). Nếu (P) là mặt phẳng kính của mặt cầu (S) thì:
A. (P) tiếp xúc (S)
B. (P) không cắt (S)
C. (P) không đi qua tâm mặt cầu
D. (P) đi qua tâm mặt cầu
Câu 3:
Các tiếp tuyến tại cùng một điểm nằm trên mặt cầu có tính chất:
A. Trùng nhau
B. Song song
C. Cùng thuộc mặt phẳng
D. Vuông góc với nhau
Câu 4:
Cho mặt cầu (S) và điểm , (P) là tiếp diện của (S) tại A. Chọn mệnh đề sai:
A. Mọi đường thẳng đi qua A nằm trong (P) đều là tiếp tuyến của (S)
B. Mọi đường thẳng nằm trong (P) đều tiếp xúc với (S)
C. Các đường thẳng nằm trong (P) không thể có với (S) hai điểm chung
D. Đường thẳng OA vuông góc với (P) tại A
Câu 5:
Cho mặt cầu (S) và điểm A nằm ngoài mặt cầu, các điểm B, C, D, E lần lượt là các tiếp điểm của các tiếp tuyến kẻ từ A đến mặt cầu. Chọn mệnh đề đúng:
A. Bốn điểm B, C, D, E thẳng hàng
B. Bốn điểm B, C, D, E cùng thuộc một đường tròn
C. Bốn điểm B, C, D, E là bốn đỉnh của một hình chữ nhật
D. Bốn điểm B, C, D, E là bốn đỉnh của một hình vuông
Câu 6:
Cho mặt cầu (S) cố định và điểm A di chuyển trong không gian, vị trí của A để tập hợp các tiếp điểm của tiếp tuyến với mặt cầu kẻ từ A là đường tròn lớn là:
A. OA = R
B. Không có A
C. OA = 2R
D. OA = 0
Câu 7:
Cho mặt cầu (S) có đường kính 10 cm và mặt phẳng (P) cách tâm mặt cầu một khoảng 4 cm. Khẳng định nào sau đây sai?
A. (P) và (S) có vô số điểm chung
B. (P) và (S) theo một đường tròn bán kính 3 cm
C. (P) tiếp xúc với (S)
D. (P) cắt (S)
Câu 8:
Cho mặt cầu S(I;R) và mặt phẳng (P) cách l một khoảng bằng . Khi đó giao của (P) và (S) là đường tròn có chu vi bằng:
A.
B.
C.
D.
Câu 9:
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên b. Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:
A.
B.
C.
D.
Câu 10:
Cho hình chóp tam giác S.ABC có . Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
A. SA
B. SC
C. SC
D. AC
Câu 11:
Ba đoạn thẳng SA, SB, SC đôi một vuông góc tạo với nhau thành một tứ diện SABC với . Tính bán kính mặt cầu ngoại tiếp hình tứ diện đó là:
A.
B.
C.
D.
Câu 12:
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A có SA vuông góc với mặt phẳng (ABC) và có . Mặt cầu đi qua các đỉnh A, B, C, S có bán kính R bằng:
A.
B.
C.
D.
Câu 13:
Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là 2; 2; 1. Tính bán kính R của mặt cầu ngoại tiếp hình hộp chữ nhật trên.
A. R = 3
B.
C.
D. R = 9
Câu 14:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có . Thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’ là:
A.
B.
C.
D.
Câu 15:
Cho một mặt cầu bán kính bằng 2. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
A.
B.
C.
D.
Câu 1:
Cho hai khối cầu có bán kính lần lượt bằng a và 2a. Tỉ số thể tích của khối cầu nhỏ với thể tích của khối cầu lớn bằng
A.
B. 4
C.
D. 8
Câu 2:
Cho mặt cầu (S). Biết rằng khi cắt mặt cầu (S) bởi một mặt phẳng cách tâm một khoảng có độ dài là 3 thì được giao tuyến là đường tròn (T) có chu vi là . Diện tích của mặt cầu (S) bằng:
A.
B.
C.
D.
Câu 3:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, , đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng:
A.
B.
C.
D.
Câu 4:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, . Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B và C. Biết rằng thể tích khối chóp S.ABC bằng . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.
B.
C.
D.
Câu 5:
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân đỉnh A, . Diện tích mặt cầu ngoại tiếp tứ diện CA’B’C’ là:
A.
B.
C.
D.
Câu 6:
Cho ba hình cầu có bán kính lần lượt là đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng
A.
B.
C.
D.
Câu 7:
Cho hình chóp S.ABC có . Gọi B’, C’ lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính bán kính mặt cầu ngoại tiếp khối chóp A.BCC’B’ theo b, c,
A.
B.
C.
D.
Câu 8:
Cho hình chóp có . Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu ngoại tiếp chóp ABCNM
A.
B.
C.
D. R = 1
Câu 9:
Cho tứ diện đều ABCD có cạnh a. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
A.
B.
C.
D.
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, và . Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD
A.
B.
C.
D.
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
A.
B.
C.
D.
Câu 12:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. SA vuông góc với mặt phẳng (ABC) và . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là:
S.
B.
C.
D.
Câu 13:
Cho hình chóp đều n cạnh . Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là R và góc giữa mặt bên và mặt đáy bằng , thể tích khối chóp bằng . Tìm n?
A. n = 4
B. n = 8
C. n = 10
D. n = 6
Câu 14:
Cho hai khối cầu có cùng bán kính 2 thỏa mãn tính chất: tâm của thuộc và ngược lại. Tính thể tích phần chung V của hai khối cầu tạo bởi và
A.
B.
C.
D.
Câu 15:
Một thùng rượu vang có dạng hình tròn xoay có hai đáy là hai hình tròn bằng nhau, khoảng cách giữa hai đáy bằng 80 (cm). Đường sinh của mặt xung quanh thùng là một phần đường tròn có bán kính 60 (cm). Hỏi thùng đó có thể đựng bao nhiêu lít rượu? (làm tròn đến hàng đơn vị)
A. 771
B. 700
C. 710
D. 777
Câu 8:
Chọn mệnh đề đúng:
A. Mọi đường tròn lớn của một mặt cầu đều có chung tâm.
B. Mọi mặt phẳng kính của mặt cầu đều cùng đi qua một đường kính.
C. Mọi đường tròn lớn của một mặt cầu đều có bán kính nhỏ hơn bán kính mặt cầu.
D. Cả A, B, C đều đúng .
Câu 9:
Cho một mặt cầu bán kính bằng 1. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích hỏ nhất của chúng bằng bao nhiêu?
A.
B.
C.
D.
Câu 10:
Cho mặt cầu có bán kính , mặt cầu có bán kính . Tính tỉ số diện tích của mặt cầu và
A. 4
B. 1
C. 3
D. 2
Câu 11:
Nếu tăng bán kính của mặt cầu lên 4 lần thì diện tích mặt cầu tăng lên bao nhiêu lần?
A. 16
B. 8
C. 4
D. 64
Câu 12:
Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABD.
A.
B.
C.
D.
Câu 13:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA vuông góc với (ABCD), . Gọi E là trung điểm của AD. Bán kính mặt cầu đi qua các điểm S, A, B, C, E bằng:
A.
B.
C.
D. a
Câu 14:
Cho tứ diện ABCD có . Gọi M, N là trung điểm của AB, CD. Góc giữa hai mặt phẳng (ABD); (ABC) là . Tính biết mặt cầu đường kính MN tiếp xúc với cạnh AD.
A.
B.
C.
D.
Câu 15:
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B có cạnh AB = 3, BC = 4 và góc giữa DC và mặt phẳng (ABC) bằng . Tính thể tích mặt cầu ngoại tiếp tứ diện
A.
B.
C.
D.
Câu 16:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh . Cạnh bên SA vuông góc với mặt phẳng đáy và . Mặt phẳng qua A và vuông góc với SC cắt cạnh SB, SC, SD lần lượt tại M, N, P. Thể tích V của khối cầu ngoại tiếp tứ diện CMNP
A.
B.
C.
D.
Câu 17:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có . Gọi M là trung điểm BB’. Bán kính mặt cầu ngoại tiếp khối chóp M.A’B’C’ bằng:
A.
B.
C.
D.
Câu 18:
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho và khoảng cách từ O đến mặt phẳng (ABC) bằng 1. Thể tích của khối cầu (S) bằng:
A.
B.
C.
D.
Câu 19:
Cho lăng trụ đứng ABC.A’B’C’ có chiều cao bằng 4, đáy ABC là tam giác cân tại A với . Tính mặt cầu ngoại tiếp lăng trụ trên
A.
B.
C.
D.
Câu 20:
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, SA vuông góc với mặt phẳng (ABC), SA = 5, AB = 3, BC = 4. Bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC bằng:
A.
B.
C. 5
D.
Câu 1:
Cho đường tròn (C) đường kính AB và đường thẳng . Để hình tròn xoay sinh bởi (C) khi quay quanh là một mặt cầu thì cần có thêm điều kiện nào sau đây:
(I) Đường kính AB thuộc .
(II) cố định và đường kính AB thuộc .
(III) cố định và hai điểm A, B cố định trên .
Câu 2:
Câu 3:
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:
A.
B.
C.
D.
Câu 4:
A.
B.
C.
D.
Câu 5:
A.
B.
C.
D.
Câu 6:
A. 1,2 cm
B. 1,3 cm
C. 1 cm
D. 1,4 cm
Câu 7:
A.
B.
C.
D.
Câu 8:
A. 1,6m
B. 1,5m
C. 1,4m
D. 1,7m
Câu 9:
Cho mặt cầu S(O;R), A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60o . Diện tích của đường tròn giao tuyến bằng:
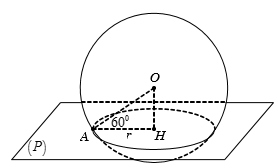
A.
B.
C.
D.
Câu 10:
A.
B.
C.
D.
Câu 11:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.
B.
C.
D.
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD ta được:
A.
B.
C.
D.
Câu 13:
A.
B.
C.
D.
Câu 14:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng . Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số bằng:
A.
B.
C.
D.
Câu 15:
A.
B.
C.
D.
Câu 16:
A.
B. a
C. 1
D.
Câu 17:
A.
B.
C.
D.
Câu 18:
A.
B. a
C.
D.
Câu 19:
A.
B. a
C.
D.
Câu 20:
A.
B.
C.
D.
Câu 21:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?
A.
B.
C.
D. a
Câu 22:
A.
B.
C.
D.
Câu 23:
A.
B.
C.
D.
Câu 24:
Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
A.
B.
C.
D.
Câu 25:
Cho tứ diện O.ABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, OB = 2a, OC = 3a. Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là:
A.
B.
C.
D.
Câu 26:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc 60o . Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số bằng ?
A.
B.
C.
D.
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Cạnh bên và vuông góc với đáy (ABCD). Bán kính mặt cầu ngoại tiếp khối chóp S.ACD nhận giá trị:
A.
B.
C.
D.
Câu 28:
A.
B.
C. a
D. 2a
Câu 29:
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, , . Góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60o . Bán kính mặt cầu ngoại tiếp tứ diện A'.ABC bằng:
A.
B.
C.
D.
Câu 30:
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60o và điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A'B'C' bằng:
A.
B.
C.
D.
Câu 31:
Câu 35:
Cho hai mặt cầu (S) và (S’) lần lượt có tâm I và J, bán kính R và R’. Đặt d = IJ. Câu nào sau đây sai?
I. và (S') trong nhau
II. và (S') ngoài nhau
III. và (S') tiếp xúc ngoài
IV. và (S') tiếp xúc trongCâu 36:
A.
B.
C.
D. Hai câu A và B
Câu 37:
Cho mặt cầu và mặt phẳng
I. cắt (S)
II. tiếp xúc (S)
III. không cắt (S)Câu 38:
A.
B.
C.
D.
Câu 41:
Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu:
A.
B.
C.
D.
Câu 42:
Tìm tập hợp các tâm I của mặt cầu
Câu 45:
Mặt phẳng và mặt cầu
Câu 46:
Câu 49:
A.
B.
C.
D.
Câu 50:
A.
B.
C.
D.
Câu 51:
A.
B.
C.
D. Hai câu A và C
Câu 52:
A.
B.
C.
D.
Câu 53:
Cho mặt cầu . Viết phương trình tổng quát của đường kính AB song song với đường thẳng
A.
B.
C.
D.
Câu 54:
A.
B.
C.
D.
Câu 55:
B.
C.
D.
Câu 56:
Cho mặt cầu . Gọi A là giao điểm của (S) và trục y'Oy có tung độ âm. Viết phương trình tổng quát của tiếp diện (Q) của (S) tại A
A.
B.
C.
D.
Câu 57:
A.
B.
C.
D.
Câu 59:
A.
B. m = 12
C. m = 6
D. m = 18
Câu 60:
A.
B. 1
C. 7
D.
Câu 63:
A.
B.
C.
D.
Câu 64:
A.
B.
C.
D.
Câu 65:
A.
B.
C.
D.
Câu 66:
A.
B.
C.
D.
Câu 67:
Viết phươngng trình mặt cầu (S) tâm I(4,2,-1) nhận đường thẳng (D): làm tiếp tuyến.
A.
B.
C.
D.
Câu 69:
A.
B.
C.
D.
Câu 70:
A.
B.
C.
D.
Câu 71:
Câu 72:
A.
B.
C.
D.
Câu 73:
A.
B.
C.
D.
Câu 74:
A.
B.
C.
D.
Câu 76:
Viết phương trình mặt cầu (S) qua ba điểm A(2,0,1); B(1,3,2); C(3,2,0) có tâm nằm trong mặt phẳng (xOy)
A.
B.
C.
D.
Câu 77:
A.
B.
C.
D.
Câu 78:
A.
B.
C.
D.
Câu 79:
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có trùng với ba trục . Viết phương trình mặt cầu ( S3 ) tiếp xúc với tất cả các cạnh của hình lập phương.
A.
B.
C.
D.
Câu 80:
A. 10
B. 8
C. 4
D. 6
Câu 81:
Cho hai điểm A(2,-3,-2); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) sao cho
Câu 82:
Cho hai điểm A(2,-3,-1); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
Câu 83:
Cho hai điểm A(2,-3,-1); B()-4,5,-3. Tìm tập hợp các điểm M(x, y, z) thỏa mãn
Câu 84:
A.
B.
C.
D.
Câu 85:
Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn
Câu 86:
Cho tứ diện OABC với A(-4,0,0); B(0,6,0); C(0,0,-8). Mặt cầu (S) ngoại tiếp từ diện có tâm và bán kính là:
A.
B.
C.
D.
Câu 87:
Câu 88:
Tìm tập hợp các tâm I của mặt cầu
Câu 89:
Tìm tập hợp các tâm I của mặt cầu (S): ,
Câu 90:
Câu 91:
Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng
Câu 92:
Câu 93:
Câu 94:
Câu 95:
Câu 96:
A. 10
B. 8
C. 6
D. 4
Câu 97:
Câu 98:
Cho mặt cầu (S): và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tìm tập hợp các điểm M.
Câu 99:
A.
B.
C.
D.
Câu 100:
A.
B.
C.
D.
Câu 101:
Cho tứ diện ABCD có A(3, 6, -2); B(6, 0, 1); C(-1, 2, 0); D(0, 4, 1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ :
A. I(3, -2, 1)
B. (3, 2, -1)
C. I(-3, 2, 1)
D. I(3, -2, -1)
Câu 102:
A.
B.
C.
D.
Câu 104:
Trong không gian cho đường tròn . Bán kính r của đường tròn (C) bằng :
A.
B.
C.
D.
Câu 106:
A.
B.
C.
D.
Câu 107:
Trong không gian Oxyz cho đường tròn . Bán kính r của đường tròn (C) bằng :
A.
B.
C.
D.
Câu 108:
Trong không gian Oxyz cho đường tròn (C) có tâm H và bán kính r bằng:
A.
B.
C.
D.
Câu 109:
Cho mặt cầu và ba điểm A(1,2,-2); B(-4,2,3); C(1,-3,3) nằm trên mặt cầu (S). Bán kính r của đường tròn ngoại tiếp tam giác ABC là :
A.
B.
C.
D.