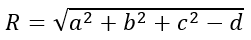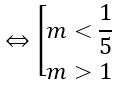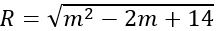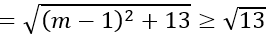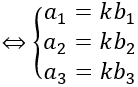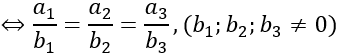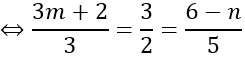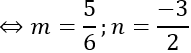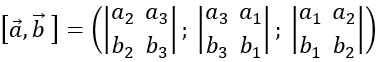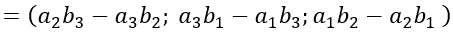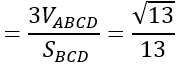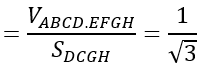Các dạng bài tập Phương pháp tọa độ trong không gian chọn lọc, có đáp án - Toán lớp 12
Các dạng bài tập Phương pháp tọa độ trong không gian chọn lọc, có đáp án
Với Các dạng bài tập Phương pháp tọa độ trong không gian chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 200 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương pháp tọa độ trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

Tổng hợp lý thuyết Chương Phương pháp tọa độ trong không gian
- Lý thuyết Hệ tọa độ trong không gian Xem chi tiết
- Lý thuyết Phương trình mặt phẳng Xem chi tiết
- Lý thuyết Phương trình đường thẳng trong không gian Xem chi tiết
- Lý thuyết tổng hợp chương Phương pháp tọa độ trong không gian Xem chi tiết
Chủ đề: Hệ tọa độ trong không gian
- 4 dạng bài tập về Hệ tọa độ trong không gian trong đề thi Đại học có lời giải Xem chi tiết
- Dạng 1: Tìm tọa độ của vecto, của điểm Xem chi tiết
- Dạng 2: Tích vô hướng của hai vecto trong không gian Xem chi tiết
- Dạng 3: Chứng minh hai vecto cùng phương, không cùng phương Xem chi tiết
- Dạng 4: Tích có hướng của hai vecto trong không gian Xem chi tiết
Chủ đề: Phương trình mặt cầu
- 4 dạng bài tập Viết phương trình mặt cầu trong đề thi Đại học có lời giải Xem chi tiết
- Dạng 1: Tìm tâm và bán kính mặt cầu Xem chi tiết
- Dạng 2: Viết phương trình mặt cầu Xem chi tiết
- Dạng 2.1: Viết phương trình mặt cầu có tâm I Xem chi tiết
- Dạng 2.1.1: Viết phương trình mặt cầu biết tâm I (a; b; c) và bán kính R Xem chi tiết
- Dạng bài 2.1.2: Viết phương trình mặt cầu biết tâm I (a; b; c) và mặt cầu tiếp xúc với mặt phẳng (P): Ax + By + Cz + D = 0 Xem chi tiết
- Dạng bài 2.1.3: Viết phương trình mặt cầu biết tâm I (a; b; c) và tiếp xúc với đường thẳng Xem chi tiết
- Dạng bài 2.1.4: Viết phương trình mặt cầu biết I (a; b; c) và mặt cầu cắt mặt phẳng (P): Ax + By + Cz + D = 0 theo một đường tròn có bán kính r Xem chi tiết
- Dạng bài 2.1.5: Viết phương trình mặt cầu biết I (a; b; c) và mặt cầu cắt đường thẳng Δ theo một dây cung có độ dài l cho trước Xem chi tiết
- Dạng 2.2: Viết phương trình mặt cầu có tâm I thuộc đường đẳng d Xem chi tiết
- Dạng 2.2.1: Viết phương trình mặt cầu có tâm thuộc đường thẳng d và đi qua 2 điểm A, B Xem chi tiết
- Dạng 2.2.2: Mặt cầu có tâm thuộc d, cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính r và tâm I cách mặt phẳng (P) một khoảng h Xem chi tiết
- Dạng 2.2.3: Mặt cầu có tâm thuộc d, cắt đường thẳng Δ theo một dây cung có độ dài l và tâm I cách đường thẳng Δ một khoảng là h Xem chi tiết
- Dạng 2.2.4: Mặt cầu có tâm thuộc d, tiếp xúc với mặt phẳng (P) và thỏa mãn một điều kiện cho trước Xem chi tiết
- Dạng 2.3: Viết phương trình mặt cầu tiếp xúc với mặt phẳng P Xem chi tiết
- Dạng 2.4: Viết phương trình mặt cầu tiếp ngoại tiếp tứ diện Xem chi tiết
- Dạng 2.5: Viết phương trình mặt cầu đi qua 3 điểm Xem chi tiết
- 60 bài tập trắc nghiệm Viết phương trình mặt cầu chọn lọc, có đáp án Xem chi tiết
Chủ đề: Phương trình mặt phẳng
- 21 dạng bài tập Viết phương trình mặt phẳng trong đề thi Đại học có lời giải Xem chi tiết
- Dạng 1: Viết phương trình mặt phẳng đi qua 1 điểm và có vecto pháp tuyến Xem chi tiết
- Dạng 2: Viết phương trình mặt phẳng đi qua 1 điểm và song song với mặt phẳng Xem chi tiết
- Dạng 3: Viết phương trình mặt phẳng đi qua 3 điểm Xem chi tiết
- Dạng 4: Viết phương trình mặt phẳng đi qua 1 điểm và vuông góc với đường thẳng Xem chi tiết
- Dạng 5: Viết phương trình mặt phẳng chứa đường thẳng và vuông góc với mặt phẳng Xem chi tiết
- Dạng 6: Viết phương trình mặt phẳng chứa đường thẳng và song song với đường thẳng Xem chi tiết
- Dạng 7: Viết phương trình mặt phẳng chứa đường thẳng và điểm Xem chi tiết
- Dạng 8: Viết phương trình mặt phẳng chứa 2 đường thẳng cắt nhau Xem chi tiết
- Dạng 9: Viết phương trình mặt phẳng chứa 2 đường thẳng song song Xem chi tiết
- Dạng 10: Viết phương trình mặt phẳng đi qua 1 điểm và song song với hai đường thẳng chéo nhau Xem chi tiết
- Dạng 11: Viết phương trình mặt phẳng đi qua 1 điểm và vuông góc với 2 mặt phẳng Xem chi tiết
- Dạng 12: Viết phương trình mặt phẳng P song song và cách mặt phẳng Q một khoảng k Xem chi tiết
- Dạng 13: Viết phương trình mặt phẳng P song song với mặt phẳng Q và cách điểm M một khoảng k Xem chi tiết
- Dạng 14: Viết phương trình mặt phẳng tiếp xúc hoặc cắt mặt cầu Xem chi tiết
- Dạng 15: Viết phương trình mặt phẳng chứa đường thẳng và tạo với mặt phẳng một góc Xem chi tiết
- 50 bài tập trắc nghiệm Viết phương trình mặt phẳng chọn lọc, có đáp án Xem chi tiết
Chủ đề: Phương trình đường thẳng trong không gian
- Các công thức về đường thẳng, phương trình đường thẳng trong không gian Xem chi tiết
- 19 dạng bài tập Viết phương trình đường thẳng trong đề thi Đại học có lời giải Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và có vecto chỉ phương u Xem chi tiết
- Viết phương trình đường thẳng đi qua 2 điểm Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và vuông góc với mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và song song với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng là giao tuyến của hai mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, song song với mặt phẳng và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng nằm trong mặt phẳng, đi qua 1 điểm và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, cắt đường thẳng d và song song với mặt phẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và vuông góc với 2 đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm và cắt hai đường thẳng Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, vuông góc với đường thẳng d1 và cắt đường thẳng d2 Xem chi tiết
- Viết phương trình đường thẳng đi qua 1 điểm, cắt và vuông góc với đường thẳng Xem chi tiết
- Viết phương trình đường thẳng nằm trong mặt phẳng và cắt hai đường thẳng Xem chi tiết
- Viết phương trình đường thẳng song song với đường thẳng và cắt 2 đường thẳng Xem chi tiết
- Viết phương trình đường vuông góc chung của hai đường thẳng chéo nhau Xem chi tiết
- Viết phương trình đường thẳng là hình chiếu của đường thẳng lên mặt phẳng Xem chi tiết
- II. Vị trí tương đối của hai đường thẳng trong không gian Xem chi tiết
- III. Vị trí tương đối của đường thẳng và mặt phẳng Xem chi tiết
- IV. Vị trí tương đối của đường thẳng và mặt cầu Xem chi tiết
- V. Hình chiếu của một điểm lên đường thẳng, mặt phẳng Xem chi tiết
- Khoảng cách từ 1 điểm đến 1 đường thẳng; Khoảng cách giữa 2 đường thẳng chéo nhau Xem chi tiết
- Viết phương trình đường thẳng liên quan đến khoảng cách Xem chi tiết
- VII.Góc giữa hai đường thẳng; Góc giữa đường thẳng và mặt phẳng Xem chi tiết
- VIII.Tìm điểm thuộc đường thẳng thỏa điều kiện cho trước, bài toán về cực trị,... Xem chi tiết
- 60 câu hỏi trắc nghiệm đường thẳng trong không gian có lời giải Xem chi tiết
Bài tập trắc nghiệm
Cách tìm tâm và bán kính mặt cầu
A. Phương pháp giải & Ví dụ
+ Phương trình (S): (x-a)2+(y-b)2+(z-c)2=R2 là phương trình mặt cầu (S) có tâm I (a; b; c), bán kính R
+ Phương trình (S): x2+y2+z2-2ax-2by-2cz+d=0 thỏa mãn điều kiện a2+b2+c2-d>0 là phương trình mặt cầu tâm I (a; b; c); bán kính
Ví dụ minh họa
Bài 1: Trong không gian hệ trục tọa độ Oxyz, phương trình nào sau đây là phương trình mặt cầu, nếu là phương trình mặt cầu, hãy tìm tâm và bán kính của mặt cầu đó
a) (x-2)2+(y+3)2+z2=5
b) x2+y2+z2-2x+4y-6z+1=0
c) 3x2+3y2+3z2-6x+3y+21=0
Hướng dẫn:
a) Phương trình (x-2)2+(y+3)2+z2=5 có dạng
(x-a)2+(y-b)2+(z-c)2=R2 nên là phương trình mặt cầu có tâm
I (2; -3; 0) và bán kính R=√5.
b) Phương trình x2+y2+z2-2x+4y-6z+1=0 có dạng
x2+y2+z2-2ax-2by-2cz+d=0 với a = 1; b = -2; c = 3, d = 1
⇒ a2+b2+c2-d=13>0
Vậy phương trình đã cho là phương trình mặt cầu có tâm I (1; -2; 3) và bán kính R=√13.
c) Phương trình 3x2+3y2+3z2-6x+3y+21=0
⇔ x2+y2+z2-2x+y+7=0
Phương trình có dạng x2+y2+z2-2ax-2by-2cz+d=0 với
a=1;b=(-1)/2;c=0;d=7 ⇒a2+b2+c2-d=(-23)/4<0
Vậy phương trình đã cho không phải là phương trình mặt cầu.
Bài 2: Trong không gian với hệ tọa độ Oxyz, tìm m để mỗi phương trình sau là phương trình mặt cầu.
a) x2+y2+z2-2mx+2(m+1)y-4z+1=0
b) x2+y2+z2-2(m-3)x-4mz+8=0
Hướng dẫn:
a) Phương trình x2+y2+z2-2mx+2(m+1)y-4z+1=0 có
a=m;b=-(m+1); c=2;d=1.
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ m2+(m+1)2+22-1>0⇔2m2+2m+3>0 ⇔m∈R.
b) Phương trình x2+y2+z2-2(m-3)x-4mz+8=0 có a=m-3;
b=0;c=2m;d=8
Phương trình là phương trình mặt cầu ⇔a2+b2+c2-d>0
⇔(m-3)2+4m2-8>0 ⇔5m2-6m+1>0
Bài 3: Trong không gian hệ trục tọa độ Oxyz, tìm tất cả các giá trị thực của tham số m để phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 là phương trình của mặt cầu có bán kính nhỏ nhất.
Hướng dẫn:
Phương trình x2+y2+z2+2(m+2)x-2(m-3)z+m2-1=0 có:
a=-(m+2);b=0;c=m-3;d=m2-1
Phương trình là phương trình mặt cầu ⇔ a2+b2+c2-d>0
⇔ (m+2)2+(m-3)2-m2+1>0 ⇔ m2-2m+14>0 ⇔ m∈R.
Khi đó, bán kính mặt cầu là:
Dấu bằng xảy ra khi m = 1.
Vậy với m = 1 thì mặt cầu có bán kính nhỏ nhất R=√13.
Chứng minh hai vecto cùng phương, không cùng phương
A. Phương pháp giải & Ví dụ
a→cùng phương với b→ (b→ ≠ 0→ )⇔ a→=k b→ (k∈R)
Ví dụ minh họa
Bài 1: Trong không gian hệ tọa độ Oxyz, cho các vecto a→=(3;2;5),
b→ =(3m+2;3;6-n). Tìm m, n để a→ , b→ cùng phương,
Hướng dẫn:
Ta có: a→=(3;2;5), b→=(3m+2;3;6-n).
a→ , b→ cùng phương
Bài 2: Trong không gian hệ trục Oxyz, cho các điểm A (1; 2; 3), B(2; 1; 1), C (0; 2; 4)
a) Chứng minh A, B, C là 3 đỉnh của một tam giác.
b) Tìm tọa độ điểm M thuộc mặt phẳng Oyz sao cho 3 điểm A, B, M thẳng hàng.
Hướng dẫn:
a) Ta có: AB→=(1; -1; -2), AC→=(-1;0;1)
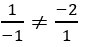
b) M∈(Oyz)⇒M(0;y;z)
AM→ =(-1;y-2;z-3), AB→=(1; -1; -2)
A, B, M thẳng hàng ⇔ AM→, AB→ cùng phương
⇔y=3;z=5
Vậy M (0; 3; 5)
Bài 3: Trong không gian với hệ toạ độ Oxyz, cho tứ giác ABCD có A(2; -1; 5), B(5; -5; 7), C(11; -1; 6), D(5; 7; 2) . Tứ giác ABCD là hình gì?
Hướng dẫn:
AB→=(3; -4;2)
DC→=(6; -8;4)
⇒ DC→=2 AB→ hay DC // AB
⇒ Tứ giác ABCD là hình thang có đáy AB và CD
Công thức tính Tích có hướng của hai vecto trong không gian
A. Phương pháp giải & Ví dụ
1. Định nghĩa:
Trong không gian Oxyz cho hai vecto a→=(a1;a2;a3 ) và b→=(b1;b2;b3 ). Tích có hướng của hai vecto a→ và b→ , kí hiệu là [a→ , b→ ], được xác định bởi
Chú ý: Tích có hướng của hai vecto là một vecto, tích vô hướng của hai vecto là một số.
2. Tính chất
+ [a→, b→ ]⊥ a→ ; [a→ , b→ ]⊥ b→
+ [a→ , b→ ]=-[b→, a→ ]
+ [i→, j→ ]=k→ ; [ j→ , k→ ]= i→ ; [k→ , i→ ]= j→
+ |[ a→ , b→ ]|=| a→ |.| b→ |.sin( a→ , b→ )
+ a→ , b→ cùng phương ⇔ [a→ , b→ ]= 0→ (chứng minh 3 điểm thẳng hàng)
3. Ứng dụng của tích có hướng (chương trình nâng cao)
+ Điều kiện đồng phẳng của ba vecto:
a→ , b→ và c→ đồng phẳng ⇔[ a→ , b→ ]. c→ =0
+ Diện tích hình bình hành ABCD:
SABCD=|[AB→ ; AD→ ]|
+ Diện tích tam giác ABC:
SABC=1/2 |[AB→ ; AC→ ]|
+ Thể tích khối hộp ABCD.A’B’C’D’:
VABCD.A'B'C'D'=|[AB→; AD→ ]. AA'→ |
+ Thể tích tứ diện ABCD
VABCD=1/3 |[AB→ ; AC→ ]. AD→ |
Ví dụ minh họa
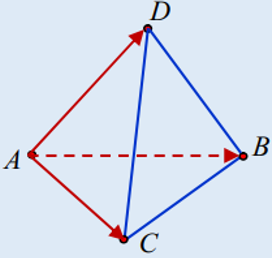
Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(1; 0; 1), B(-1; 1; 2), C(-1; 1; 0), D(2; -1; -2).
a) Chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện.
b) Tính thể tích tứ diện ABCD. Suy ra độ dài đường cao của tứ diện qua đỉnh A
Hướng dẫn:
AB→ =(-2;1;1); AC→ =(-2;1; -1); AD→ =(1; -1; -3)
⇒[AB→ , AC→ ]=(-2;-4;0) ⇒[ AB→ , AC→ ]. AD→ =2≠0
⇒AB→ , AC→ , AD→ không đồng phẳng.
Vậy A, B, C, D là 4 đỉnh của một tứ diện.
b) VABCD=1/6 |[AB→ , AC→ ]. AD→ |=2/6=1/3
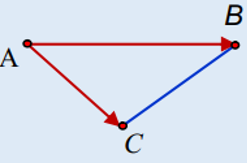
Ta có: BC→ =(0;0; -2), BD→ =(3; -2; -4)
⇒[ BC→ , BD→ ]=(-4; -6;0)⇒SBCD=1/2 |[BC→ , BD→ ]|=√13
VABCD=1/3 d(A;(BCD)).SBCD
⇒d(A;(BCD))
Bài 2: Trong không gian hệ trục tọa độ Oxyz, cho 4 điểm A(-3; 5; 15), B(0; 0; 7), C(2; -1; 4), D(4; -3; 0). Chứng minh AB và CD cắt nhau.
Hướng dẫn:
+ Ta có: AB→ =(3; -5; -8); AC→ =(5; -6; -11);
AD→ =(7; -8; -15), CD→ =(2; -2; -4)
⇒[ AB→ , AC→ ]=(7;-7;7) ⇒[ AB→ ,(AC) ⃗ ].(AD) ⃗=0
⇒ AB→ , AC→ , AD→ đồng phẳng.
⇒ A, B, C, D cùng thuộc một mặt phẳng (1)
+ [AB→ , CD→ ]=(4; -4;4) ≠0→ ⇔ AB→ , CD→ không cùng phương (2)
Từ (1) và (2) suy ra AB và CD cắt nhau.
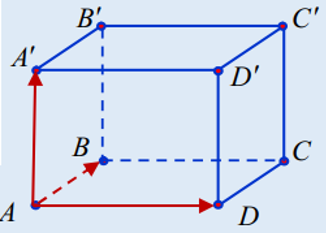
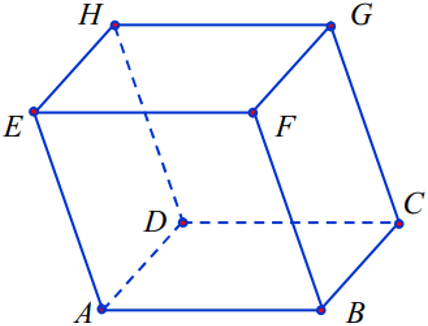
Bài 3: : Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.EFGH với A(1; 1; 1), B(2; 1; 2), E(-1; 2; -2), D(3; 1; 2). Tính khoảng cách từ A đến mặt phẳng (DCGH)
Hướng dẫn:
+ AB→=(1;0;1), AD→=(2;0;1), AE→=(-2;1; -3)
⇒[ AB→ , AD→ ]=(0;1;0)⇒[ AB→ , AD→ ]. AE→=1
⇒VABCD.EFGH=|[ AB→ , AD→ ]. AE→ |=1
+ SAEFB=|[ AB→ , AE→ ]|=√3
⇒SDCGH=SAEFB=√3
VABCD.EFGH=d(A;(DCGH)).SDCGH
⇒d(A;(DCGH))