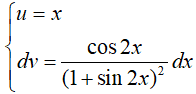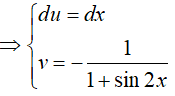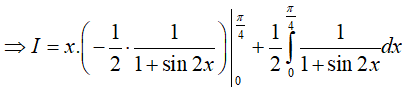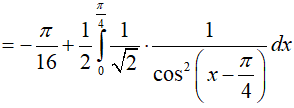Các dạng bài tập Tích phân chọn lọc, có đáp án - Toán lớp 12

---

Các dạng bài tập Tích phân chọn lọc, có đáp án

Với Các dạng bài tập Tích phân chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 300 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tích phân từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

• Công thức tích phân Xem chi tiết
• Phương pháp tính tích phân cơ bản cực hay Xem chi tiết
• Cách tính tích phân bằng phương pháp đổi biến số cực hay Xem chi tiết
• Phương pháp tính tích phân từng phần cực hay Xem chi tiết
• Phương pháp tính tích phân hàm chứa dấu giá trị tuyệt đối cực hay Xem chi tiết
• Phương pháp tính tích phân hàm số chẵn, hàm số lẻ cực hay Xem chi tiết
• 3 ứng dụng của tích phân: tính diện tích, thể tích, quãng đường, vận tốc cực hay Xem chi tiết
• Dạng 6: Tính tích phân bằng định nghĩa và tính chất Xem chi tiết
• Trắc nghiệm tính tích phân bằng định nghĩa và tính chất Xem chi tiết
• Dạng 7: Tính tích phân từng phần Xem chi tiết
• Trắc nghiệm tính tích phân từng phần Xem chi tiết
• Dạng 8: Tính tích phân bằng phương pháp đổi biến số loại 1 Xem chi tiết
• Trắc nghiệm tính tích phân bằng phương pháp đổi biến số loại 1 Xem chi tiết
• Dạng 9: Tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
• Trắc nghiệm tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
• Dạng 10: Tính tích phân hàm chứa dấu giá trị tuyệt đối Xem chi tiết
• Trắc nghiệm tính tích phân hàm chứa dấu giá trị tuyệt đối Xem chi tiết
• Dạng 11: Tính tích phân hàm số hữu tỉ Xem chi tiết
• Trắc nghiệm tính tích phân hàm số hữu tỉ Xem chi tiết
• Dạng 12: Ứng dụng của tích phân: Tính diện tích hình phẳng Xem chi tiết
• Trắc nghiệm ứng dụng của tích phân: Tính diện tích hình phẳng Xem chi tiết
• Dạng 13: Ứng dụng của tích phân: Tính thể tích khối tròn xoay Xem chi tiết
• Trắc nghiệm ứng dụng của tích phân: Tính thể tích khối tròn xoay Xem chi tiết
• Bài tập về tính chất của tích phân Xem chi tiết
• Bài tập tính tích phân cơ bản Xem chi tiết
• Tính tích phân hàm đa thức, phân thức bằng phương pháp đổi biến số Xem chi tiết
• Tính tích phân hàm lượng giác bằng phương pháp đổi biến số Xem chi tiết
• Tính tích phân hàm số mũ, logarit bằng phương pháp đổi biến số Xem chi tiết
• Tính tích phân hàm chứa căn thức bằng phương pháp đổi biến số Xem chi tiết
• Cách tính tích phân bằng phương pháp đổi biến số loại 2 Xem chi tiết
• Bài tập tính tích phân nâng cao Xem chi tiết
• Tính tích phân hàm lượng giác bằng phương pháp tích phân từng phần Xem chi tiết
• Tính tích phân hàm số mũ, logarit bằng phương pháp tích phân từng phần Xem chi tiết
• Tính tích phân của hàm số chẵn, hàm số lẻ Xem chi tiết
• Hàm số dưới dấu tích phân là thương của hàm chẵn và hàm mũ Xem chi tiết
• Tích phân của hàm trị tuyệt đối Xem chi tiết
• Bài tập tích phân nâng cao Xem chi tiết
• Ứng dụng tích phân: Tính diện tích hình phẳng Xem chi tiết
• Ứng dụng tích phân: Tính thể tích vật thể và khối tròn xoay Xem chi tiết

Bài tập trắc nghiệm

• 150 bài tập trắc nghiệm Nguyên hàm, Tích phân và ứng dụng có lời giải (cơ bản) Xem chi tiết
• 150 bài tập trắc nghiệm Nguyên hàm, Tích phân và ứng dụng có lời giải (nâng cao) Xem chi tiết

Phương pháp tính tích phân cơ bản

Dạng 1. Tính chất của tích phân

1. Phương pháp giải

Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a,b,c là ba số bất kỳ thuộc K. Khi đó ta có

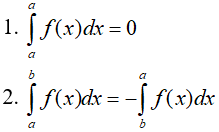
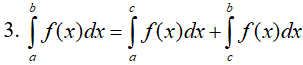
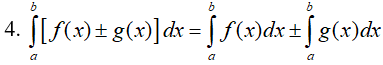
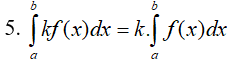
Nếu f(x) ≥ 0, ∀x ∈ [a, b] thì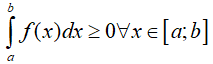

Nếu ∀x ∈ [a, b]: f(x) ≥ g(x)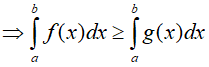

Nếu ∀x ∈ [a, b] nếu M ≤ f(x) ≤ N thì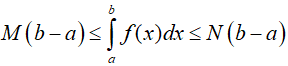

2. Ví dụ minh họa

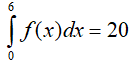
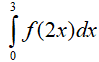
Ví dụ 1. Cho tích phân . Tính tích phân

A . I= 40    B. I= 10    C. I= 20    D. I= 5

Hướng dẫn:

Đáp án: B

Đặt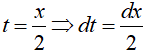

Đổi cận: với x = 0 => t = 0

Với x = 6 => t = 3

Ta có:

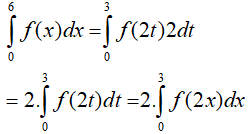
Suy ra: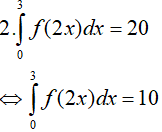

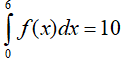
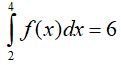
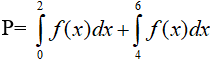
Ví dụ 2. Cho hàm số y= f(x) liên tục trên đoạn [0; 6] thỏa mãn và . Tính giá trị của biểu thức

A. P= 4    B. P= 16    C. P= 8    D. P= 10

Hướng dẫn:

Đáp án: A

Ta có:

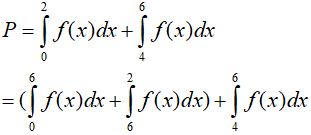
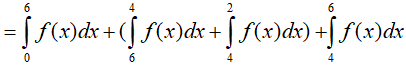
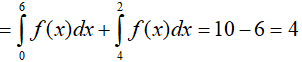
Dạng 2. Tính trực tiếp

1. Phương pháp giải

Cho hàm số y= f(x) liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì: .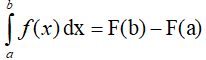

Như vậy, để tính tích phân của 1 hàm số ta cần:

• Bước 1: Xác định F(x) là nguyên hàm của hàm số.

• Bước 2. Tính F(b) − F(a).

Dạng 2.1. Hàm đa thức

2. Ví dụ minh họa

Ví dụ 1. Tích phân 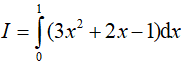bằng

A.I=1    B.I= 2    C.I= 3    D. I= −1

Hướng dẫn:

Đáp án: A

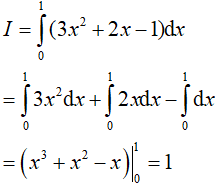
Ví dụ 2. Có bao nhiêu giá trị của m sao cho :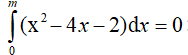

A.1    B. 2    C. 3    D. 4

Hướng dẫn:

Đáp án: A

Ta có:

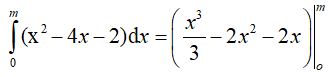
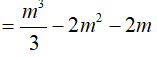
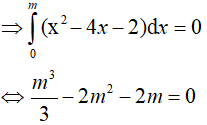
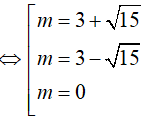
Vậy có 3 giá trị của m thỏa mãn.

Dạng 2.2. Hàm phân thức

Ví dụ minh họa

Ví dụ 1. Tích phân 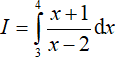bằng

Hướng dẫn:

Đáp án: D

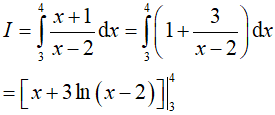
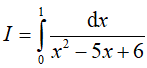
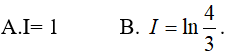
Ví dụ 2. Tích phân bằng

Hướng dẫn:

Đáp án: B

Ta có:

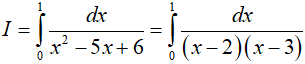
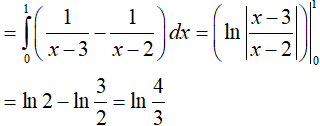
Dạng 2.3. Hàm căn thức

Ví dụ minh họa

Ví dụ 1. Tính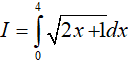

Hướng dẫn:

Đáp án: C

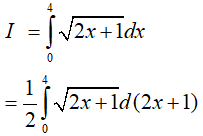
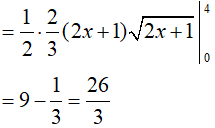
Ví dụ 2. Tính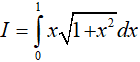

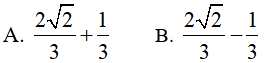
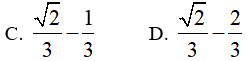
Hướng dẫn:

Đáp án: B

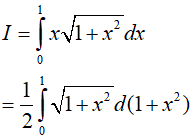
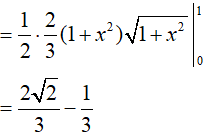
Dạng 2.4. Hàm lượng giác

2. Ví dụ minh họa

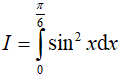
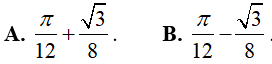
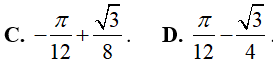
Ví dụ 1. Tích phân có giá trị là

Hướng dẫn:

Đáp án: B

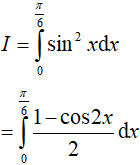
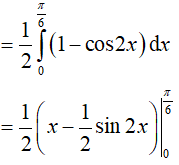
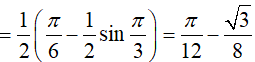
Ví dụ 2. Tích phân có giá trị là

Hướng dẫn:

Đáp án: A

Ta có

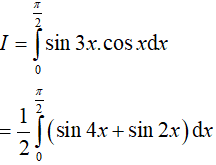
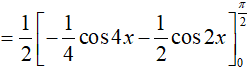
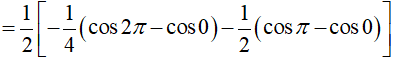
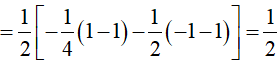
Dạng 2.5. Hàm mũ, logarit

2. Ví dụ minh họa

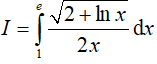
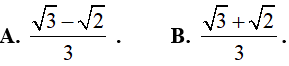
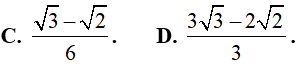
Ví dụ 1. Tích phân bằng

Hướng dẫn:

Đáp án: D

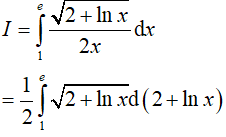
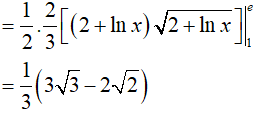
Vậy: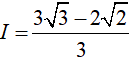

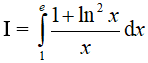
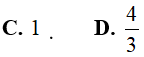
Ví dụ 2. Tích phân có giá trị là:

Hướng dẫn:

Đáp án: D

Ta có:

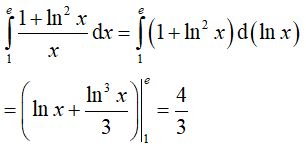
Cách tính tích phân bằng phương pháp đổi biến số

Phương pháp giải

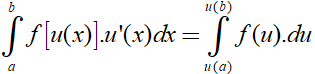
Trong đó u= u(x) có đạo hàm liên tục trên K, hàm số y= f(u) liên tục và sao cho hàm hợp f[u(x)] xác định trên K; a và b là hai số thuộc K

Dạng 3.1. Hàm đa thức

Ví dụ minh họa

Ví dụ 1. Tích phân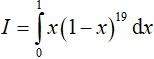

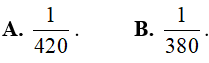
Hướng dẫn:

Đáp án: A

Đặt t = 1 − x => −dt = dx. Đổi cận: x = 0 => t = 1; x = 1 => t = 0

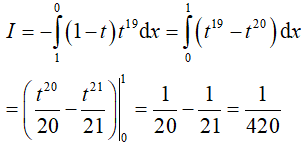
Dạng 3.2. Hàm phân thức

Ví dụ minh họa

Ví dụ 1. Tích phân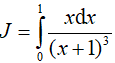

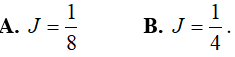
Hướng dẫn:

Đáp án: A

Đặt t = x+ 1 => dt = dx. Đổi cận: x = 0 => t = 1; x = 1 => t = 2

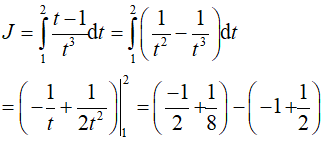
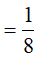
Ví dụ 2. Tích phân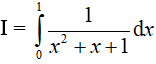

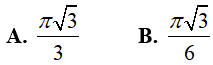
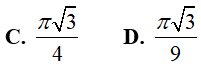
Hướng dẫn:

Đáp án: D

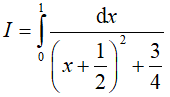
Đặt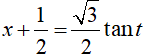

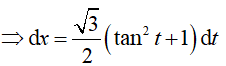
Đổi cận:

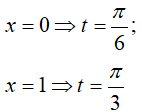
Khi đó

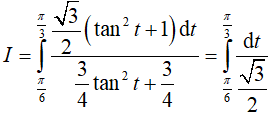
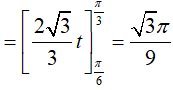
Vậy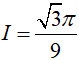

Dạng 3.3. Hàm căn thức

Ví dụ minh họa

Ví dụ 1. Tích phân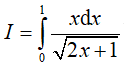

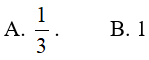
Hướng dẫn:

Đáp án: A

Đặt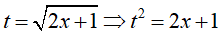

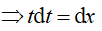
Đổi cận x = 0 => t = 1; x = 1 => t = √

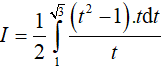
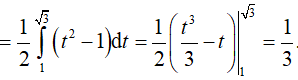
Ví dụ 2. Tính

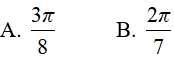
Hướng dẫn:

Đáp án: A

Đặt x = sint

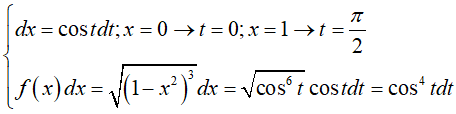
Do đó

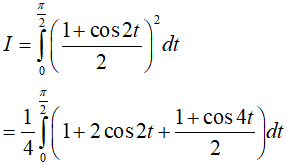
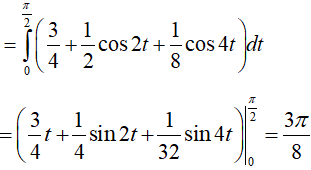
Dạng 3.4. Hàm lượng giác

Ví dụ minh họa

Ví dụ 1. Tính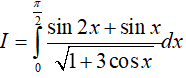

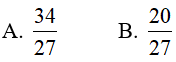
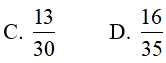
Hướng dẫn:

Đáp án: B

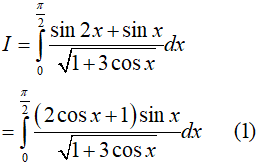
Đặt: t = √(1 + 3 cosx)

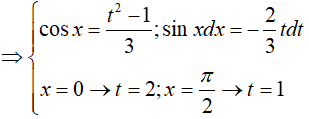
Khi đó

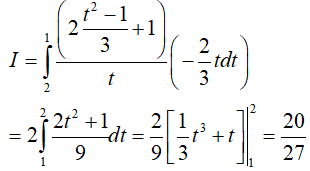
Ví dụ 2. Tính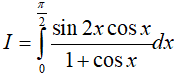

A. 2ln2 − 1    B.ln2 − 1    C. ln2 − 2    D.ln2+ 1

Hướng dẫn:

Đáp án: A

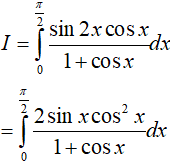
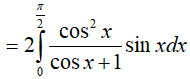
Đặt: t = 1 + cosx

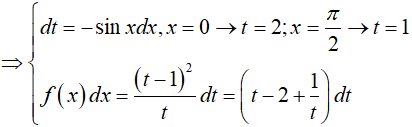
Khi đó

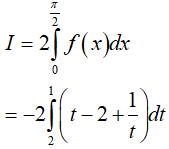
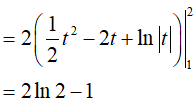
Dạng 3.5. Hàm mũ, logarit

Ví dụ minh họa

Ví dụ 1. Cho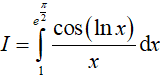

A. I = cos1    B. I = 1    C. I = sin1    D. Đáp án khác

Hướng dẫn:

Đáp án: B

Đặt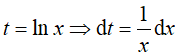

Đổi cận: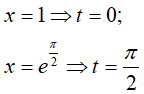

Khi đó:

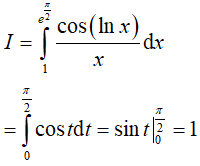
Ví dụ 2. Tính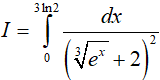

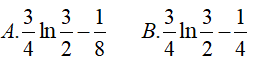
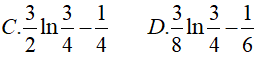
Hướng dẫn:

Đáp án: A

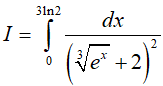
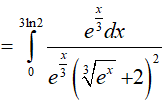
Đặt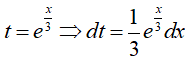

Đổi cận: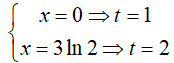

Khi đó:

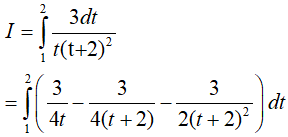
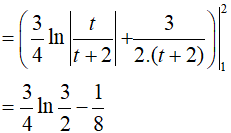
Dạng 3.6. Tích phân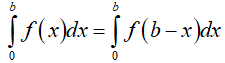

1. Phương pháp giải

Chứng minh:

• Đặt: b − x= t, suy ra x = b − t và dx = −dt,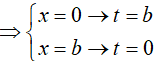

• Do đó: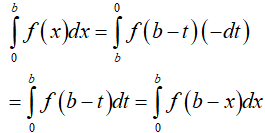

Vì tích phân không phụ thuộc vào biến số

2. Ví dụ minh họa

Ví dụ 1. Tính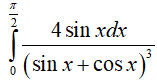

A. 0     B.1     C. 2    D. 3

Hướng dẫn:

Đáp án: C

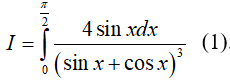
Đặt:

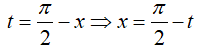
=> dt = −dx; x = 0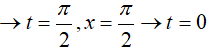

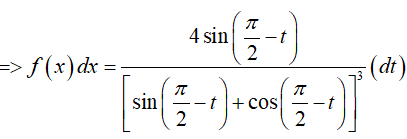
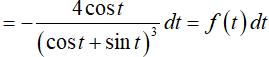
Nhưng tích phân không phụ thuộc và biến số, cho nên:

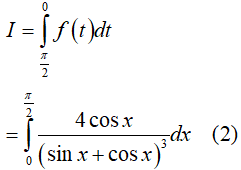
Lấy (1) + (2) vế với vế ta có:

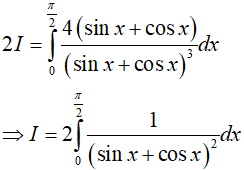
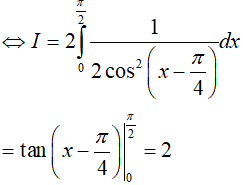
Ví dụ 2. Tính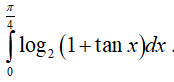

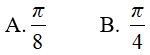
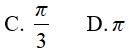
Hướng dẫn:

Đáp án: A

Đặt

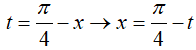
=> dx = −dt; x = 0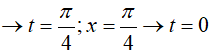

=> f(x)dx = log₂(1 + tanx)dx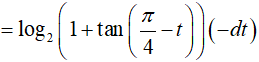

Hay:

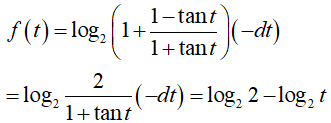
Vậy:

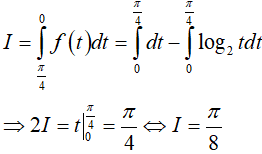
Dạng 3.7. Dạng khác

Ví dụ minh họa

Ví dụ 1. Tính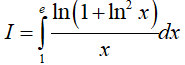

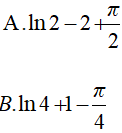
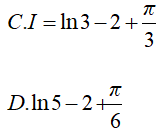
Hướng dẫn:

Đáp án: A

Đặt lnx = t, ta có .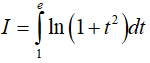

Đặt : u = ln( 1+ t²) ; dv = dt

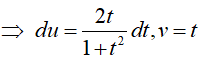
Từ đó có:

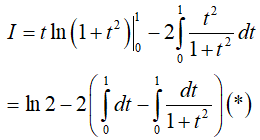
Tiếp tục đặt t = tanu, ta tính được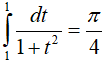

Thay vào (*) ta có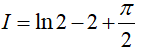

Ví dụ 2. Tính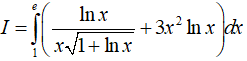

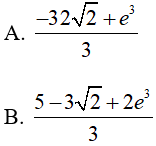
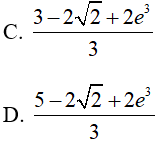
Hướng dẫn:

Đáp án: D

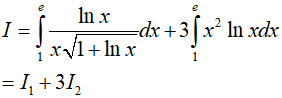
+ Tính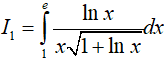

Đặt t = √(1 + lnx) => t² = 1 + lnx;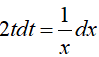

Khi x = 1 => t = 1; x = e => x = √2

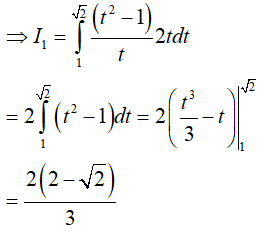
+ Tính .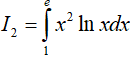

Đặt

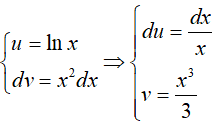
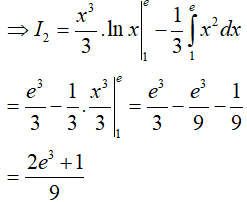
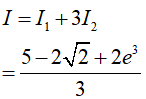
Phương pháp tính tích phân từng phần

Dạng 4.1. Tích phân có dạng: 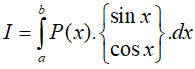trong đó P(x) là đa thức

1. Phương pháp giải

Đặt

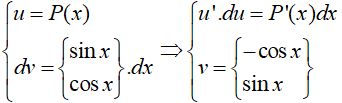
Vậy

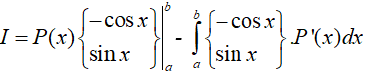
2. Ví dụ minh họa

Ví dụ 1. Tính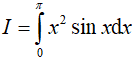

A. π² − 4    B. π² + 4    C. 2π² − 3    D. 2π² + 3

Hướng dẫn:

Đáp án: A

*Đặt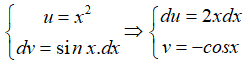

Khi đó:

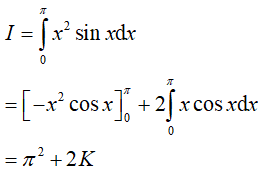
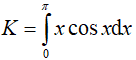
Đặt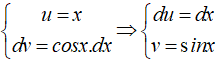

Khi đó:

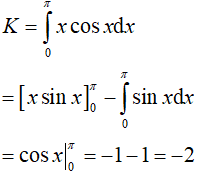
Vậy: I = π² + 2(−2) = π² − 4

Ví dụ 2. Tính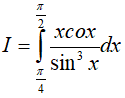

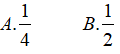
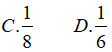
Đáp án: B

Ta có

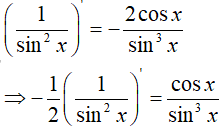
Đặt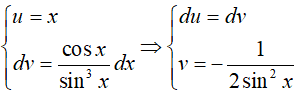

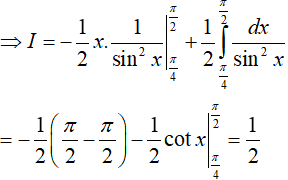
Dạng 4.2. Tích phân có dạng 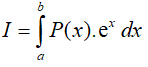trong đó P(x) là đa thức

1. Phương pháp giải

Đặt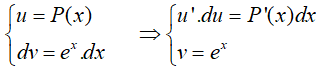

Vậy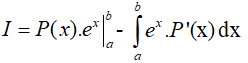

2. Ví dụ minh họa

Ví dụ 1. Tích phân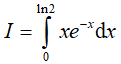

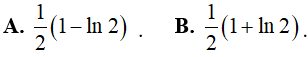
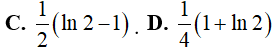
Hướng dẫn:

Đáp án: A

Đặt u = x; dv = e^−x.dx, suy ra du = dx; v = −e^−x

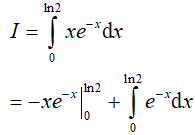
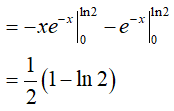
Ví dụ 2. Tìm a > 0 sao cho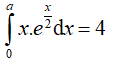

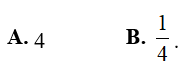
Hướng dẫn:

Đáp án: D

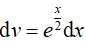
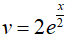
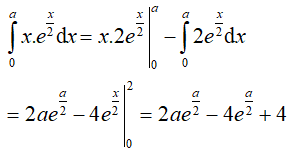
Đặt u = x, , suy ra du = dx,

Theo giả thiết ta có:

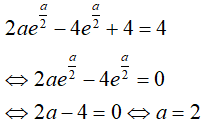
Dạng 4.3. Tích phân có dạng: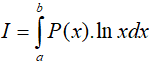

1. Phương pháp giải

Đặt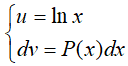

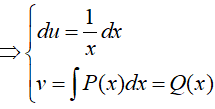
Vậy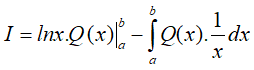

2. Ví dụ minh họa

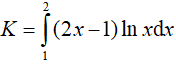
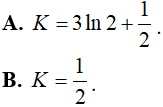
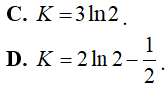
Ví dụ 1. Tích phân bằng:

Hướng dẫn:

Đáp án: D

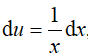
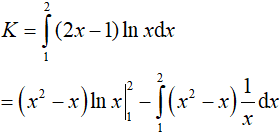
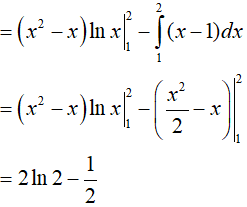
Đặt u = lnx, dv = (2x − 1)dx suy ra , v = x² − x

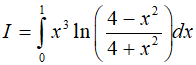
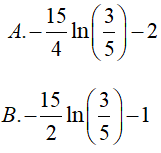
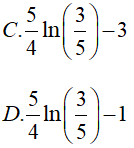
Ví dụ 2. Tính

Hướng dẫn:

Đáp án: A

Đặt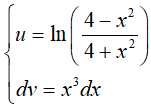

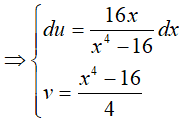
Do đó

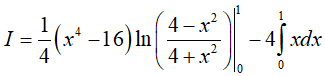
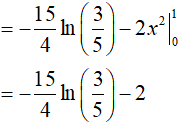
Dạng 4.4. Tích phân có dạng: .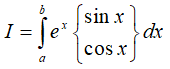

1. Phương pháp giải

Đặt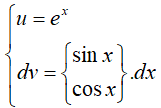

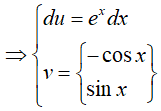
Vậy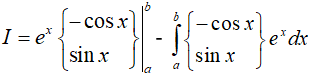

Bằng phương pháp tương tự ta tính được 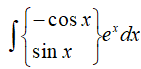sau đó thay vào I.

2. Ví dụ minh họa

Ví dụ 1. Tính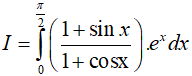

Hướng dẫn:

Đáp án: A

Ta có:

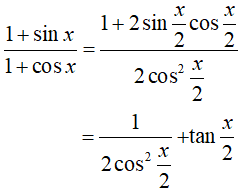
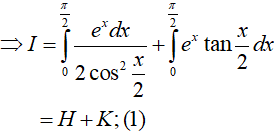
Trong đó

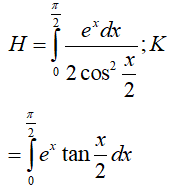
* Ta tính H

Đặt: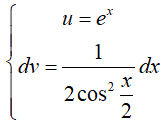

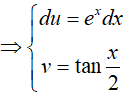
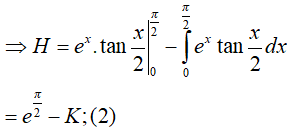
Từ (1) và (2) suy ra,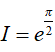

Ví dụ 2. Tính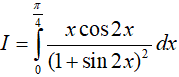

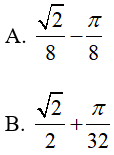
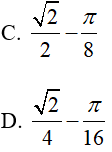
Hướng dẫn:

Đáp án: D

Đặt