Bài tập ôn tập chương II Hình học (mới nhất)

Câu 1:

Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao a$\sqrt{3}$.

A. $2{\mathrm{\pi a}}^2\left(\sqrt{3}-1\right)$

B. ${\mathrm{\pi a}}^2\sqrt{3}$

C. ${\mathrm{\pi a}}^2\left(\sqrt{3}+1\right)$

D. $2{\mathrm{\pi a}}^2\left(\sqrt{3}+1\right)$

Xem lời giải »

Câu 2:

Hình trụ (H) có diện tích xung quanh là 6π(c${\mathrm{m}}^2$) và thể tích khối trụ là 9π(c${\mathrm{m}}^3$). Chiều cao của hình lăng trụ là:

A. 1 (cm)

B. 3 (cm)

C. 1/2 (cm)

D. 2 (cm)

Xem lời giải »

Câu 3:

Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là:

A. $\sqrt{119}$ (cm)

B. 17 (cm)

C. 15 (cm)

D. 13 (cm)

Xem lời giải »

Câu 4:

Một hình nón có đường kính đáy là 2a$\sqrt{3}$, góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a.

A. $3{\mathrm{\pi a}}^3$

B. ${\mathrm{\pi a}}^3$

C. $2\sqrt{3}{\mathrm{\pi a}}^3$

D. $\sqrt{3}{\mathrm{\pi a}}^3$

Xem lời giải »

Câu 5:

Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a$\sqrt{2}$ và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh ${\mathrm{S}}_{\mathrm{xq}}$ của hình nón và thể tích V của khối nón tương ứng là:

A. ${\mathrm{S}}_{\mathrm{xq}}={\mathrm{\pi a}}^2; \mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{12}$

B. ${\mathrm{S}}_{\mathrm{xq}}=\frac{{\mathrm{\pi a}}^2}{2}; \mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{3}}{12}$

C. ${\mathrm{S}}_{\mathrm{xq}}={\mathrm{\pi a}}^2\sqrt{2}; \mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{4}$

D. ${\mathrm{S}}_{\mathrm{xq}}={\mathrm{\pi a}}^2; \mathrm{V}=\frac{{\mathrm{\pi a}}^3\sqrt{6}}{4}$

Xem lời giải »

Câu 6:

Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình chữ nhật có diện tích là 2${\mathrm{a}}^2$. Diện tích xung quanh của hình trụ là:

A. 4π${\mathrm{a}}^2$

B. 3π${\mathrm{a}}^2$

C. 2π${\mathrm{a}}^2$

D. π${\mathrm{a}}^2$

Xem lời giải »

Câu 7:

Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

A. 48π (c${\mathrm{m}}^3$)

B. 24π (c${\mathrm{m}}^3$)

C. 72π (c${\mathrm{m}}^3$)

D. 18π (c${\mathrm{m}}^3$)

Xem lời giải »

Câu 8:

Cho khối trụ có diện tích toàn phần là 6π${\mathrm{a}}^2$và thể tích là 2π${\mathrm{a}}^3$. Bán kính đáy của hình trụ là:

A. 3a/2

B. a

C. 2a/3

D. 2a

Xem lời giải »

Câu 9:

Tam giác ABC vuông đỉnh A có $\widehat{ABC}$ = 60^o và AB = a. Quay miền trong và các cạnh của tam giác ABC quanh trục AB thì ta được khối nón (N). Thể tích của khối nón (N) là:

A. $\frac{{\mathrm{\pi a}}^3\sqrt{3}}{3}$

B. ${\mathrm{\pi a}}^3$

C. $3{\mathrm{\pi a}}^3$

D. $\frac{{\mathrm{\pi a}}^3}{3}$

Xem lời giải »

Câu 10:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Thể tích khối nón có đỉnh là tâm O của hình vuông A'B'C'D' và đáy là hình tròn ngoại tiếp hình vuông ABCD là:

A. $\frac{{\mathrm{\pi a}}^3}{3}$

B. ${\mathrm{\pi a}}^3$

C. $\frac{2{\mathrm{\pi a}}^3}{3}$

D. $\frac{2{\mathrm{\pi a}}^3\sqrt{2}}{3}$

Xem lời giải »

Câu 11:

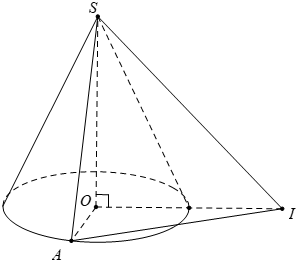
Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R. Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R$\sqrt{3}$. Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI. Biết rằng tam giác SAI vuông cân tại S. Khi đó, diện tích xung quanh ${\mathrm{S}}_{\mathrm{xq}}$ của hình nón và thể tích V của khối nón là:

A. ${\mathrm{S}}_{\mathrm{xq}}={\mathrm{\pi R}}^2\sqrt{2}; \mathrm{V}=\frac{{\mathrm{\pi R}}^3}{3}$

B. ${\mathrm{S}}_{\mathrm{xq}}=2{\mathrm{\pi R}}^2; \mathrm{V}=\frac{2{\mathrm{\pi R}}^3}{3}$

C. ${\mathrm{S}}_{\mathrm{xq}}=\frac{{\mathrm{\pi R}}^2\sqrt{2}}{2}; \mathrm{V}=\frac{{\mathrm{\pi R}}^3}{6}$

D. ${\mathrm{S}}_{\mathrm{xq}}={\mathrm{\pi R}}^2; \mathrm{V}=\frac{2{\mathrm{\pi R}}^3}{3}$

Xem lời giải »

Câu 12:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy và SA = 2a. Góc giữa cạnh bên SB và đáy là 45^o. Bán kính mặt cầu tâm S và tiếp xúc với BD theo a là:

A. $\frac{\mathrm{a}\sqrt{6}}{3}$

B. $\frac{\mathrm{a}\sqrt{6}}{6}$

C. $\frac{\mathrm{a}\sqrt{6}}{2}$

D. $\mathrm{a}\sqrt{6}$

Xem lời giải »

Câu 13:

Cho hình chóp tứ giác đều S.ABCD có AB = a và góc giữa SA và đáy là 60^o. Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) là:

A. $\frac{\mathrm{a}\sqrt{42}}{6}$

B. $\frac{\mathrm{a}\sqrt{42}}{14}$

C. $\frac{\mathrm{a}\sqrt{42}}{7}$

D. $\frac{2\mathrm{a}\sqrt{42}}{7}$

Xem lời giải »

Câu 14:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tạo với mặt phẳng (ABC) một góc là 60^o. Bán kính mặt cầu ngoại tiếp hình chóp là:

A. a$\sqrt{3}$

B. a$\sqrt{2}$

C. a$\sqrt{3}$/2

D. a

Xem lời giải »

Câu 15:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = a; AB' = 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là:

A. 5π${\mathrm{a}}^2$

B. 3π${\mathrm{a}}^2$

C. 5π${\mathrm{a}}^2$/4

D. 5π${\mathrm{a}}^2$/3

Xem lời giải »

Câu 16:

Cho hình lăng trụ đứng tam giác đều ABC.A'B'C' có AA' = 2AB = 2a. Bán kính của mặt cầu ngoại tiếp hình lăng trụ là:

A. $\frac{\mathrm{a}\sqrt{3}}{3}$

B. $\frac{2\mathrm{a}\sqrt{3}}{3}$

C. $\frac{\mathrm{a}\sqrt{39}}{3}$

D. $\frac{\mathrm{a}\sqrt{7}}{2}$

Xem lời giải »

Câu 17:

Cho hình lăng trụ đứng ABC.${\mathrm{A}}_1{\mathrm{B}}_1{\mathrm{C}}_1$ có tất cả các cạnh đều bằng nhau và bằng a. Các đáy của lăng trụ nội tiếp các đường tròn đáy của khối trụ (H). Thể tích của khối trụ là:

A. $\frac{{\mathrm{\pi a}}^3\sqrt{3}}{3}$

B. $\frac{{\mathrm{\pi a}}^3}{3}$

C. $\frac{{\mathrm{\pi a}}^3}{9}$

D. $\frac{3{\mathrm{\pi a}}^3}{4}$

Xem lời giải »

Câu 18:

Cho hình tứ diện ABCD có hai tam giác ΔBCD, ΔACD là hai tam giác đều cạnh a và nằm trên hai mặt phẳng vuông góc với nhau. Bán kính mặt cầu ngoại tiếp hình tứ diện là:

A. $\frac{\mathrm{a}\sqrt{7}}{2}$

B. $\frac{\mathrm{a}}{\sqrt{6}}$

C. $\frac{\mathrm{a}\sqrt{5}}{6}$

D. $\frac{\mathrm{a}\sqrt{15}}{6}$

Xem lời giải »

Câu 19:

Cho hình chóp tam giác đều S.ABC, mặt phẳng (SBC) tạo với đáy một góc bằng 30^o và SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.ABC là:

A. $\frac{52{\mathrm{\pi a}}^3\sqrt{13}}{3}$

B. $\frac{4{\mathrm{\pi a}}^3}{3}$

C. $72{\mathrm{\pi a}}^3\sqrt{2}$

D. Đáp án khác

Xem lời giải »

Câu 20:

Một cái tháp khổng lồ có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn sơn toàn bộ mặt ngoài của tháp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến mét vuông).

A. S = 8243 (${\mathrm{m}}^2$)

B. S = 11762 (${\mathrm{m}}^2$)

C. S = 12667 (${\mathrm{m}}^2$)

D. S = 23524 (${\mathrm{m}}^2$)

Xem lời giải »

Câu 1:

Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P), gọi H là hình chiếu của O trên (P). Nếu R > OH thì:

A. (P) cắt (S)

B. (P) tiếp xúc (S)

C. (P) và (S) không có điểm chung

D. (P) cắt (S) tại hai điểm phân biệt

Xem lời giải »

Câu 2:

Cho mặt cầu (S) có tâm O bán kính R và đường thẳng d. Nếu d và (S) không có điểm chung thì:

A. d(O;d)>R

B. d(O;d)<R

C. d(O;d)=R

D. $d(O;d)\le R$

Xem lời giải »

Câu 3:

Trục đa giác đáy là đường thẳng vuông góc với mặt phẳng đáy tại:

A. Đỉnh đa giác đáy

B. Trực tâm đa giác đáy

C. Trọng tâm đa giác đáy

D. Tâm đường tròn đáy

Xem lời giải »

Câu 4:

Trong không gian, tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:

A. Đường trung trực của đoạn thẳng

B. Trung điểm của đoạn thẳng

C. Mặt phẳng trung trực của đoạn thẳng

D. Đường tròn đường kính là đoạn thẳng đó.

Xem lời giải »

Câu 5:

Công thức tính diện tích mặt cầu là:

A. $S={\mathrm{\pi R}}^2$

B. $S=4{\mathrm{\pi R}}^2$

C. $S=2{\mathrm{\pi R}}^2$

D. $S=\frac{3}{4}{\mathrm{\pi R}}^2$

Xem lời giải »

Câu 6:

Cho các hình sau đây: điểm, đường thẳng, đường tròn. Số hình khi quay quanh một trục cố định ta được mặt tròn xoay là:

A. 1

B. 2

C. 3

D. 0

Xem lời giải »

Câu 7:

Quay đường cong nào sau đây quanh trục đối xứng của nó ta sẽ được một mặt cầu?

A. Elip

B. Parabol

C. Đường tròn

D. Nửa đường tròn

Xem lời giải »

Câu 8:

Cho hai đường thẳng d và d’ cắt nhau tại điểm O và góc giữa hai đường thẳng là $\alpha \left(0^{°}<\alpha <90°\right)$. Quay đường thẳng d’ quanh d thì ta được mặt nón có góc ở đỉnh bằng

A. $2\alpha$

B. $\alpha$

C. $\frac{\alpha }{2}$

D. $4\alpha$

Xem lời giải »

Câu 9:

Quay hình tam giác vuông ABC tại A có  quanh trục là đường thẳng AC ta được hình nón có góc ở đỉnh bằng:

A. $30°$

B. $60°$

C. $90°$

D. $120°$

Xem lời giải »

Câu 10:

Cho tam giác ABC vuông tại A, AH là đường cao. Khi quay các cạnh của tam giác ABC quanh cạnh BC thì số hình nón được tạo thành là mấy hình?

A. 1

B. 0

C. 3

D. 2

Xem lời giải »

Câu 11:

Diện tích xung quanh của hình nón có bán kính đường tròn đáy R và chiều cao h bằng:

A. $S_{xq}=\frac{1}{3}{\mathrm{\pi R}}^2\mathrm{h}$

B. $S_{xq}=\mathrm{\pi R}\sqrt{{\mathrm{R}}^2+{\mathrm{h}}^2}$

C. $S_{xq}=\mathrm{\pi R}\sqrt{{\mathrm{R}}^2-{\mathrm{h}}^2}$

D. $S_{xq}=\mathrm{\pi Rh}$

Xem lời giải »

Câu 12:

Điểm M thuộc khối cầu tâm O bán kính R nếu:

A. OM>R

B. OM=R

C. OM<R

D. $OM\le R$

Xem lời giải »

Câu 13:

Tập hợp các điểm cách đều hai đầu mút của đoạn thẳng là:

A. Đường trung trực của đoạn thẳng

B. Trung điểm của đoạn thẳng

C. Mặt phẳng trung trực của đoạn thẳng

D. Đường tròn đường kính là đoạn thẳng đó

Xem lời giải »

Câu 14:

Cho (P) là mặt phẳng trung trực của đoạn thẳng AB, $M\in \left(P\right)$. Chọn kết luận đúng

A. $M\in AB$

B. M là trung điểm của AB

C. MA=MB

D. MA+MB=AB

Xem lời giải »

Câu 15:

Số mặt phẳng tiếp diện của mặt cầu tại một điểm thuộc mặt cầu là:

A. 0

B. 1

C. 2

D. Vô số

Xem lời giải »

Câu 1:

Chọn mệnh đề sai:

A. Điểm không thuộc khối cầu thì không thuộc mặt cầu

B. Điểm nằm ngoài mặt cầu thì không thuộc khối cầu

C. Điểm không thuộc mặt cầu thì không thuộc khối cầu

D. Điểm nằm trong mặt cầu thì thuộc khối cầu

Xem lời giải »

Câu 2:

Chọn mệnh đề đúng

A. Mặt phẳng cắt mặt cầu là mặt phẳng kính

B. Mặt phẳng chứa đường kính của mặt cầu là mặt phẳng kính

C. Mặt phẳng tiếp xúc với mặt cầu là mặt phẳng kính

D. Mặt phẳng không đi qua điểm nào thuộc mặt cầu là mặt phẳng kính

Xem lời giải »

Câu 3:

Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:

A. $R=\sqrt{r^2+\frac{h^2}{4}}$

B. $R=\sqrt{r^2+\frac{h^2}{2}}$

C. $R=\sqrt{r^2-\frac{h^2}{4}}$

D. $R=r^2+\frac{h^2}{4}$

Xem lời giải »

Câu 4:

Hình lập phương có độ dài cạnh a = 6 thì đường kính mặt cầu ngoại tiếp là:

A. 6

B. $6\sqrt{2}$

C. $6\sqrt{3}$

D. $6\sqrt{6}$

Xem lời giải »

Câu 5:

Cho một lập phương có cạnh bằng a. Tính diện tích mặt cầu nội tiếp hình lập phương đó

A. $S=4{\mathrm{\pi a}}^2$

B. $S={\mathrm{\pi a}}^2$

C. $S=\frac{1}{3}{\mathrm{\pi a}}^2$

D. $S=\frac{4}{3}{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 6:

Cho hình nón có các kích thước r=1cm, l=2cm với r, l lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:

A. $2\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

B. $4\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

C. $3\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

D. $6\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

Xem lời giải »

Câu 7:

Cho hình nón S có bán kính $R=a\sqrt{2}$, góc ở đỉnh bằng $60°$. Diện tích toàn phần của hình nón bằng:

A. $8{\mathrm{\pi a}}^2$

B. $6{\mathrm{\pi a}}^2$

C. $2{\mathrm{\pi a}}^2$

D. $4{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 8:

Cho hình nón có độ dài đường sinh bằng 5, bán kính bằng 3. Diện tích toàn phần của hình nón bằng:

A. $15\mathrm{\pi }$

B. $48\mathrm{\pi }$

C. $39\mathrm{\pi }$

D. $24\mathrm{\pi }$

Xem lời giải »

Câu 9:

Nếu cắt mặt trụ bởi mặt phẳng vuông góc với trục ta được là:

A. Đường elip

B. Đường tròn

C. Hình chữ nhật

D. Hình vuông

Xem lời giải »

Câu 10:

Cho hình vẽ sau, chọn mệnh đề sai:

A. Mặt cầu ngoại tiếp hình nón

B. Hình nón nội tiếp hình trụ

C. Hình trụ nội tiếp mặt cầu

D. Hình nón nội tiếp mặt cầu

Xem lời giải »

Câu 11:

Cho hình (H) dưới đây:

Quay hình (H) quanh trục đối xứng của nó ta được:

A. Hình trụ nội tiếp hình nón

B. Hình nón nội tiếp hình trụ

C. Hình cầu ngoại tiếp hình trụ

D. Hình cầu ngoại tiếp hình nón

Xem lời giải »

Câu 12:

Cho khối nón tròn xoay có đường cao h = 15 cm và đường sinh l = 25cm. thể tích v của khối nón là:

A. $V=2000\mathrm{\pi }\left({\mathrm{cm}}^3\right)$

B. $V=240\mathrm{\pi }\left({\mathrm{cm}}^3\right)$

C. $V=500\mathrm{\pi }\left({\mathrm{cm}}^3\right)$

D. $V=1500\mathrm{\pi }\left({\mathrm{cm}}^3\right)$

Xem lời giải »

Câu 13:

Cho một hình nón có bán kính đáy bằng a và góc ở đỉnh bằng $60°$. Tính diện tích xung quanh của hình nón đó

A. $S_{xq}=4{\mathrm{\pi a}}^2$

B. $S_{xq}=\frac{2\sqrt{3}{\mathrm{\pi a}}^2}{3}$

C. $S_{xq}=\frac{4\sqrt{3}{\mathrm{\pi a}}^2}{3}$

D. $S_{xq}=2{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 14:

Cho hình trụ có bán kính đáy 5cm, chiều cao 4cm. Diện tích toàn phần của hình trụ này là:

A. $96\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

B. $92\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

C. $40\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

D. $90\mathrm{\pi }\left({\mathrm{cm}}^2\right)$

Xem lời giải »

Câu 15:

Cho mặt cầu có diện tích là $72\mathrm{\pi }\left({\mathrm{cm}}^2\right)$. Bán kính R của khối cầu là:

A. $R=\sqrt{6}\left(cm\right)$

B. $R=6\left(cm\right)$

C. $R=3\left(cm\right)$

D. $R=3\sqrt{2}\left(cm\right)$

Xem lời giải »

Câu 1:

Cho điểm M, đường tròn $\left(C_M\right)$ trục $∆$ và các điểm $N\in \left(C_M\right),A\in ∆$. Chọn mệnh đề sai:

A. MN là đường kính

B. $d\left(M,∆\right)=d\left(N,∆\right)$

C. $MN\perp ∆$

D. AM=AN

Xem lời giải »

Câu 2:

Cho hình nón tròn xoay có đường cao h = 40 cm, bán kính đáy r = 50 cm. một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 24 cm. Tính diện tích của thiết diện

A. $S=800\left(c{m}^2\right)$

B. $S=1200\left(c{m}^2\right)$

C. $S=1600\left(c{m}^2\right)$

D. $S=2000\left(c{m}^2\right)$

Xem lời giải »

Câu 3:

Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF

A. $\frac{10{\mathrm{\pi a}}^3}{9}$

B. $\frac{10{\mathrm{\pi a}}^3}{7}$

C. $\frac{5{\mathrm{\pi a}}^3}{2}$

D. $\frac{{\mathrm{\pi a}}^3}{3}$

Xem lời giải »

Câu 4:

Cho một khối trụ có chiều cao bằng 8 cm, bán kính đường tròn đáy bằng 6 cm. cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 4cm. Diện tích của thiết diện được tạo thành là:

A. $32\sqrt{3}\left(c{m}^2\right)$

B. $16\sqrt{3}\left(c{m}^2\right)$

C. $32\sqrt{5}\left(c{m}^2\right)$

D. $16\sqrt{3}\left(c{m}^2\right)$

Xem lời giải »

Câu 5:

Cho hình lăng trụ đứng có đáy là tam giác với độ dài cạnh đáy lần lượt là 5cm, 13cm, 12cm. Một hình trụ có chiều cao bằng 8cm ngoại tiếp lăng trụ đã cho có thể tích bằng

A. $V=338{\mathrm{\pi cm}}^3$

B. $V=386{\mathrm{\pi cm}}^3$

C. $V=507{\mathrm{\pi cm}}^3$

D. $V=338{\mathrm{cm}}^3$

Xem lời giải »

Câu 6:

Cho hình chóp S.ABC có $SA\perp \left(ABC\right);SA=a$ đáy ABC là tam giác vuông tại B, $\widehat{BAC}=60°$ và $AB=\frac{a}{2}$. Gọi (S) là mặt cầu ngoại tiếp hình chóp S.ABC. Tìm mệnh đề sai.

A. Diện tích của (S ) là $\frac{2{\mathrm{\pi a}}^2}{3}$

B. Tâm của (S) là trung điểm SC

C. (S) có bán kính $\frac{a\sqrt{2}}{2}$

D. Thể tích khối cầu là $\frac{\sqrt{2}{\mathrm{\pi a}}^3}{3}$

Xem lời giải »

Câu 7:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại A, $AB=2a\sqrt{3}$. Đường chéo BC’ tạo với mặt phẳng (AA’C’C) một góc bằng $60°$. Gọi (S) là mặt cầu ngoại tiếp hình lăng trụ đã cho. Bán kính của mặt cầu (S) bằng:

A. $\frac{a}{2}$

B. a

C. 3a

D. 2a

Xem lời giải »

Câu 8:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.

A. $V=\frac{{\mathrm{\pi a}}^2\mathrm{h}}{9}$

B. $V=\frac{{\mathrm{\pi a}}^2\mathrm{h}}{3}$

C. $3{\mathrm{\pi a}}^2\mathrm{h}$

D. $V=\frac{{\mathrm{\pi a}}^2\mathrm{h}}{27}$

Xem lời giải »

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, $\widehat{ABC}=120°$ , tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC

A. $\frac{\sqrt{41}}{6}a$

B. $\frac{\sqrt{37}}{6}a$

C. $\frac{\sqrt{39}}{6}a$

D. $\frac{\sqrt{35}}{6}a$

Xem lời giải »

Câu 10:

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Diện tích xung quanh $S_{xq}$ của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD là:

A. $S_{xq}=\frac{{\mathrm{\pi a}}^2\sqrt{17}}{4}$

B. $S_{xq}={\mathrm{\pi a}}^2$

C. $S_{xq}=\frac{{\mathrm{\pi a}}^2\sqrt{17}}{2}$

D. $S_{xq}={\mathrm{\pi a}}^2\sqrt{17}$

Xem lời giải »

Câu 11:

Người ta thả một viên billiards có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng:

A. 4,2cm

B. 3,6cm

C. 2,6cm

D. 2,7cm

Xem lời giải »

Câu 12:

Một hình nón đỉnh S có bán kính đáy bằng $2a\sqrt{3}$, góc ở đỉnh là $120°$. Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất $S_{max}$ của thiết diện đó là bao nhiêu?

A. $S_{max}=8a^2$

B. $S_{max}=4a^2\sqrt{2}$

C. $S_{max}=4a^2$

D. $S_{max}=16a^2$

Xem lời giải »

Câu 13:

Một khối đồ chơi có dạng khối nón, chiều cao bằng 20cm, trong đó có chứa một lượng nước. Nếu đặt khối đồ chơi theo hình H1 thì chiều cao của lượng nước bằng $\frac{2}{3}$ chiều cao của khối nón. Hỏi nếu đặt khối đồ chơi theo hình H2 thì chiều cao h của lượng nước trong khối đó gần với giá trị nào sau đây?

A. 2,21cm

B. 5,09cm

C. 6,67cm

D. 5,93cm

Xem lời giải »

Câu 14:

Cho tứ diện ABCD có $AD\perp \left(ABC\right)$, ABC là tam giác vuông tại B. Biết $BC=a, AB=a\sqrt{3},AD=3a$. Quay các tam giác ABC và ABD (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng:

A. $\frac{8\sqrt{3}{\mathrm{\pi a}}^3}{3}$

B. $\frac{3\sqrt{3}{\mathrm{\pi a}}^3}{16}$

C. $\frac{5\sqrt{3}{\mathrm{\pi a}}^3}{16}$

D. $\frac{4\sqrt{3}{\mathrm{\pi a}}^3}{16}$

Xem lời giải »

Câu 15:

Có 4 viên bi hình cầu bán kính bằng 1 cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đặt 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc với cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng:

A. $\frac{7}{2}$

B. $\frac{6+2\sqrt{6}}{3}$

C. $\frac{3+2\sqrt{6}}{3}$

D. $\frac{4\sqrt{6}}{3}$

Xem lời giải »

Câu 1:

Cho mặt cầu (S). Nếu (P) là mặt phẳng kính của mặt cầu (S) thì:

A. (P) tiếp xúc (S)

B. (P) không cắt (S)

C. (P) không đi qua tâm mặt cầu

D. (P) đi qua tâm mặt cầu

Xem lời giải »

Câu 2:

Khi quay hình chữ nhật ABCD quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?

A. AB và AD

B. AC và AB

C. BD và AC

D. BC và AD

Xem lời giải »

Câu 3:

Khi quay hình chữ nhật MNPQ quanh đường thẳng AB với A, B lần lượt là trung điểm của MN, PQ ta được một hình trụ có đường kính đáy:

A. MA

B. AB

C. MQ

D. MN

Xem lời giải »

Câu 4:

Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, CD. Quay hình chữ nhật quanh trục MN ta được hình trụ có bán kính đáy là:

A. MN

B. AB

C. CM

D. AM

Xem lời giải »

Câu 5:

Một hình hộp chữ nhật có độ dài 3 cạnh lần lượt là 2, 2, 1. Tính bán kính R mặt cầu ngoại tiếp hình hộp nói trên.

A. R=3

B. R=9

C. $R=\frac{3}{2}$

D. $R=\frac{9}{2}$

Xem lời giải »

Câu 6:

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, AD=2a, AA'=2a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABB’C’

A. $R=3a$

B. $R=\frac{3a}{4}$

C. $R=\frac{3a}{2}$

D. R=2a

Xem lời giải »

Câu 7:

Một hình nón có thiết diện qua trục là tam giác đều cạnh a. Tính bán kính mặt cầu ngoại tiếp hình nón theo a.

A. $\frac{2a}{\sqrt{3}}$

B. $\frac{a}{3\sqrt{3}}$

C. $\frac{2a}{3\sqrt{3}}$

D. $\frac{a}{\sqrt{3}}$

Xem lời giải »

Câu 8:

Cho hình chóp ta giác S.ABC có $\widehat{SAC}=\widehat{SBC}=90°$. Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?

A. SA

B. SB

C. SC

D. AC

Xem lời giải »

Câu 9:

Thể tích của khối cầu bán kính a bằng:

A. $\frac{4{\mathrm{\pi a}}^3}{3}$

B. $4{\mathrm{\pi a}}^3$

C. $\frac{{\mathrm{\pi a}}^3}{3}$

D. $2{\mathrm{\pi a}}^3$

Xem lời giải »

Câu 10:

Cho hình nón có các kích thước r=1; h=2 với r. h lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:

A. $3\mathrm{\pi }$

B. $1+\sqrt{5}\mathrm{\pi }$

C. $\left(\sqrt{3}+1\right)\mathrm{\pi }$

D. $\left(\sqrt{5}+1\right)\mathrm{\pi }$

Xem lời giải »

Câu 11:

Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón bằng

A. $18{\mathrm{\pi a}}^2$

B. $12{\mathrm{\pi a}}^2$

C. $36{\mathrm{\pi a}}^2$

D. $20{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 12:

Số hình nón có được khi quay hình sau quanh trục BC là:

A. 1

B. 2

C. 3

D. 4

Xem lời giải »

Câu 13:

Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc $\alpha \left(0°<\alpha <90°\right)$ thì ta được:

A. Đường tròn

B. Hình chữ nhật

C. Hình thang cân

D. Elip

Xem lời giải »

Câu 14:

Cho khối (N) có bán kính đáy bằng 3 và diện tích xung quanh bằng $15\mathrm{\pi }$. Tính thể tích V của khối nón (N)

A. $V=12\mathrm{\pi }$

B. $V=20\mathrm{\pi }$

C. $V=36\mathrm{\pi }$

D. $V=60\mathrm{\pi }$

Xem lời giải »

Câu 15:

Cho một khối trụ có độ dài đường sinh l và bán kính đường tròn đáy là r. Diện tích toàn phần của hình trụ là:

A. $S_{tp}=\mathrm{\pi r}\left(\mathrm{l}+\mathrm{r}\right)$

B. $S_{tp}=2\mathrm{\pi r}\left(\mathrm{l}+2\mathrm{r}\right)$

C. $S_{tp}=\mathrm{\pi r}\left(2\mathrm{l}+\mathrm{r}\right)$

D. $S_{tp}=2\mathrm{\pi r}\left(\mathrm{l}+\mathrm{r}\right)$

Xem lời giải »

Câu 16:

Cho khối trụ có hai đáy là hình tròn (O;R) và (O';R), OO'=4R. Trên đường tròn tâm O lấy hai điểm A, B sao cho $AB=R\sqrt{3}$. Mặt phẳng (P) đi qua A, B cắt OO’ và tạo với đáy một góc bằng $60°$. (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng:

A. $\left(\frac{4\mathrm{\pi }}{3}-\frac{\sqrt{3}}{2}\right)R^2$

B. $\left(\frac{2\mathrm{\pi }}{3}+\frac{\sqrt{3}}{4}\right)R^2$

C. $\left(\frac{4\mathrm{\pi }}{3}+\frac{\sqrt{3}}{2}\right)R^2$

D. $\left(\frac{2\mathrm{\pi }}{3}-\frac{\sqrt{3}}{4}\right)R^2$

Xem lời giải »

Câu 17:

Một cái phễu có dạng hình nón có chiều cao 15 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng $\frac{1}{5}$ chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn)

A. 0,577cm

B. 0,216cm

C. 0,325cm

D. 0,188cm

Xem lời giải »

Câu 18:

Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?

A. $\left(20\sqrt[3]{7}-10\right)cm$

B. $10\sqrt[3]{7}cm$

C. $\left(20-10\sqrt[3]{7}\right)cm$

D. $20\sqrt[3]{7}cm$

Xem lời giải »

Câu 19:

Cho hình chóp S.ABCD có $\widehat{ABC}=\widehat{ADC}=90°$, cạnh bên SA vuông góc với (ABCD), góc tạo bởi SC và đáy ABCD bằng $60°$, CD = a và tam giác ADC có diện tích bằng $\frac{a^2\sqrt{3}}{2}$. Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD là:

A. $S_{mc}=16{\mathrm{\pi a}}^2$

B. $S_{mc}=4{\mathrm{\pi a}}^2$

C. $S_{mc}=32{\mathrm{\pi a}}^2$

D. $S_{mc}=8{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 20:

Cho hình nón $N_1$ có chiều cao bằng 40 cm. gười ta cắt hình nón $N_1$ bằng một mặt phẳng song song với đáy của nó để được một hình nón nhỏ $N_2$ có thể tích bằng $\frac{1}{8}$ thể tích $N_1$. Tính chiều cao h của hình nón $N_2$?

A. 20cm

B. 10cm

C. 5cm

D. 40cm

Xem lời giải »

Câu 21:

Cho hình chóp S.ABC có đáy là tam giác ABC đều, đường cao SH với H nằm trong tam giác ABC và 2SH=BC, (SBC) tạo với mặt phẳng (ABC) một góc $60°$. Biết có một điểm O nằm trên đường cao SH sao cho $d\left(O;AB\right)=d\left(O;AC\right)=d\left(O;\left(SBC\right)\right)=1$. Tính thể tích khối cầu ngoại tiếp hình chóp đã cho.

A. $\frac{500\mathrm{\pi }}{81}$

B. $\frac{343\mathrm{\pi }}{48}$

C. $\frac{256\mathrm{\pi }}{81}$

D. $\frac{125\mathrm{\pi }}{162}$

Xem lời giải »

Câu 22:

Cho hình trụ có chiều cao $h=a\sqrt{3}$, bán kính đáy r=a. Gọi O, O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai đường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng $30°$. Khoảng cách giữa hai đường thẳng AB và OO’ bằng:

A. $a\sqrt{6}$

B. $\frac{a\sqrt{6}}{2}$

C. $a\sqrt{3}$

D. $\frac{a\sqrt{3}}{2}$

Xem lời giải »

Câu 23:

Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4. Tổng độ dài đường kính của hai quả bóng đó.

A. 6

B. 14

C. 12

D. 10

Xem lời giải »

Câu 24:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, $AB=a\sqrt{3}, BC=2a$, đường thẳng AC’ tạo với mặt phẳng (BCC’B’) một góc $30°$. Diện tích mặt cầu ngoại tiếp lăng trụ đã cho bằng:

A. $24{\mathrm{\pi a}}^2$

B. $6{\mathrm{\pi a}}^2$

C. $4{\mathrm{\pi a}}^2$

D. $3{\mathrm{\pi a}}^2$

Xem lời giải »

Câu 25:

Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S và có đường tròn đáy là đường tròn tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là:

A. $\frac{1}{4}$

B. $\frac{1}{2}$

C. $\frac{2}{3}$

D. $\frac{1}{3}$

Xem lời giải »

Câu 26:

Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có cùng chiều cao. Tỉ lệ thể tích khối gỗ cần phải đẽo đi ít nhất (tính gần đúng) là:

A. 30%

B. 50%

C. 21%

D. 11%

Xem lời giải »

Câu 27:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, $AB=AC=a$ và $AA\text{'}=a\sqrt{2}$. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:

A. $\frac{{\mathrm{\pi a}}^3}{3}$

B. ${\mathrm{\pi a}}^3$

C. $\frac{4{\mathrm{\pi a}}^3}{3}$

D. $4{\mathrm{\pi a}}^3$

Xem lời giải »

Câu 28:

Một hộp đựng phấn hình hộp chữ nhật có chiều dài 30 cm, chiều rộng 5 cm và chiều cao 6 cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao h = 6 cm và bán kính đáy $r=\frac{1}{2}$cm. Hỏi có thể xếp được tối đa bao nhiêu viên phấn.

A. 150

B. 151

C. 153

D. 154

Xem lời giải »

Câu 29:

Cho hình trụ có chiều cao bằng $6\sqrt{2}$ cm. Biết rằng một mặt phẳng không vuông góc với đáy và cắt hai mặt đáy theo hai dây cung song song AB, CD mà AB=CD=6cm, diện tích tứ giác ABCD bằng $60c{m}^2$. Tính bán kính đáy của hình trụ.

A. 5cm

B. $3\sqrt{2}cm$

C. $5\sqrt{2}cm$

D. 4cm

Xem lời giải »

Câu 30:

Cho hình nón tròn xoay đỉnh S, đáy là hình tròn tâm O. Trên đường tròn đó lấy hai điểm A và M. Biết góc $\widehat{AOM}=60°$, góc tạo bởi hai mặt phẳng (SAM) và (OAM) có số đo bằng $30°$ và khoảng cách từ O đến (SAM) bằng 2. Khi đó thể tích khối nón là:

A. $\frac{32\sqrt{3}}{27}\mathrm{\pi }$

B. $\frac{256\sqrt{3}}{9}\mathrm{\pi }$

C. $\frac{256\sqrt{3}}{27}\mathrm{\pi }$

D. $\frac{32\sqrt{3}}{9}\mathrm{\pi }$

Xem lời giải »

Câu 31:

Cho hình trụ (T) có (C),(C') là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhậ kích thước 1 x 2 (như hình vẽ dưới đây). Thể tích của khối trụ (T) là

A. $250\mathrm{\pi }$

B. $100\mathrm{\pi }$

C. $\frac{100\mathrm{\pi }}{3}$

D. $\frac{250\mathrm{\pi }}{3}$

Xem lời giải »

Câu 32:

Cho tam giác nhọn ABC. Khi quay ABC quanh các cạnh BC, CA, AB ta được các hình tròn xoay có thể tích lần lượt là $\frac{3136\mathrm{\pi }}{5};\frac{9048\mathrm{\pi }}{13};672\mathrm{\pi }$. Tính diện tích tam giác ABC?

A. S=84

B. S=336

C. S=91

D. S=1295

Xem lời giải »

Câu 33:

Cho tam giác ABC vuông cân tại A có AB=AC=12. Lấy một điểm M thuộc cạnh huyền BC và gọi H là hình chiếu của M lên cạnh góc vuông AB. Quay tam giác AMH quanh trục là đường thẳng AB tạo thành mặt nón tròn xoay (N), hỏi thể tích V của khối nón tròn xoay (N) lớn nhất là bao nhiêu?

A. $V=\frac{128\mathrm{\pi }}{3}$

B. $V=256\mathrm{\pi }$

C. $V=\frac{256\mathrm{\pi }}{3}$

D. $V=72\mathrm{\pi }$

Xem lời giải »

Câu 34:

Tứ diện ABCD có $AB=2,CD=2\sqrt{2}$ $\widehat{ABC}=\widehat{DAB}=90°$ và góc giữa AD, BC bằng $45°$. Khi đó, bán kính mặt cầu ngoại tiếp tứ diện là:

A. $\sqrt{2}$

B. $\sqrt{3}$

C. $2\sqrt{3}$

D. $\sqrt{5}$

Xem lời giải »

Câu 35:

Cho hình chóp S.ABC có SA vuông góc với đáy và $SA=a\sqrt{2}; \widehat{BAC}=45°$. Biết bán kính mặt cầu ngoại tiếp hình chóp S.ABC bằng a. Tính độ dài cạnh BC.

A. BC=a

B. BC=2a

C. $BC=a\sqrt{2}$

D. $BC=\frac{a}{\sqrt{2}}$

Xem lời giải »