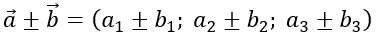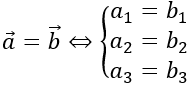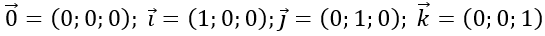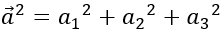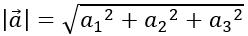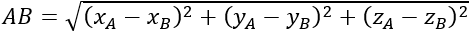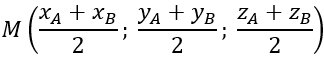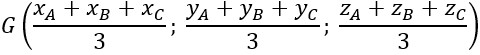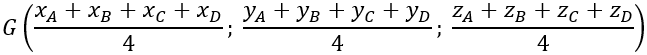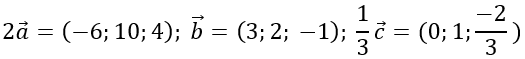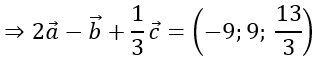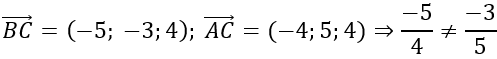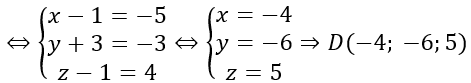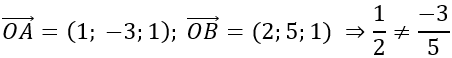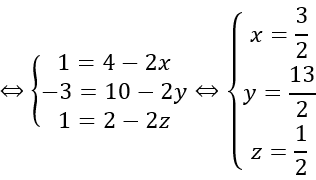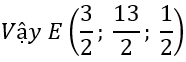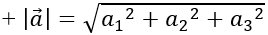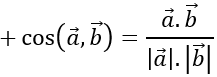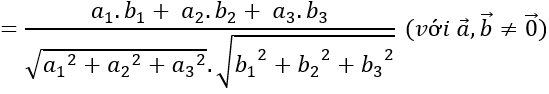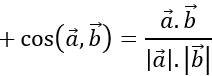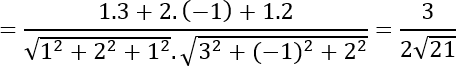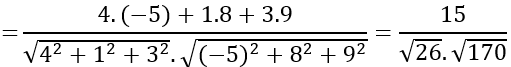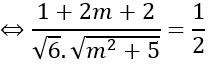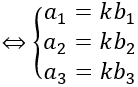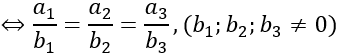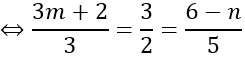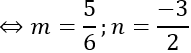Các dạng bài tập Hệ tọa độ trong không gian chọn lọc, có đáp án - Toán lớp 12

---

Các dạng bài tập Hệ tọa độ trong không gian chọn lọc, có đáp án

Với Các dạng bài tập Hệ tọa độ trong không gian chọn lọc, có đáp án Toán lớp 12 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ tọa độ trong không gian từ đó đạt điểm cao trong bài thi môn Toán lớp 12.

• 4 dạng bài tập về Hệ tọa độ trong không gian trong đề thi Đại học có lời giải Xem chi tiết
• Dạng 1: Tìm tọa độ của vecto, của điểm Xem chi tiết
• Dạng 2: Tích vô hướng của hai vecto trong không gian Xem chi tiết
• Dạng 3: Chứng minh hai vecto cùng phương, không cùng phương Xem chi tiết
• Dạng 4: Tích có hướng của hai vecto trong không gian Xem chi tiết

Tìm tọa độ của vecto, của điểm

A. Phương pháp giải & Ví dụ

1. Tọa độ của vecto

a) Định nghĩa

Ta gọi bộ ba số (x; y; z) là tọa độ của vecto u→ đối với hệ tọa độ Oxyz cho trước

     u→=(x;y;z)⇔u→=xi→+yj→+zk→

b) Tính chất

Trong không gian Oxyz, cho hai vecto a→ =(a₁;a₂;a₃ ) và b→ =(b₁;b₂;b₃ ); k∈R

+

+

+

+

+

+

2. Tọa độ của điểm

a) Định nghĩa

M(x;y;z)⇔OM→= xi→+yj→+zk→(x: hoành độ, y: tung độ, z: cao độ)

b) Tính chất

Cho A(x _A; y _A; z _A );B(x _B; y _B; z _B )

+ AB→ =(x_A-x_B;y_A-y_B;z_A-z_B )

+

+ Tọa độ trung điểm M của đoạn thẳng AB:

+

+ Tọa độ trọng tâm G của tam giác ABC:

+

+ Tọa độ trọng tâm G của tứ diện ABCD:

+

Ví dụ minh họa

Bài 1:Trong hệ trục tọa độ Oxyz, cho các vecto a→ =-3i→ +5j→ +2k→ ; b→ =(3;2; -1); c→ =3j→ -2k→ ; d→ =(5; -3;2)

a) Tìm tọa độ của các vecto a→ - 2b→ + c→ ; 3b→ -2c→ +d→

b) Tìm tọa độ của vecto 2a→ -b→ +1/3c→

c) Phân tích vecto d→ theo 3 vecto a→ ; b→ ; c→

Hướng dẫn:

a) a→ =(-3;5;2); 2b→ =(6;4; -2); c→ =(0;3; -2)

⇒ a→- 2 b→+ c→=(-9;4; 2)

3 b→=(9;6; -3); 2 c→=(0;6; -4); d→=(5; -3;2)

⇒3 b→-2 c→+ d→=(14; -3;7)

b)

c) giả sử d→=ma→+nb→+pc→

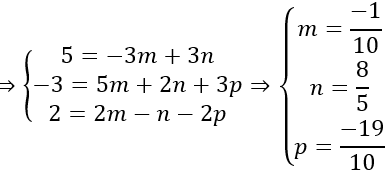
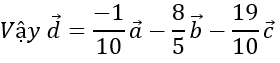
Bài 2:Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1; -3;1);B(2;5;1) và vecto OC→=-3 i→+2 j→+5 k→

a) Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

b) Tìm tọa độ điểm E sao cho tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

c) Tìm tọa độ điểm M sao cho 3 AB→+2 AM→=3 CM→

Hướng dẫn:

a)

⇒BC→; AC→ không cùng phương hay A, B, C không thẳng hàng

Gọi D (x; y; z) ⇒AD→=(x-1;y+3;z-1)

ABCD là hình bình hành ⇔AD→=BC→

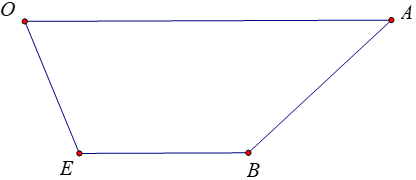
b)

Ta có:

⇒OA→; OB→ không cùng phương hay O, A, B không thẳng hàng.

Gọi E (x; y; z) ⇒EB→=(2-x;5-y;1-z)

Theo đề bài, tứ giác OABE là hình thang có hai đáy OA, BE và OA = 2BE.

⇒OA→=2EB→

c) Gọi M (x; y; z). Ta có:

AB→=(1;8;0)⇒3AB→=(3;24;0)

AM→=(x-1;y+3;z-1)⇒2AM→=(2x-2;2y+6;2z-2)

CM→=(x+3;y-2;z-5)⇒3CM→=(3x+9;3y-6;3z-15)

3AB→+2AM→=3CM→

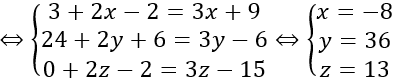
Vậy M(-8; 36; 13)

Công thức tính Tích vô hướng của hai vecto trong không gian

A. Phương pháp giải & Ví dụ

+ Tích vô hướng của hai vecto:

    a→.b→=a₁.b₁+ a₂.b₂+ a₃.b₃

+ a→⊥b→⇔a₁.b₁+ a₂.b₂+ a₃.b₃=0

+ a→²=a₁²+a₂²+a₃²

Ví dụ minh họa

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),

b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.

a) Tính a→.b→; b→(a→-2c→)

b) So sánh a→.(b→.c→) và (a→.b→ ) c→

c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )

d) Tìm m để u→⊥(b→+d→)

e) Tìm m để (u→,a→ )=60⁰

Hướng dẫn:

a) a→ =(1;2;1),b→ =(3;-1;2)

⇒a→ .b→ =1.3+2.(-1)+1.2=3.

c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)

⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11

b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)

a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)

Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→

c) Ta có:

⇒(a→.b→ )≈71⁰

+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)

⇒cos( a→+b→,3a→- 2c→ )

⇒( a→ +b→ ,3a→ - 2c→ )≈77⁰

d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)

u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0

e)

(u→ ,a→ )=60⁰⇔cos⁡(u→ ,a→ )=1/2

Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=120⁰,

|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |

Hướng dẫn:

Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos⁡(a→ ,b→ )

Ta có: |a→ + b→ |²=(a→ + b→ )²=a→ ²+2a→ .b→ +b→ ²

=|a→ |²+|b→ |²+2|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7

⇒|a→ + b→ |=√7

Tương tự:

|a→ -2b→ |² =|a→ |²+4|b→ |²-4|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52

⇒|a→ -2b→ |=2√(13)

Chứng minh hai vecto cùng phương, không cùng phương

A. Phương pháp giải & Ví dụ

a→cùng phương với b→ (b→ ≠ 0→ )⇔ a→=k b→ (k∈R)

Ví dụ minh họa

Bài 1: Trong không gian hệ tọa độ Oxyz, cho các vecto a→=(3;2;5),

b→ =(3m+2;3;6-n). Tìm m, n để a→ , b→ cùng phương,

Hướng dẫn:

Ta có: a→=(3;2;5), b→=(3m+2;3;6-n).

a→ , b→ cùng phương

Bài 2: Trong không gian hệ trục Oxyz, cho các điểm A (1; 2; 3), B(2; 1; 1), C (0; 2; 4)

a) Chứng minh A, B, C là 3 đỉnh của một tam giác.

b) Tìm tọa độ điểm M thuộc mặt phẳng Oyz sao cho 3 điểm A, B, M thẳng hàng.

Hướng dẫn:

a) Ta có: AB→=(1; -1; -2), AC→=(-1;0;1)

⇒ AB→, AC→ không cùng phương

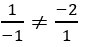
b) M∈(Oyz)⇒M(0;y;z)

AM→ =(-1;y-2;z-3), AB→=(1; -1; -2)

A, B, M thẳng hàng ⇔ AM→, AB→ cùng phương

⇔y=3;z=5

Vậy M (0; 3; 5)

Bài 3: Trong không gian với hệ toạ độ Oxyz, cho tứ giác ABCD có A(2; -1; 5), B(5; -5; 7), C(11; -1; 6), D(5; 7; 2) . Tứ giác ABCD là hình gì?

Hướng dẫn:

AB→=(3; -4;2)

DC→=(6; -8;4)

⇒ DC→=2 AB→ hay DC // AB

⇒ Tứ giác ABCD là hình thang có đáy AB và CD