Bài tập ôn tập chương III Hình học (mới nhất)

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm 50 bài tập Bài tập ôn tập chương III Hình học Toán 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.

Bài tập ôn tập chương III Hình học

Câu 1:

Cho hai điểm A(1;3;5), B(1;-1;1), khi đó trung điểm I của AB có tọa độ là:

A.I(0;-4;-4)

B.I(2;2;6)

C.I(0;-2;-4)

D.I(1;1;3)

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a} = (1; 2; 3), \vec{b} = (- 2; 3; - 1)$ . Khi đó $\vec{a} + \vec{b}$ có tọa độ là:

A.(-1;5;2)

B.(3;-1;4)

C.(1;5;2)

D.(1;-5;-2)

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(5;2;0). Khi đó:

A. $|\vec{A B}|$ = 5

B. $|\vec{A B}|$ = 2 $\sqrt{3}$

C. $|\vec{A B}|$ = $\sqrt{61}$

D. $|\vec{A B}|$ = 3

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz, cho hai véctơ $\vec{a}$ =(2;-3;1) và =(-1;0;4). Tìm tọa độ véctơ $\vec{u}$ =-2 $\vec{a}$ +3.

A.=(-7;6;-10)

B.=(-7;6;10)

C.=(7;6;10)

D.=(-7;-6;10)

Xem lời giải »

Câu 5:

Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D'. Biết A(2;4;0), B(4;0;0), C(-1;4;-7) và D'(6;8;10). Tọa độ điểm B' là:

A. B'(8;4;10)

B. B'(6;12;0)

C. B'(10;8;6)

D. B'(13;0;17).

Xem lời giải »

Câu 6:

#2H3Y1-1~Trong không gian với hệ tọa độ Oxyz, cho véc-tơ =(1;2;0). Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 7:

#2H3Y1-1~Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(2; 1; -1), B(3; 3; 1), C(4; 5; 3). Khẳng định nào đúng?

B. A, B, C thẳng hàng

C. AB = AC

D. O, A, B, C là 4 đỉnh của một tứ diện.

Xem lời giải »

Câu 8:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; -4; - 5). Tìm tọa độ điểm A' đối xứng với A qua mặt phẳng (Oxz) là:

A. (1;- 4;5)

B. (- 1;4;5)

C. (1;4;5)

D. (1;4;- 5).

Xem lời giải »

Câu 9:

#2H3Y1-1~Trong không gian Oxyz, cho véc-tơ sao cho . Tọa độ của véc-tơ là:

A. (-2;1;2)

B. (1;2;-2)

C. (2;1; -2)

D. (2;1;2).

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho hai vec-tơ .

Tính $\vec{x} = 3 \vec{a} + 2 \vec{b}$ .

Xem lời giải »

Câu 11:

#HK2-Sở Bến Tre - 2018~#2H3Y1-1~Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm M(-2;6;1) và M'(a;b;c) đối xứng nhau qua mặt phẳng (Oyz).

Tính S = 7a - 2b + 2017c - 1.

A. S = 2017

B. S = 2042

C. S = 0

D. S = 2018.

Xem lời giải »

Câu 12:

Trong hệ tọa độ Oxyz, cho . Tìm tọa độ của điểm A.

A. (3;0;-1)

B. (-1;0;3)

C. (-1;3;0)

D. (3;-1;0).

Xem lời giải »

Câu 13:

#2H3Y1-1~Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với điểm A qua gốc tọa độ O là:

A. A'(3;-2;1)

B. A'(3;2;-1)

C. A'(3;-2;-1)

D. A'(3;2;1).

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho véc-tơ =(1;0;-2). Trong các véc-tơ sau đây, véc-tơ nào không cùng phương với véc-tơ ?

Xem lời giải »

Câu 15:

#2H3Y1-1~Trong không gian với hệ toạ độ Oxyz, hình chiếu của điểm M(1;-3;-5) trên mặt phẳng (Oyz) có toạ độ là:

A. (0;-3;0)

B. (0;-3;-5)

C. (0;-3;5)

D. (1;-3;0).

Xem lời giải »

Câu 16:

Trong không gian Oxyz, cho điểm M(3;-1;2). Tìm tọa độ điểm N đối xứng với M qua mặt phẳng (Oyz).

A. N(0;-1;2)

B. N(3;1;-2)

C. N(-3;-1;2)

D. N(0;1;1).

Xem lời giải »

Câu 17:

#Nguyễn Tài Chung, 12EX-7~Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC.

A. G(-1/3; 1; -2/3)

B. G(-1;3;-2)

C. G(1/3; -1; 2/3)

D. G(-1/2; 5/2; -5/2).

Xem lời giải »

Câu 18:

Trong không gian Oxyz, cho các điểm A(-1;2;-3), B(2;-1;0). Tìm tọa độ véc-tơ

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a}$ =(1;1;0); $\vec{b}$ =(2;-1;-2); =(-3;0;2). Chọn mệnh đề đúng.

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC.

A. G(3;3;3)

B. G(1;1;1)

C. G(2/3;2/3;2/3)

D. G(1/3;1/3;1/3).

Xem lời giải »

Câu 21:

Cho =(2;0;1). Độ dài của véc-tơ bằng:

A. 5

B. 3

C. √5

D. √3

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, tìm tọa độ biết

A. =(5;-3;2)

B. =(2;-3;5)

C. =(2;5;-3)

D.=(-3;5;2)

Xem lời giải »

Câu 23:

Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ . Tìm tọa độ điểm A.

A. A(-2;3;0)

B. A(-2;0;3)

C. A(0;2;-3)

D. A(0;-2;3).

Xem lời giải »

Câu 24:

Trong không gian Oxyz cho $\vec{a} = (1; - 2; 3), \vec{b} = 2 \vec{i} - 3 \vec{k}$

Tọa độ của $\vec{a} + \vec{b}$ là

A. (3;-2;0)

B. (3;-5;-3)

C. (3;-5;0)

D. (1;2;-6).

Xem lời giải »

Câu 25:

Trong không gian với hệ trục tọa độ Oxyz, cho hai véc-tơ $\vec{a}$ = (1;-2;0) và $\vec{b}$ = (-2;3;1). Khẳng định nào sau đây là sai?

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(-4;4;6). Tọa độ trọng tâm G cảu tam giác OAB là:

A. G(1;-2;-3)

B. G(-1;2;3)

C. G(-3;6;9)

D. G(-3/2;3;9/2).

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho

Tọa độ của $\vec{u} = 2 \vec{a} - 3 \vec{b}$ là

Xem lời giải »

Câu 3:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:

A. H(0;-1;0)

B. H(0;-1;4)

C. H(2;-1;0)

D. H(2;0;4).

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho điểm A thỏa mãn . Khi đó tọa độ điểm A là:

A. (-2;3;7)

B. (2;-3;7)

C. (-3;2;7)

D. (2;7;-3).

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho hai điểm A(5;1;3), H(3;-3;-1). Tọa độ của điểm A' đối xứng với A qua H là:

A. (-1;7;5)

B. (1;7;5)

C. (1;-7;-5)

D. (1;-7;5).

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(5;7;2), B(3;0;4). Tọa độ của là:

A. =(2;7;-2)

B. =(2;7;2)

C. =(8;7;6)

D. =(-2;-7;2).

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho điểm M(-2; 5; 1). Khoảng cách từ M đến trục Ox bằng:

A. √29

B. 2

C. √5

D. √26

Xem lời giải »

Câu 8:

Trong không gian toạ độ Oxyz, cho điểm A(2;4;3). Khoảng cách từ điểm A đến mặt phẳng (Oyz) là:

A. 2

B. 4

C. 3

D. 5.

Xem lời giải »

Câu 9:

Trong không gian Oxyz, cho hai véc-tơ $\vec{a} = (2; 0; - 1) v à \vec{b} = (3; - 2; 1)$ . Tọa độ của vecto

Xem lời giải »

Câu 10:

Trong không gian Oxyz, cho hai véc-tơ $\vec{u} = (\sqrt{3}; 0; 1)$ và $\vec{v} = (0; \sqrt{3}; 1)$

Tọa độ vecto bằng:

A. 2

B. 1

C. - 3

D. 3.

Xem lời giải »

Câu 11:

Trong không gian Oxyz, cho điểm M(1;0;2). Mệnh nào sau đây đúng?

A. M ∈ (Oxz)

B. M ∈ (Oyz)

C. M ∈ Oy

D. M ∈ (Oxy).

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ $\vec{a} = (3; 2; 1) v à \vec{b} = (- 2; 0; 1)$

Tính $|\vec{a} + \vec{b}|$

A. 1

B. 2

C. 3

D. √2

Xem lời giải »

Câu 13:

Cho ba điểm A(2;1;4), B(2;2;-6), C(6;0;-1). Tích vô hướng của có giá trị bằng:

A. -51

B. 51

C. 55

D. 49.

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho hai điểm A(2;1;-1), B(1;2;3). Độ dài đoạn thẳng AB bằng:

A. √3

B. √22

C. 18

D. 3√2

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ

Xem lời giải »

Câu 16:

Trong không gian với hệ trục tọa độ Oxyz, cho hai véc-tơ . Khẳng định nào đúng?

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, tính độ dài đoạn AB với A(1;-1;0), B(2;0;-2).

A. AB = 2

B. AB = √2

C. AB = 6

D. AB = √6

Xem lời giải »

Câu 18:

#2H3Y1-2~Trong không gian với hệ tọa độ Oxyz, cho ba véc-tơ $\vec{a} = (- 1; 1; 0); \vec{b} = (1; 1; 0); \vec{c} = (1; 1; 1)$ . Trong các mệnh đề sau, mệnh đề nào sai?

A. $\vec{b} ⊥ \vec{c}$

B. $|\vec{c}| = \sqrt{3}$

C. $|\vec{a}| = \sqrt{2}$

D. $\vec{a} ⊥ \vec{b}$

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ $\vec{u} = (x; 2; 1) v à \vec{v} = (1; - 1; 2 x)$

Tính $\vec{u} . \vec{v}$

A. x + 2

B. 3x - 2

C. 3x + 2

D. -2 - x

Xem lời giải »

Câu 20:

#2H3Y1-2~Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;-2;3) và N(3;1;4). Tính độ dài véc-tơ

Xem lời giải »

Câu 21:

Cho ba điểm A(2; 1; 4), B(-2; 2; -6), C(6; 0; -1). Tích bằng:

A. -67

B. 65

C. 33

D. 67.

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ bất kỳ $\vec{a} = (x_{1}; y_{1}; z_{1}) v à \vec{b} = (x_{2}; y_{2}; z_{2})$ . Chọn khẳng định đúng.

Xem lời giải »

Câu 23:

#2H3Y1-2~Trong không gian với hệ toạ độ Oxyz, cho hai véc-tơ $\vec{a} = (2; - 2; - 4) v à \vec{b} = (1; - 1; 1)$ . Mệnh đề nào dưới đây sai?

A. $\vec{a} + \vec{b} = (3; - 3; - 3)$

B. $\vec{a} ⊥ \vec{b}$

C. $|\vec{b}| = \sqrt{3}$

D. $\vec{a} v à \vec{b}$ cùng phương

Xem lời giải »

Câu 24:

Trong không gian Oxyz, cho hai véc-tơ và . Tính :

A. (1;-3;4)

B. -8

C. -5

D. (1;-9;0).

Xem lời giải »

Câu 25:

#2H3Y1-2~Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(2;1;-2), N(4;-5;1). Tìm độ dài đoạn thẳng MN.

A. 49

B. 7

C. √7

D. √41

Xem lời giải »

Câu 1:

#2H3Y1-2~Trong không gian với hệ tọa độ số Oxyz cho các điểm A(1; 2; 3), B(2; 1; 5), C(2; 4; 2). Góc giữa hai đường thẳng AB và AC bằng:

A. 60⁰

B. 30⁰

C. 120⁰

D. 150⁰

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz cho $\vec{u} = (1; 0; 1) \vec{v} = (0; 1; - 2)$ là

Xem lời giải »

Câu 3:

Trong không gian Oxyz, cho đường thẳng d: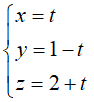. Đường thẳng d đi qua điểm nào sau đây:

A. K(1;-1;1)

B. F(0;1;2)

C. E(1;1;2)

D. H(1;2;0).

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x² + y² + z² - 2x + 4y - 6z + 9 =0. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).

A. I(-1;2;3), R=√5

B. I(1;-2;3), R=√5

C. I(1;-2;3), R=5

D. I(-1;2;-3), R=5.

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu tâm K(0;2;2√2) và tiếp xúc với mặt phẳng (Oxy) là:

A. x²+(y-2)²+(z-2√2)²=4

B. x²+(y-2)²+(z-2√2)²=8

C. x²+(y-2)²+(z-2√2)²=2√2

D. x²+(y-2)²+(z-2√2)²=2.

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) : x² + y² + z² - 2x + 4z + 1= 0. Tâm của mặt cầu là điểm:

A. I(1;-2;0)

B. I(1;0;-2)

C. I(-1;2;0)

D. I(0;1;2).

Xem lời giải »

Câu 7:

#2H3Y1-3~Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S): (x+1)²+(y-2)²+(z-1)²=9. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).

A. I(-1;2;1) và R=3

B. I(-1;2;1) và R=9

C. I(1;-2;-1) và R=3

D. I(1;-2;-1) và R=9.

Xem lời giải »

Câu 8:

#2H3Y1-3~Trong không gian Oxyz, phương trình mặt cầu (S) đường kính AB với A(4; -3; 5), B(2; 1; 3) là:

A. x² + y² + z² + 6x + 2y - 8z - 26 = 0

B. x² + y² + z² - 6x + 2y - 8z + 20 = 0

C. x² + y² + z² + 6x - 2y + 8z - 20 = 0

D. x² + y² + z² - 6x + 2y - 8z + 26 = 0.

Xem lời giải »

Câu 9:

#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz. Tìm tâm I và tính bán kính R của mặt cầu (S): x²+y²+z²-2x-4y+2z+2=0.

A. I(-1;-2;1),R=2

B. I(1;2;-1),R=2√2

C. I(-1;-2;1),R=2√2

D. I(1;2;-1),R=2.

Xem lời giải »

Câu 10:

#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-5)² + (y-1)² + (z+2)²=9. Tính bán kính R của mặt cầu (S).

A. R=18

B. R=9

C. R=3

D. R=6.

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-2=0. Tìm tọa độ tâm I và tính bán kính R của (S).

A. Tâm I(-1;2;-3) và bán kính R=4

B. Tâm I(1;-2;3) và bán kính R=4

C. Tâm I(-1;2;3) và bán kính R=4

D. Tâm I(1;-2;3) và bán kính R=16.

Xem lời giải »

Câu 12:

#2H3Y1-3~Trong không gian tọa độ Oxyz, xác định phương trình mặt cầu có tâm I(3;-1;2) và tiếp xúc mặt phẳng (P): x+2y-2z=0.

A. (x-3)²+(y+1)²+(z-2)²=2

B. (x-3)²+(y+1)²+(z-2)²=1

C. (x+3)²+(y-1)²+(z+2)²=1

D. (x+3)²+(y-1)²+(z+2)²=4.

Xem lời giải »

Câu 13:

#2H3Y1-3~Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+(y+2)²+z²=25. Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

A. I(1;-2;0), R=5

B. I(-1;2;0), R=25

C. I(1;-2;0), R=25

D. I(-1;2;0), R=5.

Xem lời giải »

Câu 14:

Trong không gian Oxyz, phương trình mặt cầu tâm I(2;1;-3) bán kính R=4 là:

A. (x+2)²+(y+1)²+(z-3)²=16

B. (x+2)²+(y+1)²+(z-3)²=4

C. (x-2)²+(y-1)²+(z+3)²=4

D. (x-2)²+(y-1)²+(z+3)²=16.

Xem lời giải »

Câu 15:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là x²+y²+z²-2x-4y-6z+5=0. Tính diện tích mặt cầu (S).

A. 42π

B. 36π

C. 9π

D. 12π.

Xem lời giải »

Câu 16:

#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình (x+1)²+(y-3)²+z²=16. Tìm tọa độ tâm I và bán kính R của mặt cầu đó.

A. I(-1;3;0), R=4

B. I(1;-3;0), R=4

C. I(-1;3;0), R=16

D. I(1;-3;0), R=16.

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S ): ( x-5 )²+( y-1 )²+( z+2 )²=16. Tính bán kính của (S).

A. 4

B. 16

C. 7

D. 5.

Xem lời giải »

Câu 18:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x-4y-6z-11=0. Toạ độ tâm T của (S) là:

A. T(1;2;3)

B. T(2;4;6)

C. T(-2;-4;-6)

D. T(-1;-2;-3)

Xem lời giải »

Câu 19:

Trong không gian Oxyz, mặt cầu tâm I(1;2;3) đi qua điểm A(1;1;2) có phương trình là:

A. (x-1)²+(y-1)²+(z-2)²=2

B. (x-1)²+(y-2)²+(z-3)²=2

C. (x-1)²+(y-2)²+(z-3)²=√2

D. (x-1)²+(y-1)²+(z-2)²=√2.

Xem lời giải »

Câu 20:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm I(1;0;-2) và mặt phẳng (P) có phương trình x + 2y -2z +4 =0. Phương trình mặt cầu (S) tâm I và tiếp xúc với mặt phẳng (P) là:

A. (x-1)² + y² + (z+2)² =9

B. (x-1)² +y² + (z+2)² =3

C. (x+1)² + y² + (z-2)² =3

D. (x+1)² + y² + (z-2)² =9.

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x²+y²+z²-x+2y+1=0. Tìm tọa độ tâm I và bán kính R của (S).

A. I(-1/2;1;0) và R = 1/4

B. I(1/2;1;0) và R = 1/2

C. I(1/2;-1;0) và R = 1/2

D. I(-1/2;1;0) và R = 1/2

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho mặt cầu (S): x²+y²+z²-2x+6y-6=0. Bán kính của (S) bằng:

A. √46

B. 16

C. 2

D. 4.

Xem lời giải »

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x-2y-2z+3=0. Tính khoảng cách d từ điểm M(2;1;0) đến mặt phẳng (P).

A. d = 1/3

B. d = √3/3

C. d = 3

D. d = 1

Xem lời giải »

Câu 24:

#2H3Y2-1~Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;3;2), B(2;-1;5) và C(3;2;-1). Gọi là tích có hướng của hai véc-tơ . Tìm tọa độ véc-tơ .

A. = (15;9;7)

B. = (9;3;-9).

C. = (3;-9;9)}

D. = (9;7;15)}

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P:3x-4y+5z-2=0. Véc-tơ nào dưới đây là một véc-tơ pháp tuyến của mặt phẳng P?

A. =(3;-5;-2)

B. =(-4;5;-2)

C. =(3;-4;5)

D. =(3;-4;2).

Xem lời giải »

Câu 1:

Trong không gian Oxyz, cho mặt phẳng (P) có phương trình -x+2y+3z-4=0. Mặt phẳng (P) có một véc-tơ pháp tuyến là:

A. = (-1;3;4)

B. = (2;3;-4)

C. = (-1;2;3)

D. = (-1;2;-4).

Xem lời giải »

Câu 2:

Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng qua A(1;2;-1) có một véc-tơ pháp tuyến = (2;0;0) có phương trình là:

A. y + z = 0

B. y + z - 1 = 0

C. x - 1 = 0

D. 2x - 1 = 0.

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, véc-tơ nào dưới đây là một véc-tơ pháp tuyến của mặt phẳng (Oxy)?

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz, cho M(1;-1;2), N(3;1;-4). Viết phương trình mặt phẳng trung trực của MN.

A. x + y + 3z + 5 = 0

B. x + y - 3z - 5 = 0

C. x + y + 3z + 1 = 0

D. x + y - 3z + 5 = 0.

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxy, cho hai điểm A(2;3;1), B(0;1;2). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:

A. (P): 2x + 2y - z = 0

B. (P): 2x + 2y - z - 9 = 0

C. (P): 2x + 4y + 3z - 19 = 0

D. (P): 2x + 4y + 3z - 10 = 0.

Xem lời giải »

Câu 6:

Trong không gian với hệ toạ độ Oxyz, cho 3 điểm M(3;0;0), N(0;-2;0), P(0;0;1). Mặt phẳng (MNP) có phương trình:

Xem lời giải »

Câu 7:

Trong không gian Oxyz, mặt phẳng (Oxy) có phương trình là:

A. z = 0

B. x + y + z = 0

C. y = 0

D. x = 0.

Xem lời giải »

Câu 8:

Trong không gian với hệ toạ độ Oxyz, phương trình nào sau đây là phương trình của mặt phẳng Oxz?

A. y = 0

B. x = 0

C. z = 0

D. y - 1 = 0.

Xem lời giải »

Câu 9:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(-2;0;0), B(0;3;0) và C(0;0;2). Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?

Xem lời giải »

Câu 10:

Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(2; -1; 1),B(1; 0;4) và C(0; -2; -1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là:

A. 2x + y + 2z - 5 = 0

B. x + 2y + 5z + 5 = 0

C. x - 2y + 3z - 7 = 0

D. x + 2y + 5z - 5 = 0.

Xem lời giải »

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(2; -1; 0) và mặt phẳng (P): x - 2y - 3z + 10 = 0. Phương trình mặt phẳng (Q) đi qua A và song song với mặt phẳng (P) là:

A. x - 2y + 3z + 4 = 0

B. -x + 2y + 3z + 4 = 0

C. x - 2y - 3z + 4 = 0

D. x + 2y - 3z = 0.

Xem lời giải »

Câu 12:

Trong hệ tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;3) và có véc-tơ pháp tuyến là:

A. -2x + z + 1 = 0

B. -2y + z - 1 = 0

C. -2x + z - 1 = 0

D. -2x + y - 1 = 0.

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho ba điểm A(4;3;2), B(-1;-2;1) và C(-2;2;-1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:

A. x - 4y + 2z + 4 = 0

B. x - 4y - 2z + 4 = 0

C. x - 4y - 2z - 4 = 0

D. x + 4y - 2z - 4 = 0.

Xem lời giải »

Câu 14:

Trong không gian Oxyz, phương trình mặt phẳng qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;1) được viết dưới dạng ax + by -6z + c=0. Giá trị của T=a+b-c là:

A. -11

B. -7

C. -1

D. 11.

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;4;-2) và =(-2;3;-4). Phương trình mặt phẳng (P) đi qua điểm A và nhận làm véc-tơ pháp tuyến là:

A. -3x + 4y - 2z + 26 = 0

B. -2x + 3y - 4z + 29 = 0

C. 2x - 3y + 4z + 29 = 0

D. 2x - 3y + 4z + 26 = 0.

Xem lời giải »

Câu 16:

Trong không gian Oxyz, tìm phương trình mặt phẳng (α) cắt ba trục Ox, Oy, Oz lần lượt tại ba điểm A(-3;0;0), B(0;4;0), C(0;0;-2).

A. 4x + 3y - 6z + 12 = 0

B. 4x + 3y + 6z + 12 = 0

C. 4x - 3y + 6z + 12 = 0

D. 4x - 3y + 6z - 12 = 0.

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến =(2; 3; 5). Phương trình mặt phẳng (α) là:

A. 2x + 3y + 5z - 16=0

B. x - 2y + 4z - 16=0

C. 2x + 3y + 5z + 16=0

D. x - 2y + 4z=0.

Xem lời giải »

Câu 18:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) đi qua điểm G(1;1;1) và vuông góc với đường thẳng OG có phương trình là:

A. x + y + z - 3 = 0

B. x - y + z = 0

C. x + y - z - 3 = 0

D. x + y + z = 0.

Xem lời giải »

Câu 19:

Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (P) đi qua gốc toạ độ và nhận =(3;2;1) là véctơ pháp tuyến. Phương trình của mặt phẳng (P) là:

A. 3x + 2y + z - 14 = 0

B. 3x + 2y + z = 0

C. 3x + 2y + z + 2 = 0

D. x + 2y + 3z = 0.

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng (Oxz) là:

A. x=0

B. x+z=0

C. z=0

D. y=0.

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng(α) đi qua điểm M(1;2;-3) và nhận =(1;-2;3) làm véc-tơ pháp tuyến có phương trình là:

A. x - 2y - 3z + 6 = 0

B. x - 2y - 3z - 6 = 0

C. x - 2y + 3z - 12 = 0

D. x - 2y + 3z + 12 = 0.

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P):2x + 3y + 4z - 12 = 0 cắt trục Oy tại điểm có tọa độ là:

A. (0;4;0)

B. (0;6;0)

C. (0;3;0)

D. (0;-4;0).

Xem lời giải »

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - y - 2z - 3 = 0. Điểm nào dưới đây thuộc mặt phẳng (P)?

A. M(2; -1; -3)

B. Q(3; -1; 2)

C. P(2; -1; -1)

D. N(2; -1; -2).

Xem lời giải »

Câu 24:

Trong không gian Oxyz, cho mặt phẳng (P): 3x + 2y - z + 1 = 0. Điểm nào dưới đây thuộc (P) ?

A. N(0;0;-1)

B. M(-10;15;-1)

C. E(1;0;-4)

D. F(-1;-2;-6).

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): x + y + z - 6 = 0. Điểm nào dưới đây không thuộc mặt phẳng (α)?

A. M(1; -1; 1)

B. Q(3; 3; 0)

C. N(2; 2; 2)

D. P(1; 2; 3).

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:

A. H(2;0;4)

B. H(0;-1;4)

C. H(2;-1;0)

D. H(0;-1;0).

Xem lời giải »

Câu 2:

Trong không gian với hệ trục toạ độ Oxyz, cho mặt phẳng (α): 2x - 3y - z - 1 = 0. Điểm nào dưới đây không thuộc mặt phẳng (α)?

A. Q(1;2;-5)

B. P(3;1;3)

C. M(-2;1;-8)

D. N(4;2;1).

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 3x - 2y + z - 5 = 0. Điểm nào dưới đây thuộc mặt phẳng (P)?

A. N(3;-2;-5)

B. P(0;0;-5)

C. Q(3;-2;1)

D. M(1;1;4).

Xem lời giải »

Câu 4:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;3). Tọa độ điểm A là hình chiếu vuông góc của điểm M lên mặt phẳng (Oyz) là:

A. A(1;-2;0)

B. A(0;-2;3)

C. A(1;-2;3)

D. A(1;0;3).

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 5z - 4 = 0. Điểm nào sau đây thuộc mặt phẳng (P) ?

A. A(11; 2; 3)

B. B(-5; 2; -3)

C. C(5; 2; -1)

D. D(-5;-2;1)

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, tính thể tích tứ diện OABC, biết A, B, C lần lượt là giao điểm của mặt phẳng 2x - 3y + 4z + 24 = 0 với trục Ox, Oy, Oz.

A. 192

B. 288

C. 96

D. 78.

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho điểm M(a;b;1) thuộc mặt phẳng (P): 2x - y + z - 3 = 0. Mệnh đề nào dưới đây đúng?

A. 2a - b = 3

B. 2a - b = 2

C. 2a - b = -2

D. 2a - b = 4.

Xem lời giải »

Câu 8:

Góc giữa 2 mặt phẳng (P): 8x - 4y -8z-11 = 0 và (Q): √2x - √2y + 7 = 0 bằng:

A. 90⁰

B. 30⁰

C. 45⁰

D. 60⁰.

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho (P): 3x-4y+2z+4=0 và điểm A(1;-2;3). Tính khoảng cách từ A đến (P).

Xem lời giải »

Câu 10:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 3x+4y+2z+4=0 và điểm A(1;-2;3). Tính khoảng cách d từ A đến mặt phẳng (P).

A. d = √5/3

B. d = 5/9

C. d = 5/29

D. d = 5/√29

Xem lời giải »

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+y-2z-6=0. Tính khoảng cách từ O đến (P).

A. 3

B. 2/3

C. -2

D. 2.

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(-1;2;-5). Tính khoảng cách từ điểm M đến mặt phẳng (Oxy).

A. √30

B. √5

C. 25

D. 5

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho mặt phẳng (P): 2x - 2y + z + 5 = 0. Tính khoảng cách từ điểm M(-1; 2; -3) đến mặt phẳng (P).

A. 4/3

B. - 4/3

C. 2/3

D. 2/9

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho ba điểm A(1;0;0), B(0;-1;0) và C(0;0;2). Khoảng cách từ gốc tọa độ đến mặt phẳng (ABC) bằng:

A. 2/3

B. 2

Xem lời giải »

Câu 15:

Cho điểm H(-3;-4;6) và mặt phẳng (Oxz). Hỏi khoảng cách từ điểm H đến mặt phẳng (Oxz) bằng bao nhiêu?

A. d(H;(Oxz))=4

B. d(H;(Oxz))=3

C. d(H;(Oxz))=6

D. d(H;(Oxz))=8.

Xem lời giải »

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; -2; -1), B(1; 4; 3). Độ dài của đoạn AB là:

A. 3

B. √6

C. 2√3

D. 2√13

Xem lời giải »

Câu 17:

Lập phương trình của mặt phẳng đi qua A(2;6;-3) và song song với mặt phẳng (Oyz).

A. x=2

B. x+z=12

C. y=6

D. z=-3.

Xem lời giải »

Câu 18:

Trong không gian Oxyz, phương trình mặt phẳng tiếp xúc với mặt cầu(S): (x-1)² + (y-2)² + (z-3)²=81 tại điểm P(-5;-4;6) là:

A. 7 x + 8y + 67 = 0

B. 4 x + 2y - 9z + 82 = 0

C. x - 4z + 29 = 0

D. 2x + 2y - z + 24 = 0

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): x+2y-z-1=0 và (β): 2x+4y-mz-2=0. Tìm m để hai mặt phẳng (α) và (β) song song với nhau.

A. m=1

B. Không tồn tại m

C. m=-2

D. m=2.

Xem lời giải »

Câu 20:

Trong không gian Oxyz, cho mặt cầu (S) tâm O(0;0;0) và tiếp xúc với mặt phẳng(α): 2x+y+2z-6=0. Tính bán kính của (S).

A. 1

B. 3

C. 2

D. 6.

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x=1-2t ; y=1+t; z=t+2 (t ∈ R). Tìm một véc-tơ chỉ phương của đường thẳng d.

A. (-2;1;2)

B. (-2;1;1)

C. (1;1;1)

D. (2;-1;-2).

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho mặt phẳng (P): x-2y-3z-2=0. Đường thẳng d vuông góc với mặt phẳng (P) có một véc-tơ chỉ phương có tọa độ là:

A. (1;-2;2)

B. (1;-2;-3)

C. (1;2;3)

D. (1;-3;-2).

Xem lời giải »

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có véc-tơ chỉ phương $\vec{u}$ và mặt phẳng (P) có véc-tơ pháp tuyến $\vec{n}$ . Mệnh đề nào dưới đây đúng?

A. $\vec{u}$ vuông góc với $\vec{n}$ thì d song song với (P)

B. $\vec{u}$ không vuông góc với $\vec{n}$ thì d cắt (P)

C. d song song với (P) thì $\vec{u}$ cùng phương với $\vec{n}$

D. d vuông góc với (P) thì $\vec{u}$ vuông góc với $\vec{n}$

Xem lời giải »

Câu 24:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;-1;-2) và B(2;2;2). Véc-tơ nào dưới đây là một véc-tơ chỉ phương của đường thẳng AB?

A. =(2;1;0)

B. =(2;3;4)

C. =(-2;1;0)

D. =(2;3;0).

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, véc-tơ nào dưới đây là một véc-tơ chỉ phương của Oz?

Xem lời giải »

Câu 1:

Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.

A. 6x + 3y - 2z - 6 = 0

B. x + 2y + 3z - 14 = 0

C. x + 3y + 2z - 11 = 0

$D . \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 3$

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA²+ 2MB²- MC² đạt giá trị nhỏ nhất.

$A . M (\frac{3}{4}; \frac{1}{2}; - 1)$

$B . M (- \frac{3}{4}; \frac{1}{2}; 2)$

$C . M (- \frac{3}{4}; \frac{3}{2}; - 1)$

$D . M (- \frac{3}{4}; \frac{1}{2}; - 1)$

Xem lời giải »

Câu 3:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?

A. a + b + c = 12

B. a² + b = c - 6

C. a + b + c = 18

D. a + b - c = 0

Xem lời giải »

Câu 4:

Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).

A. arccos(4/15)

B. 1

C. arcsin(4/5)

D. arccos(4/5)

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:

A. 2x + y + z - 6 = 0

B. x + 2y + z - 6 = 0

C. x + 2y + 2z - 6 = 0

D. 2x + y + z + 6 = 0

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 0; -2), B(4; 0; 0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:

A. I (0;0;-1)

B. I (2;0;0)

C. I (2;0;-1)

D. I (4/3;0;-2/3)

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;-3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho $|\vec{M A} + \vec{M B} - \vec{M C}|$ nhỏ nhất.

A. M (3;3;-3)

B. M (-3;-3;3)

C. M (3;-3;3)

D. M (-3;3;3)

Xem lời giải »

Câu 8:

Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng $d : \{\begin{matrix} x = t \\ y = t \\ z = 1 + t \end{matrix}\}$

Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.

A. 2x + y - 3z + 3 = 0

B. x + 2y - z - 1 = 0

C. 3x + 2y - z + 1 = 0

D. 2x - y - 3z + 3 = 0

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x + 1}{2} = \frac{y + 1}{1} = \frac{z + 1}{3}$ và $d_{2} = \frac{x - 2}{1} = \frac{y}{2} = \frac{z - 9}{3}$

Mặt cầu có một đường kính là đoạn thẳng vuông góc chung của d₁ và d₂ có phương trình là:

Xem lời giải »

Câu 10:

Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.

A. 4a/3

B. a/3

C. 2a/3

D. 3a/4

Xem lời giải »

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức $|\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D}|$ đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:

A. M (0;1;-4)

B. M (2;1;0)

C. M (0;1;-2)

D. M (0;1;4)

Xem lời giải »

Câu 12:

Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.

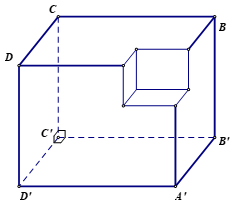
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.

$A . \frac{2 + \sqrt{3}}{3}$

$B . 3 - \sqrt{3}$

$C . \frac{2 \sqrt{3}}{3}$

$D . \sqrt{2}$

Xem lời giải »

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC

A. 1372/9

B. 686/9

C. 524/3

D. 343/9

Xem lời giải »

Câu 14:

Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB = 2a, AD = a. Gọi K là điểm thuộc BC sao cho $3 \vec{B K} + 2 \vec{C K} = \vec{0}$ . Tính khoảng cách giữa hai đường thẳng AD và SK.

$A . x = \frac{2 \sqrt{165} a}{15}$

$B . x = \frac{\sqrt{165} a}{15}$

$C . x = \frac{2 \sqrt{135} a}{15}$

$D . x = \frac{\sqrt{135} a}{15}$

Xem lời giải »

Câu 15:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức AM²+ BM² = 30 là một mặt cầu (S). Tọa độ tâm I và bán kính R của mặt cầu (S) là:

$A . I (- 2; - 2; - 8); R = 3$

$B . I (- 1; - 1; - 4); R = \sqrt{6}$

$C . I (- 1; - 1; - 4); R = 3$

$D . I (- 1; - 1; - 4); R = \frac{\sqrt{30}}{2}$

Xem lời giải »

Câu 16:

Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1;0;0), B(0;1;0), C(0;0;1), D(0;0;0). Hỏi có bao nhiêu điểm cách đều 4 mặt phẳng (ABC), (CDA), (BCD), (DAB).

A. 4

B. 5

C. 1

D. 8

Xem lời giải »

Câu 17:

Trong không gian Oxyz, cho tứ diện S.ABC có S(0;0;1), A(1;0;1), B(0;1;1), C (0;0;2). Hỏi tứ diện S.ABC có bao nhiêu mặt phẳng đối xứng?

A. 6

B. 1

C. 0

D. 3

Xem lời giải »

Câu 18:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: $x^{2} + y^{2} + z^{2} - 2 x - 2 y - 6 z + 7 = 0$ .

Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = $90 °$ . Diện tích tam giác AMB có giá trị lớn nhất bằng?

A. 4

B. 2

C. 4π

D. Không tồn tại.

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2;1;3), B(1;-1;2), C(3;-6;1). Điểm M(x;y;z) thuộc mặt phẳng (Oyz) sao cho MA²+ MB²+ MC² đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x+y+z

A. P = 0

B. P = 2P = 0

C. P = 6

D. P = -2

Xem lời giải »

Câu 20:

Trong không gian với hệ trục tọa độ Oxyz cho hình thang ABCD vuông tại A và B. Ba đỉnh A(1;2;1), B(2;0;-1), C(6;1;0). Hình thang có diện tích bằng 6√2. Giả sử đỉnh D(a;b;c), tìm mệnh đề đúng?

A. a+b+c=6

B. a+b+c=5

C. a+b+c=8

D. a+b+c=7

Xem lời giải »

Câu 21:

Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.

$A . x = \frac{a \sqrt{2}}{3}$

$B . x = \frac{a \sqrt{2}}{4}$

$C . x = \frac{a}{3}$

$D . x = \frac{a}{2}$

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?

A. Có vô số mặt phẳng.

B. 1 mặt phẳng.

C. 7 mặt phẳng.

D. 4 mặt phẳng.

Xem lời giải »

Câu 23:

Trong không gian Oxyz, cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của đường thẳng d là:

Xem lời giải »

Câu 24:

Trong không gian Oxyz, cho hai điểm A(-1;2;1), B(1;2;-3) và đường thẳng d: $\frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ . Tìm vectơ chỉ phương $\vec{u}$ của đường thẳng Δ đi qua điểm A và vuông góc với d đồng thời cách B một khoảng lớn nhất.

$A . \vec{u} = (4; - 3; 2)$

$B . \vec{u} = (2; 0; - 4)$

$C . \vec{u} = (2; 2; - 1)$

$D . \vec{u} = (1; 0; 2)$

Xem lời giải »

Câu 25:

Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:

A. (x + 2)²+ (y - 2)² + (z + 1)² = 9 và (x + 1)² + (y - 2)² + (z + 2)² = 9

B. (x - 2)²+ (y - 2)² + (z - 1)² = 9 và x² + y² + (z + 3)² = 9

C. (x + 2)²+ (y - 2)² + (z + 1)² = 9 và (x + 1)² + (y - 2)² + (z + 2)² = 9

D. (x + 1)²+ (y - 2)² + (z + 2)² = 9 và (x - 2)² + (y - 2)² + (z - 1)² = 9

Xem lời giải »

Câu 1:

Trong không gian Oxyz, cho hai điểm M(0;1;3), N(10;6;0) và mặt phẳng (P): x - 2y + 2z -10 = 0. Điểm I(-10; a; b) thuộc mặt phẳng (P) sao cho |IM - IN| lớn nhất. Khi đó tổng T = a + b bằng:

A. T = 5

B. T = 1

C. T = 2

D. T = 6

Xem lời giải »

Câu 2:

Trong không gian tọa độ Oxyz, cho mặt cầu (S): x²+ y² + z² - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:

A. r = $\sqrt{6}$

B. r = 2 $\sqrt{2}$

C. r = 4

D. r = 2 $\sqrt{3}$

Xem lời giải »

Câu 3:

Trong không gian tọa độ Oxyz cho mặt cầu (S): x²+ y²+ z²+ 4x - 6y + m = 0 và đường thẳng Δ là giao tuyến của hai mặt phẳng (α): x + 2y - 2z - 4 = 0 và (β): 2x - 2y - z + 1 = 0. Đường thẳng Δ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn AB = 8 khi:

A. m = 12

B. m = -12

C. m = -10

D. m = 5

Xem lời giải »

Câu 4:

Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân tại A, cạnh BC = a√6. Góc giữa mặt phẳng (AB'C) và mặt phẳng (BCC'B') bằng 60⁰. Tính thể tích V của khối lăng trụ ABC.A'B'C'?

$A . V = \frac{2 a^{3} \sqrt{3}}{3}$

$B . V = \frac{a^{3} \sqrt{3}}{2}$

$C . V = \frac{3 a^{3} \sqrt{3}}{4}$

$D . V = \frac{3 a^{3} \sqrt{3}}{2}$

Xem lời giải »

Câu 5:

Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S).

A. $(S) : x^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 3$

B. $(S) : x^{2} + {(y + 2)}^{2} + {(z + 1)}^{2} = 1$

C . $(S) : x^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 3$

D. $(S) : x^{2} + {(y + 2)}^{2} + {(z + 1)}^{2} = 2$

Xem lời giải »

Câu 6:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (1;1;1). Mặt phẳng (P) đi qua M và cắt chiều dương của các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C thỏa mãn OA = 2OB. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC.

A. 64/27

B. 10/3

C. 9/2

D. 81/16

Xem lời giải »

Câu 7:

Trong không gian với hệ trục tọa độ Oxyz cho hai mặt cầu:

$(S_{1}) : x^{2} + y^{2} + z^{2} + 4 x + 2 y + z = 0$ ;

$(S_{2}); x^{2} + y^{2} + z^{2} - 2 x - y - z = 0$

cắt nhau theo một đường tròn (C) nằm trong mặt phẳng (P). Cho các điểm A (1; 0; 0), B (0; 2; 0), C (0; 0; 3). Có bao nhiêu mặt cầu tâm thuộc (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA?

A. 4 Mặt cầu.

B. 2 Mặt cầu.

C. 3 Mặt cầu.

D. 1 Mặt cầu.

Xem lời giải »

Câu 8:

Trong không gian với hệ tọa độ Oxyz cho điểm A (2;1;2) và mặt cầu (S): x²+ y²+ z²- 2y - 2z - 7 = 0. Mặt phẳng (P) đi qua A và cắt (S) theo thiết diện là đường tròn (C) có diện tích nhỏ nhất. Bán kính đường tròn (C) là:

A. 1

B. $\sqrt{5}$

C. 3

D. 2

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz cho A (1; 2; -3), B (3/2; 3/2; -1/2), C (1; 1; 4), D (5; 3; 0). Gọi (S₁) là mặt cầu tâm A bán kính bằng 3, (S₂) là mặt cầu tâm B bán kính bằng 3/2. Có bao nhiêu mặt phẳng tiếp xúc với 2 mặt cầu (S₁), (S₂) đồng thời song song với đường thẳng đi qua 2 điểm C, D.

A. 1

B. 2

C. 4

D. Vô số.

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (2; -3; 7), B (0; 4; -3) và C (4; 2; 5). Biết điểm $M (x_{0}; y_{0}; z_{0})$ nằm trên (Oxy) sao cho $|\vec{M A} + \vec{M B} + \vec{M C}|$ có giá trị nhỏ nhất. Khi đó tổng $P = x_{0} + y_{0} + z_{0}$ bằng:

A. P = 0

B. P = 6

C. P = 3

D. P = -3

Xem lời giải »

Câu 11:

Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.

A. $r = \sqrt{3}$

B. $r = \sqrt{\frac{3}{2}}$

C. $r = \sqrt{2}$

D. $r = \frac{3 \sqrt{2}}{2}$

Xem lời giải »

Câu 12:

Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 6 y - 4 z - 2 = 0$ ,mặt phẳng $(α) : x + 4 y + z - 11 = 0$ .Gọi (P) là mặt phẳng vuông góc với $(α)$ , (P) song song với giá của véctơ $\vec{v} = (1; 6; 2)$ và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P)

A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0.

B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0.

C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0.

D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0.

Xem lời giải »

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 16$ và các điểm A (1; 0; 2), B (-1; 2; 2). Gọi (P) là mặt phẳng đi qua hai điểm A, B sao cho thiết diện của (P) với mặt cầu (S) có diện tích nhỏ nhất.Khi viết phương trình (P) dưới dạng (P): ax + by + cz + 3 = 0. Tính T = a + b + c

A. 3

B. -3

C. 0

D. -2

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho tứ diện OABC (O là gốc tọa độ), A ∈ Ox, B ∈ Oy, C ∈ Oz và mặt phẳng (ABC) có phương trình: 6x + 3y + 2z - 12 = 0. Thể tích khối tứ diện OABC bằng:

A. 14

B. 3

C. 1

D. 8

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1; 0; 0), B (0; 0; 2) và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 2 y + 1 = 0$ . Số mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S) là:

A. 1 mặt phẳng

B. 2 mặt phẳng

C. 3 mặt phẳng

D. Vô số mặt phẳng.

Xem lời giải »

Câu 16:

Trong không gian Oxyz cho điểm M (3; 2; 1). Viết phương trình mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC.

A. 3x + y + 2z - 14 = 0

B. 3x + 2y + z - 14 = 0

$C . \frac{x}{9} + \frac{y}{3} + \frac{z}{6} = 1$

$D . \frac{x}{12} + \frac{y}{4} + \frac{z}{4} = 1$

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz cho A (3;2;1), B (-2;3;6). Điểm M (x_M; y_M; z_M) thay đổi thuộc mặt phẳng (Oxy). Tìm giá trị của biểu thức T = x_M+ y_M+ z_M khi $|\vec{M A} + 3 \vec{M B}|$ nhỏ nhất.

A. -7/2

B. 7/2

C. 2

D. -2

Xem lời giải »

Câu 18:

Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A (1; 1; 1), B (0; 1; 2), C (-2; 1; 4) và mặt phẳng (P): x - y + z + 2 = 0. Tìm điểm N ∈ (P) sao cho S = 2NA²+ NB²+ NC² đạt giá trị nhỏ nhất.

$A . N (- \frac{4}{3}; 2; \frac{4}{3})$

B. N (-2; 0; 1)

$C . N (- \frac{1}{2}; \frac{5}{4}; \frac{3}{4})$

D. N (-1; 2; 1)

Xem lời giải »

Câu 19:

Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (3; 4; 4), C (2; 6; 6) và I (a; b; c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + b + c.

A. 63/5

B. 31/3

C. 46/5

D. 10

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2; 0; 0); B (0; 3; 0); C (0; 0 ;4). Gọi H là trực tâm tam giác ABC. Tìm phương trình tham số của đường thẳng OH.

$A . \{\begin{matrix} x = 4 t \\ y = 3 t \\ z = - 2 t \end{matrix}$

$B . \{\begin{matrix} x = 3 t \\ y = 4 t \\ z = 2 t \end{matrix}$

$C . \{\begin{matrix} x = 6 t \\ y = 4 t \\ z = 3 t \end{matrix}$

$D . \{\begin{matrix} x = 4 t \\ y = 3 t \\ z = 2 t \end{matrix}$

Xem lời giải »

Câu 21:

Cho a, b, c, d, e, f là các số thực thỏa mãn

$\{\begin{cases} {(d - 1)}^{2} + {(e - 2)}^{2} + {(f - 3)}^{2} = 1 \\ {(a + 3)}^{2} + {(b - 2)}^{2} + c^{2} = 9 \end{cases}$

Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức $F = \sqrt{{(a - d)}^{2} + {(b - e)}^{2} + {(c - f)}^{2}}$ lần lượt là M, m

Khi đó, M - m bằng:

A. 10

B. $\sqrt{10}$

C. 8

D. 2 $\sqrt{2}$

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?

$A . d = - \frac{\sqrt{3}}{3}$

$B . d = \sqrt{3}$

$C . d = \frac{1}{3}$

$D . d = \frac{1}{\sqrt{3}}$

Xem lời giải »

Câu 23:

Trong không gian với hệ trục tọa độ , cho bốn đường thẳng:

$d_{1} : \frac{x - 3}{1} = \frac{y + 1}{- 2} = \frac{z + 1}{1}; d_{2} : \frac{x}{1} = \frac{y}{- 2} = \frac{z - 1}{1}$

$d_{3} : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 1}{1}; d_{4} : \frac{x}{1} = \frac{y - 1}{- 1} = \frac{z}{- 1}$

Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:

A. 0

B. 2

C. Vô số.

D. $1$

Xem lời giải »

Câu 24:

Trong không gian với hệ tọa độ Oxyz, cho M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 = 0. Hình chiếu vuông góc của M lên mặt phẳng (P) là:

A. H (2; 5; 3)

B. H (2; -3; 1)

C. H (6; 7; 3)

D. H (1; 5; 2)

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - 2y + z -1 = 0 và điểm A (0; -2; 3), B (2; 0; 1). Điểm M (a; b; c) thuộc (P) sao cho MA + MB nhỏ nhất.

Giá trị của a²+ b²+ c² bằng:

A. 41/4

B. 9/4

C. 7/4

D. 3

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (1; 1; 2), B (-1; 0; 4), C (0; -1; 3) và điểm M thuộc mặt cầu (S): x²+ y²+ (z - 1)²= 1. Khi biểu thức MA²+ MB²+ MC² đạt giá trị nhỏ nhất thì độ đài đoạn AM bằng:

A. $\sqrt{2}$

B. $\sqrt{6}$

C. 6

D. 2

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho hai điểm A (1; 2; 1), B (2; -1; 3). Tìm điểm M trên mặt phẳng (Oxy) sao cho $M A^{2} - 2 M B^{2}$ lớn nhất.

$A . M (\frac{3}{2}; \frac{1}{2}; 0)$

$B . M (\frac{1}{2}; - \frac{3}{2}; 0)$

C. M (0; 0; 5)

D. M (3; -4; 0)

Xem lời giải »

Câu 3:

Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh bên bằng cạnh đáy. Đường thẳng MN (M ∈ A'C, N ∈ BC') là đường vuông góc chung của A'C và BC'. Tỷ số NB/NC' bằng:

A. $\sqrt{5} / 2$

B. 3/2

C. 2/3

D. 1

Xem lời giải »

Câu 4:

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x + y -2z + m = 0 và mặt cầu (S): x²+ y²+ z²- 2x + 4y -6z - 2= 0. Có bao nhiêu giá trị nguyên của m để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3

A. 3

B. 4

C. 2

D. 1

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho hai điểm A (0; 8; 2), B (9; -7; 23) và mặt cầu (S) có phương trình (S): (x - 5)²+ ( $y + 3$ )²+ (z - 7)²= 72. Mặt phẳng (P): x + by + cz + d = 0 đi qua điểm A và tiếp xúc với mặt cầu (S) sao cho khoảng cách từ B đến mặt phẳng (P) lớn nhất. Giá trị của b + c + d khi đó là

A. b + c + d = 2

B. b + c + d = 4

C. b + c + d = 3

D. b + c + d = 1

Xem lời giải »

Câu 6:

Trong không gian với hệ trục Oxyz, cho hai điểm M (1; 2; 1); N (-1; 0; -1). Có bao nhiêu mặt phẳng (P) qua M, N cắt trục Ox, trục Oy lần lượt tại A, B (A ≠ B) sao cho AM = √3BN

A. 1

B. 2

C. 3

D. Vô số.

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:

A. 6 $\sqrt{3}$

B. 12 $\sqrt{3}$

C. $\frac{5 \sqrt{3}}{2}$

D. 5 $\sqrt{3}$

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x + 1}{1} = \frac{y + 3}{2} = \frac{z + 2}{2}$ và điểm A(3;2;0). Điểm đối xứng của điểm A qua đường thẳng d có tọa độ là:

A. (-1; 0; 4)

B. (7; 1; -1)

C. (2; 1; -2)

D. (0; 2; -5)

Xem lời giải »

Câu 9:

Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (1; 0; -1), C (2; -1; 2). Điểm D thuộc tia Oz sao cho độ dài đường cao xuất phát từ đỉnh D của tứ diện ABCD bằng $\frac{3 \sqrt{30}}{10}$ có tọa độ là:

A. (0; 0 ; 1)

B. (0; 0 ; 3)

C. (0; 0 ; 2)

D. (0; 0 ; 4)

Xem lời giải »

Câu 10:

Trong không gian Oxyz, cho ba điểm A (-1; 0; 1), B (3; 2; 1), C (5; 3; 7). Gọi M (a; b; c) là điểm thỏa mãn MA = MB và MB + MC đạt giá trị nhỏ nhất. Tính P = a + b + c

A. P = 4

B. P = 0

C. P = 2

D. P = 5

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x + 1}{2} = \frac{y}{1} = \frac{z - 2}{1}$ , mặt phẳng (P): x + y - 2z + 5 = 0 và A (1; -1; 2). Đường thẳng Δ cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vectơ chỉ phương của Δ là:

$A . \vec{u} = (2; 3; 2)$

$B . \vec{u} = (1; - 1; 2)$

$C . \vec{u} = (- 3; 5; 1)$

$D . \vec{u} = (4; 5; - 13)$

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (0; 2; 2), B (2; -2; 0). Gọi I₁ (1; 1; -1) và I₂ (3; 1; 1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S).

$A . R = \frac{\sqrt{219}}{3}$

B. R = 2 $\sqrt{2}$

$C . R = \frac{\sqrt{129}}{3}$

D. R = 2 $\sqrt{6}$

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho ba đường thẳng $d_{1} : \frac{x - 3}{2} = \frac{y + 1}{1} = \frac{z - 2}{- 2}$ , $d_{2} : \frac{x + 1}{3} = \frac{y}{- 2} = \frac{z + 4}{- 1}$ và $d_{3} : \frac{x + 3}{4} = \frac{y - 2}{- 1} = \frac{z}{6}$ .Đường thẳng song song d₃, cắt d₂ và d₁ có phương trình là:

$A . \frac{x - 3}{4} = \frac{y + 1}{1} = \frac{z - 2}{6}$

$B . \frac{x - 3}{- 4} = \frac{y + 1}{1} = \frac{z - 2}{- 6}$

$C . \frac{x + 1}{4} = \frac{y}{- 1} = \frac{z - 4}{6}$

$D . \frac{x - 1}{4} = \frac{y}{- 1} = \frac{z + 4}{6}$

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho ba điểm A (3; 0; 0), B (1; 2; 1) và C (2; -1; 2). Biết mặt phẳng qua B, C và tâm mặt cầu nội tiếp tứ diện OABC có một vectơ pháp tuyến là (10; a; b). Tổng a + b là:

A. -2

B. 2

C. 1

D. -1

Xem lời giải »

Câu 15:

Trong không gian Oxyz cho hai đường thẳng $∆_{1} : \{\begin{matrix} x = 1 \\ y = 2 + t \\ z = - t \end{matrix}, ∆_{2} : \{\begin{matrix} x = 4 + t \\ y = 3 - 2 t \\ z = 1 - t \end{matrix}$ .Gọi (S) là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng Δ₁ và Δ₂. Bán kính mặt cầu (S).

$A . \frac{\sqrt{10}}{2}$

$B . \frac{\sqrt{11}}{2}$

C. 3/2

D. $\sqrt{2}$

Xem lời giải »

Câu 16:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 = 0. Hình chiếu vuông góc của điểm M lên mặt phẳng (P) là:

A. H (1; 2; 2)

B. H (2; 5; 3)

C. H (6; 7; 8)

D. H (2; -3; -1)

Xem lời giải »

Câu 17:

Cho khối cầu tâm O bán kính 6 cm. Mặt phẳng (P) cách O một khoảng x cắt khối cầu theo một hình tròn (C). Một khối nón có đỉnh thuộc mặt cầu, đáy là hình tròn (C). Biết khối nón có thể tích lớn nhất, giá trị của x bằng:

A. 2 cm.

B. 3 cm.

C. 4 cm.

D. 0 cm.

Xem lời giải »

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 2}{2} = \frac{y}{- 1} = \frac{z}{4}$ và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 2$ . Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng?

A. 2 $\sqrt{2}$

$B . \frac{4 \sqrt{3}}{3}$

$C . \frac{2 \sqrt{3}}{3}$

D. 4

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x + y + 6z -1 = 0 và hai điểm A (1; -1; 0), B (-1; 0; 1). Hình chiếu vuông góc của đoạn thẳng AB trên mặt phẳng (P) có độ dài bao nhiêu?

$A . \sqrt{\frac{255}{61}}$

$B . \sqrt{\frac{237}{41}}$

$C . \sqrt{\frac{137}{41}}$

$D . \sqrt{\frac{155}{61}}$

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M (1; 3; -2), cắt các tia Ox, Oy, OZ lần lượt tại A, B, C sao cho $\frac{O A}{1} = \frac{O B}{2} = \frac{O C}{4}$

$A . 2 x - y - z - 1 = 0$

$B . x + 2 y + 4 z + 1 = 0$

$C . 4 x + 2 y + z + 1 = 0$

$D . 4 x + 2 y + z - 8 = 0$

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (-1; -2; 0), B (0; -4; 0), C (0; 0; -3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?

$A . (P) : 2 x - y + 3 z = 0$

$B . (P) : 6 x - 3 y + 5 z = 0$

$C . (P) : 2 x - y - 3 z = 0$

$D . (P) : - 6 x + 3 y + 4 z = 0$

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z -5 = 0, A (-3; 0; 1), B (1; -1; 3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.

$A . \frac{x + 3}{1} = \frac{y}{- 1} = \frac{z - 1}{2}$

$B . \frac{x + 3}{3} = \frac{y}{- 2} = \frac{z - 1}{2}$

$C . \frac{x - 1}{1} = \frac{y}{- 2} = \frac{z - 1}{2}$

$D . \frac{x + 3}{2} = \frac{y}{- 6} = \frac{z - 1}{- 7}$

Xem lời giải »

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng

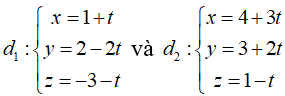
Trên đường thẳng d₁ lấy hai điểm A, B thỏa mãn AB = 3 . Trên đường thẳng d₂lấy hai điểm C, D thỏa mãn CD = 4. Tính thể tích của tứ diện ABCD.

A. V = 7

B. V = 2√21

C. $V = \frac{4 \sqrt{21}}{3}$

D. $V = \frac{5 \sqrt{21}}{6}$

Xem lời giải »

Câu 24:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\hat{A B C} = 60^{o}$ . Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn BC sao cho BC = 4 BH. Biết SA tạo với đáy một góc 60⁰. Lấy D thuộc tia SB sao cho 2SD = 3SB. Góc giữa hai đường thẳng AD và SC bằng:

A. 60⁰

B. 45⁰

C. 90⁰

D. 30⁰

Xem lời giải »

Câu 25:

Trong không gian Oxyz, cho điểm M (1; 1; 2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi $\vec{n} = (1; a; b)$ là một véc tơ pháp tuyến của (P). Tính S = a³- 2b

A. S = 0

B. S = - 3

C. S = 6

D. S = -15/8

Xem lời giải »

Câu 1:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{1}$ và mặt phẳng (α): x + y -z – 2 = 0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?

$A . ∆_{2} : \frac{x - 2}{1} = \frac{y - 4}{- 2} = \frac{z - 4}{3}$

$B . ∆_{4} : \frac{x - 1}{3} = \frac{y - 1}{- 2} = \frac{z}{1}$

$C . ∆_{3} : \frac{x - 5}{3} = \frac{y - 2}{- 2} = \frac{z - 5}{1}$

$D . ∆_{1} : \frac{x + 2}{- 3} = \frac{y + 4}{2} = \frac{z + 4}{- 1}$

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho mặt phẳng (α): 2x + y -2z – 2 = 0, đường thẳng $d : \frac{x + 1}{1} = \frac{y + 2}{2} = \frac{z + 3}{2}$ và điểm $A (\frac{1}{2}; 1; 1)$ . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng Δ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng.

A. 7/2

B. √21/2

C. 7/3

D. 3/2

Xem lời giải »

Câu 3:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD (tham khảo hình vẽ bên).

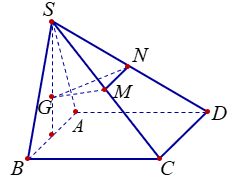
Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD)

$A . \frac{2 \sqrt{39}}{39}$

$B . \frac{\sqrt{3}}{6}$

$C . \frac{2 \sqrt{39}}{13}$

$D . \frac{\sqrt{13}}{13}$

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho mặt phẳng $(α)$ x – z – 3 = 0 và điểm M (1; 1; 1). Gọi A là điểm thuộc tia Oz. Gọi B là hình chiếu của A lên (α). Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng:

A. $6 \sqrt{3}$

$B . \frac{3 \sqrt{3}}{12}$

$C . \frac{3 \sqrt{123}}{2}$

D. $3 \sqrt{3}$

Xem lời giải »

Câu 5:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho MA² + MB² đạt giá trị nhỏ nhất.

A. M (0; 0; 49)

B. M (0; 0; 67)

C. M (0; 0 ;3)

D. M (0; 0; 0)

Xem lời giải »

Câu 6:

Trong không gian tọa độ Oxyz, cho điểm M (2; 0; 0), N (1; 1; 1). Mặt phẳng (P) thay đổi qua M, N cắt các trục Ox, Oy lần lượt tại B (0; b; 0), C (0; 0; c) (b, c > 0). Hệ thức nào dưới đây là đúng?

A. bc = 2 (b+c)

B. $b c = \frac{1}{b} + \frac{1}{c}$

C. bc = b + c

D. bc = b - c

Xem lời giải »

Câu 7:

Trong không gian tọa độ Oxyz, cho điểm A (0; 0; -2) và đường thẳng $∆ : \frac{x + 2}{2} = \frac{y - 2}{3} = \frac{z + 3}{2}$ . Phương trình mặt cầu tâm A, cắt Δ tại hai điểm B và C sao cho BC = 8 là:

$A . (S) : x^{2} + y^{2} + {(z + 2)}^{2} = 16$

$B . (S) : x^{2} + y^{2} + {(z + 2)}^{2} = 25$

$C . (S) : {(x + 2)}^{2} + {(y + 3)}^{2} + {(z + 1)}^{2} = 16$

$D . (S) : {(x + 2)}^{2} + y^{2} + z^{2} = 25$

Xem lời giải »

Câu 8:

Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1; 0; -1), B (2; 3; -1), C (-2; 1; 1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:

$A . \frac{x}{3} = \frac{y - 2}{- 1} = \frac{z}{5}$

$B . \frac{x}{3} = \frac{y - 2}{1} = \frac{z}{5}$

$C . \frac{x - 1}{1} = \frac{y}{- 2} = \frac{z + 1}{2}$

$D . \frac{x - 3}{3} = \frac{y - 2}{- 1} = \frac{z - 5}{5}$

Xem lời giải »

Câu 9:

Trong không gian tọa độ Oxyz, cho các điểm A (1; 2; 3), B (2; 1; 0), C (4; 3; -2), D (3; 4; 1), E (1; 1; -1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?

A. 1

B. 4

C. 5

D. Không tồn tại.

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng $∆ : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z}{- 1}$ . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:

$A . d : \{\begin{matrix} x = 2 + t \\ y = 1 - 4 t \\ z = - 2 t \end{matrix}$

$B . d : \{\begin{matrix} x = 2 - t \\ y = 1 + t \\ z = t \end{matrix}$

$C . d : \{\begin{matrix} x = 1 + t \\ y = - 1 - 4 t \\ z = 2 t \end{matrix}$

$D . d : \{\begin{matrix} x = 2 + 2 t \\ y = 1 + t \\ z = - t \end{matrix}$

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 16$ và điểm A (1; 2; 3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.

A. 10π

B. 38π

C. 33π

D. 36π

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz cho điểm A (2; 1; 3) và mặt phẳng (P): x + my + (2m + 1)z – m – 2 = 0, m là tham số. Gọi H (a; b; c) là hình chiếu vuông góc của điểm A trên (P). Tính a + b khi khoảng cách từ điểm A đến (P) lớn nhất?

A. a + b = -1/2

B. a + b = 2

C. a + b = 0

D. a + b = 3/2

Xem lời giải »

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a $\sqrt{3}$ ,SA = a và SA vuông góc với đáy ABCD. Tính sinα, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)

$A . \sin α = \frac{\sqrt{7}}{8}$

$B . \sin α = \frac{\sqrt{3}}{2}$

$C . \sin α = \frac{\sqrt{2}}{4}$

$D . \sin α = \frac{\sqrt{3}}{5}$

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3) và mặt phẳng (P): 2x + y - 4z + 1 = 0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.

$A . \{\begin{matrix} x = 1 + 5 t \\ y = 2 - 6 t \\ z = 3 + t \end{matrix}$

$B . \{\begin{matrix} x = t \\ y = 2 t \\ z = 2 + t \end{matrix}$

$C . \{\begin{matrix} x = 1 + 3 t \\ y = 2 + 2 t \\ z = 3 + t \end{matrix}$

$D . \{\begin{matrix} x = 1 - t \\ y = 2 + 6 t \\ z = 3 + t \end{matrix}$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.

A. 36π

B. $36 \sqrt{2} π$

C. $18 \sqrt{2} π$

D. 18π

Xem lời giải »

Câu 16:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2; -3; 2), B (3; 5; 4). Tìm toạ độ điểm M trên trục Oz sao cho $M A^{2} + M B^{2}$ đạt giá trị nhỏ nhất.

A. M (0; 0; 49).

B. M (0; 0; 67)

C. M (0; 0 ;3)

D. M (0; 0; 0)

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 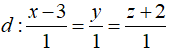và điểm M(2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?

A. 2.

B. 1.

C. 0.

D. Vô số.

Xem lời giải »

Câu 18:

Trong không gian tọa độ Oxyz, cho điểm A(1;-2; 3). Gọi (S) là mặt cầu chứa A có tâm I thuộc tia Ox và bán kính bằng 7. Phương trình mặt cầu (S) là:

$A . {(x + 5)}^{2} + y^{2} + z^{2} = 49$

$B . {(x + 7)}^{2} + y^{2} + z^{2} = 49$

$C . {(x - 3)}^{2} + y^{2} + z^{2} = 49$

$D . {(x - 7)}^{2} + y^{2} + z^{2} = 49$

Xem lời giải »

Câu 19:

Trong không gian Oxyz, cho bốn đường thẳng:

$d_{1} : \frac{x - 3}{1} = \frac{y + 1}{- 2} = \frac{z + 1}{1}, d_{2} : \frac{x}{1} = \frac{y}{- 2} = \frac{z - 1}{1}, d_{3} : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 1}{1}, d_{4} : \frac{x}{1} = \frac{y - 1}{- 1} = \frac{z - 1}{1}$

Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:

A. 0.

B. 2.

C. Vô số.

D. 1.

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-y+z-10 = 0 và đường thẳng . Đường thẳng Δ cắt (P) và d lần lượt tại M và N sao cho A(1;3;2) là trung điểm MN. Tính độ dài đoạn MN.

$A . M N = 4 \sqrt{33}$

$B . M N = 2 \sqrt{26, 5}$

$C . M N = 4 \sqrt{16, 5}$

$D . M N = 2 \sqrt{33}$

Xem lời giải »

Câu 21:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-4), B(1;-3;1), C(2;2;3). Tính đường kính d của mặt cầu (S) đi qua ba điểm trên và có tâm nằm trên mặt phẳng (Oxy).

A. d = $2 \sqrt{13}$

B. d = $2 \sqrt{41}$

C. d = $2 \sqrt{26}$

D. d = $2 \sqrt{11}$

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).

A. 3x + 2y + z + 14 = 0

B. 2x + y + 3z + 9 = 0

C. 3x + 2y + z - 14 = 0

D. 2x + y + z - 9 = 0.

Xem lời giải »

Câu 23:

Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABC) bằng 60°. Khoảng cách giữa hai đường thẳng BC và DM là:

$A . a \sqrt{\frac{15}{62}}$

$B . a \sqrt{\frac{30}{31}}$

$C . a \sqrt{\frac{15}{68}}$

$D . a \sqrt{\frac{15}{17}}$

Xem lời giải »

Câu 24:

Trong không gian với hệ tọa độ Oxyz, cho ΔABC biết A(2;0;0), B(0;2;0), C(1;1;3). Gọi H(x₀;y₀;z₀) là chân đường cao hạ từ đỉnh A xuống BC. Khi đó x₀+ y₀+ z₀ bằng:

A. 38/9

B. 34/11

C. 30/11

D. 11/34

Xem lời giải »

Câu 25:

Cho tứ diện ABCD có các cạnh AB, AC, AD vuông góc với nhau từng đôi một và AB = 3a , AC = 6a, AD = 4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, DB. Tính thể tích khối đa diện AMNP.

A. $3 a^{3}$

B. $12 a^{3}$

C. $a^{3}$

D. $2 a^{3}$

Xem lời giải »

Câu 1:

Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) có tâm nằm trên đường thẳng $d : \frac{x}{1} = \frac{y - 1}{1} = \frac{z - 2}{1}$ và tiếp xúc với hai mặt phẳng (P): 2x - z - 4 = 0, (Q): x – 2y – 2 = 0

$A . (S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 5$

$B . (S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = \sqrt{5}$

$C . (S) : {(x + 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2} = 5$

$D . (S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 3$

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (S): x + 2y – 2z + 2018 = 0 và (Q): x + my + (m -1)z + 2017 = 0. Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm H nào dưới đây nằm trong mặt phẳng (Q)?

A. H (-2017; 1; 1)

B. H (2017; -1; 1)

C. H (2017; 0; 0)

D. H (0; -2017; 0)

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau

$d_{1} : \{\begin{matrix} x = 4 - 2 t \\ y = t \\ z = 3 \end{matrix}, d_{2} : \{\begin{matrix} x = 1 \\ y = t' \\ z = - t' \end{matrix}$

Phương trình mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng trên là:

Xem lời giải »

Câu 4:

Trong không gian với tọa độ Oxyz, cho hai điểm A (1;1;2), B (-1; 3; -9). Tìm tọa độ điểm M thuộc Oy sao cho $△ A B M$ vuông tại M.

Xem lời giải »

Câu 5:

Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính bóng bàn. Gọi S₁ là tổng diện tích của ba quả bóng bàn, S₂ là diện tích xung quanh của hình trụ. Tỉ số S₁/S₂bằng:

A. 1.

B. 1, 2.

C. 2.

D. 1, 5.

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $∆ : \frac{x + 1}{2} = \frac{y}{3} = \frac{z + 1}{- 1}$ và hai điểm A(1; 2; -1); B (3; -1; -5). Gọi d là đường thẳng đi qua điểm A và cắt đường thẳng Δ sao cho khoảng cách từ điểm B đến đường thẳng d là lớn nhất. Phương trình đường thẳng d là:

$A . \frac{x - 3}{2} = \frac{y}{2} = \frac{z + 5}{- 1}$

$B . \frac{x}{- 1} = \frac{y + 2}{3} = \frac{z}{4}$

$C . \frac{x + 2}{3} = \frac{y}{1} = \frac{z - 1}{- 1}$

D. Tất cả sai

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:

A. 245/108

B. 9/4

C. 64/27

D. 75/32

Xem lời giải »

Câu 8:

Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S) có phương trình ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 1$ . Một phương trình mặt phẳng (Q) chứa trục hoành và tiếp xúc với mặt cầu (S) là:

A. 4y + 3z = 0

B. 4y + 3z + 1 = 0

C. 4y - 3z + 1 = 0

D. 4y - 3z = 0

Xem lời giải »

Câu 9:

Trong không gian Oxyz, cho tám điểm A (-2;-2;0), B (3;-2;0), C (3;3;0), D (-2;3;0), M(-2;-2;5), N(3;3;5), P(3;-2;5), Q(-2;3;5) . Hình đa diện tạo bởi tám điểm đã cho có bao nhiêu mặt đối xứng?

A. 3

B. 9

C. 8

D. 6

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng $d : \frac{x - 2}{2} = \frac{y - 3}{3} = \frac{z + 4}{- 5}$ và $d' : \frac{x + 1}{3} = \frac{y - 4}{- 2} = \frac{z - 4}{- 1}$

Xem lời giải »

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; -2; -1), B (-2,-4,3), C (1;3;-1) và mặt phẳng (P): x + y -2z – 3 = 0. Tìm điểm M ∈ (P) sao cho $|\vec{M A} + \vec{M B} + 2 \vec{M C}|$ đạt giá trị nhỏ nhất.

$A . M (\frac{1}{2}; \frac{1}{2}; - 1)$

$B . M (- \frac{1}{2}; - \frac{1}{2}; 1)$

$C . M (2; 2; - 4)$

$D . M (- 2; - 2; 4)$

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + z – 4 = 0 và đường thẳng $d : \frac{x + 1}{2} = \frac{y}{1} = \frac{z + 2}{3}$ . Viết phương trình đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.

Xem lời giải »

Câu 13:

Trong không gian với hệ tọa độ Oxyz, xét đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx. Tính khoảng cách nhỏ nhất giữa điểm B (0; 4; 0) tới điểm C trong đó C là điểm cách đều đường thẳng Δ và trục Ox.

A. 1/2

B. $3 \sqrt{2}$

C. $\sqrt{6}$

D. $\sqrt{65} / 2$

Xem lời giải »

Câu 14:

Trong không gian với hệ trục Oxyz, cho hai điểm M (0;-1;2), N (-1; 1; 3). Một mặt phẳng (P) đi qua M, N sao cho khoảng cách từ điểm K (0;0;2) đến mặt phẳng (P) đạt giá trị nhỏ nhất. Tìm tọa độ véctơ pháp tuyến của mặt phẳng (P).

$A . \vec{n} = (1; - 1; 1)$

$B . \vec{n} = (1; 1; - 1)$

$C . \vec{n} = (2; - 1; 1)$

$D . \vec{n} = (2; 1; - 1)$

Xem lời giải »

Câu 15:

Trong không gian Oxyz cho mặt cầu (S): (x - 3)² + (y - 1)² + z² = 4 và đường thẳng $d : \{\begin{matrix} x = 1 + 2 t \\ y = - 1 + t, t \in ℝ \\ z = - t \end{matrix}$ . Mặt phẳng chứa d và cắt (S) theo một đường tròn có bán kính nhỏ nhất có phương trình là:

A. 3x-2y-4z-8=0

B. y+z+1=0

C. x-2y-3=0

D. x+3y+5z+2=0

Xem lời giải »

Câu 16:

Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng $∆ : \frac{x - 1}{2} = \frac{y}{1} = \frac{z - 3}{- 1}, ∆' : \frac{x}{1} = \frac{y + 1}{- 2} = \frac{z - 2}{1}$ .

Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:

Xem lời giải »

Câu 17:

Trong không gian Oxyz, cho hai đường thẳng $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 2}{2}$ và $d' : \frac{x + 1}{1} = \frac{y}{2} = \frac{z - 1}{1}$ . Phương trình mặt phẳng chứa đường thẳng d và tạo với đường thẳng d' một góc lớn nhất là:

A. x - z + 1 = 0.

B. x - 4y + z - 7 = 0

C. 3x - 2y - 2z - 1 = 0.

D. -x + 4y - z - 7 = 0.

Xem lời giải »

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x - y + z - 4 = 0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)² =16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:

$A . M (- \frac{1}{2}; 0; 0)$

$B . M (- \frac{1}{3}; 0; 0)$

$C . M (1; 0; 0)$

$D . M (\frac{1}{3}; 0; 0)$

Xem lời giải »

Câu 19:

Trong không gian Oxyz, cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến $∆$ kẻ từ B là $\frac{x - 3}{- 1} = \frac{y - 3}{2} = \frac{z - 2}{- 1}$ , phương trình đường phân giác trong $d$ của góc C là $\frac{x - 2}{2} = \frac{y - 4}{- 1} = \frac{z - 2}{- 1}$ . Đường thẳng BC có một vectơ chỉ phương là:

$A . \vec{u} = (2; 1; - 1)$

$B . \vec{u} = (1; 1; 0)$

$C . \vec{u} = (1; - 1; 0)$

$D . \vec{u} = (1; 2; 1)$

Xem lời giải »

Câu 20:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông, tam giác SAB cân tại S. Góc giữa mặt bên (SAB) và mặt đáy bằng $60 °$ , góc giữa SA và mặt phẳng đáy bằng 45⁰. Biết thể tích khối chóp S. ABCD bằng $\frac{8 a^{3} \sqrt{3}}{3}$ . Chiều cao của hình chóp S. ABCD bằng:

A. $a \sqrt{3}$

B. $a \sqrt{6}$

$C . \frac{a \sqrt{3}}{3}$

$D . \frac{a \sqrt{2}}{3}$

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;2;3), B (0;4;5). Gọi M là điểm sao cho MA=2MB. Khoảng cách từ điểm M đến mặt phẳng (P): 2x - 2y - z + 6 = 0 đạt giá trị nhỏ nhất xấp xỉ là bao nhiêu?

A.1,12

B.1,17

C.1,21

D.1,22

Xem lời giải »

Câu 22:

Cho tứ diện ABCD có M, N, P lần lượt thuộc các cạnh AB, BC, CD sao cho MA=MB, NB=2NC, PC=2PD. Mặt phẳng (MNP) chia tứ diện thành hai phần. Gọi T là tỉ số thể tích của phần nhỏ chia phần lớn. Giá trị của T bằng?

A. 13/25

B. 25/43

C. 19/26

D. 26/45

Xem lời giải »

Câu 23:

Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết điểm A (1; 2; 3), đường trung tuyến BM và đường cao CH có phương trình tương ứng là $\{\begin{matrix} x = 5 t \\ y = 0 \\ z = 1 + 4 t \end{matrix}$ và $\frac{x - 4}{16} = \frac{y + 2}{- 13} = \frac{z - 3}{5}$ . Viết phương trình đường phân giác góc A.

$A . \frac{x - 1}{7} = \frac{y - 2}{- 1} = \frac{z - 3}{10}$

$B . \frac{x - 1}{4} = \frac{y - 2}{13} = \frac{z - 3}{5}$

$C . \frac{x - 1}{2} = \frac{y - 2}{- 3} = \frac{z - 3}{- 1}$

$D . \frac{x - 1}{2} = \frac{y - 2}{- 11} = \frac{z - 3}{- 5}$

Xem lời giải »

Câu 24:

Trong không gian Oxyz cho điểm M (2;1;5). Mặt phẳng (P) đi qua điểm M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho M là trực tâm của tam giác ABC. Tính khoảng cách từ điểm I (1;2;3) đến mặt phẳng (P)

$A . \frac{17 \sqrt{30}}{30}$

$B . \frac{13 \sqrt{30}}{30}$

$C . \frac{19 \sqrt{30}}{30}$

$D . \frac{11 \sqrt{30}}{30}$

Xem lời giải »

Câu 25:

Trong không gian (Oxy) cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là $\frac{x - 3}{- 1} = \frac{y - 3}{2} = \frac{z - 2}{- 1}$ , phương trình đường phân giác trong góc C là $\frac{x - 2}{2} = \frac{y - 4}{- 1} = \frac{z - 2}{- 1}$ . Biết rằng $\vec{u} = (m; n; - 1)$ là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị biểu thức T=m²+n².

A. T=1

B. T=5

C. T=2

D. T=10

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và đường thẳng $∆ : \frac{x - 6}{- 3} = \frac{y - 2}{2} = \frac{z - 2}{2}$ . Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:

A.x - 2y + 2z - 1 = 0.

B.2x + 2y + z - 18 = 0.

C.2x - y - 2z - 10 = 0.

D.2x + y + 2z - 19 = 0.

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto $\vec{u} = (a, b, c)$ làm vectơ chỉ phương và song song với mặt phẳng (P): 2x + y + z = 0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:

A. 15

B. 13

C. 16

D. 14

Xem lời giải »

Câu 3:

Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S).

A.3.

B. 0

C. 1

D. 2

Xem lời giải »

Câu 4:

Trong không gian Oxyz cho A (1;2;-1), B (3;1;-2), C (2;3;-3) và mặt phẳng (P): x-2y+2z-3=0. M (a;b;c) là điểm thuộc mặt phẳng (P) sao cho biểu thức MA²+MB²+MC² có giá trị nhỏ nhất. Xác định a+b+c.

A. -3

B. -2

C. 2

D. 3

Xem lời giải »

Câu 5:

Trong không gian tọa độ Oxyz cho A (1; 1; -1), B (2; 3; 1), C (5; 5; 1). Đường phân giác trong góc A của tam giác ABC cắt mặt phẳng (Oxy) tại M (a; b; 0). Tính 3b-a.

A. 6.

B. 5.

C. 3.

D. 0.

Xem lời giải »

Câu 6:

Trong không gian Oxyz cho mặt phẳng (P): 5x + my + 4z + n = 0 đi qua giao tuyến của hai mặt phẳng (α): 3x - 7y + z - 3 = 0 và (β): x - 9y - 2z + 5 = 0. Tính m + n.

A. 6.

B. -16.

C. -3.

D. -4.

Xem lời giải »

Câu 7:

Cho hình lập phương ABCD. A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và DCC'D'. Mặt phẳng (A'MN) chia khối lập phương trình hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỷ số V₂/V₁

A. 5/2

B. 5/3

C. 3/2

D. 2

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho mặt cầu (S): (x -1)²+ (y + 2)² + (z - 3)² = 27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax + by - z + c = 0, khi đó a - b + c bằng:

A. -4.

B. 8.

C. 0.

D. 2.

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng

$d_{1} : \frac{x - 1}{2} = \frac{y - 1}{- 1} = \frac{z + 1}{1}, d_{2} : \frac{x + 2}{3} = \frac{y + 1}{1} = \frac{z - 2}{2}$ . Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:

A. √38

B. 2√10

C. 8

D. 12

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I (1;0;-1) và cắt mặt phẳng (P): 2x+y-2z-16=0 theo giao tuyến là một đường tròn có bán kính bằng 3. Phương trình của mặt cầu (S) là:

A. (x-1)²+y²+ (z+1)²=25.

B.(x+1)²+y²+ (z-1)²=25

C. (x-1)²+y²+ (z+1)²=9.

D.(x+1)²+y²+ (z-1)²=9.

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 4x+y+2z+1=0 và điểm M(4;2;1). Khi đó điểm đối xứng với M qua mặt phẳng (P) là:

A. M'(-4;0;-3).

B. M'(-4;-4;-1).

C. M'(4;2;1).

D. M'(-2;0;5).

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là:

$A . \{\begin{cases} x = \frac{8}{3} + 26 t y = \frac{5}{3} + 22 t \\ z = \frac{4}{3} + 27 t \end{cases}$

$B . \{\begin{cases} x = 4 + 26 t y = 2 + 22 t \\ z = \frac{9}{4} + 27 t \end{cases}$

$C . \{\begin{cases} x = \frac{11}{6} y = \frac{1}{6} + 22 t \\ z = 27 t \end{cases}$

$D . \{\begin{cases} x = 4 + 26 t y = 2 + 38 t \\ z = \frac{9}{4} + 27 t \end{cases}$

Xem lời giải »

Câu 13:

Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng $d : \frac{x - 3}{1} = \frac{y - 3}{3} = \frac{z}{2}$ , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho mặt phẳng (P):x+y+z-1=0 và hai điểm A (1;-3;0), B (5;-1;-2). Điểm M (a;b;c) nằm trên (P) và |MA – MB| lớn nhất. Giá trị abc bằng:

A. 1

B. 12

C. 24.

D. -24.

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: $\frac{x}{10} = \frac{y + 2}{8} = \frac{z - 1}{1}$ và mặt cầu (S): x²+y²+z²+2x-6y+4z-15=0. Mặt phẳng chứa d, tiếp xúc với (S) và cắt trục Oz tại điểm có cao độ lớn hơn 3 có phương trình là:

A. 2x-3y+4z-10=0.

B. 2x-3y+4z-12=0.

C. 3x-4y+2z-12=0.

D. 3x-4y+2z-10=0.

Xem lời giải »

Câu 16:

Cho hình hộp chữ nhật ABCD. A'B'C'D' có đáy ABCD là hình vuông cạnh a, AA'=b. Gọi M là trung điểm của cạnh CC'. Tính theo a và b thể tích V của khối tứ diện BDA'M

Xem lời giải »

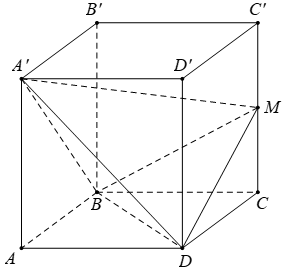
Câu 17:

Trong không gian Oxyz, cho hai đường thẳng d₁ và d₂ lần lượt có phương trình là $\frac{x}{1} = \frac{y + 1}{2} = \frac{z}{1} v à \frac{x}{1} = \frac{y - 1}{- 2} = \frac{z - 1}{3}$ .Đường thẳng d cắt cả hai đường thẳng d₁, d₂ và song song với đường thẳng $∆ : \frac{x - 4}{1} = \frac{y - 7}{4} = \frac{z - 3}{- 2}$ có phương trình là:

Xem lời giải »

Câu 18:

Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng $d : \frac{x - 3}{1} = \frac{y - 3}{3} = \frac{z}{2}$ , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).

Xem lời giải »

Câu 19:

Trong không gian Oxyz, cho hai đường thẳng chéo nhau $d : \frac{x - 3}{- 4} = \frac{y + 2}{1} = \frac{z + 1}{1}$ và $d^{'} : \frac{x}{- 6} = \frac{y - 1}{1} = \frac{z - 2}{2}$ . Phương trình nào dưới đây là phương trình đường thẳng vuông góc chung của d và d'?

Xem lời giải »

Câu 20:

Trong không gian Oxyz, cho tam giác ABC với A (3;0;0), B (0;6;0), C (0;0;6). Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC).

Xem lời giải »

Câu 21:

Trong không gian Oxyz, cho mặt cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P): ax + by + cz - 2 = 0 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M = 2a + b - c.

A. M = 2.

B. M = 3.

C. M = 1.

D. M = 4.

Xem lời giải »

Câu 22:

Trong không gian Oxyz cho mặt cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M (a; b; c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất. Khi đó:

A. a + b + c = 8.

B. a + b + c = 5.

C. a + b + c = 6.

D. a + b + c = 7.

Xem lời giải »

Câu 23:

Trong không gian Oxyz, cho hai điểm M (-2;-2;1), A (1;2;-3) và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ .Tìm véctơ chỉ phương $\vec{u}$ của đường thẳng Δ đi qua M, vuông góc với đường thẳng d, đồng thời cách điểm A một khoảng lớn nhất.

Xem lời giải »

Câu 24:

Trong không gian Oxyz cho điểm M (1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x'Ox, y'Oy, z'Oz lần lượt tại ba điểm phân biệt A, B, C sao cho OA = OB = OC ≠ 0.

A. 1.

B. 2.

C. 4

D. 3.

Xem lời giải »

Câu 25:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 2}{3} = \frac{y + 1}{1} = \frac{z + 5}{- 1}$ và mặt phẳng (P):2x-3y+z-6=0. Phương trình nào dưới đây là phương trình của đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với (d)?

Xem lời giải »

Câu 1:

Trong không gian Oxyz, mặt cầu (S) tâm I (2; 5; 3) cắt đường thẳng tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + $2 \sqrt{7}$ . Phương trình nào sau đây là phương trình của mặt cầu (S)?

A. (x - 2)² + (y - 5)² + (z - 3)² = 100.

B. (x - 2)² + (y - 5)² + (z - 2)² = 7.

C. (x - 2)² + (y - 5)² + (z - 3)² = 25.

D. (x - 2)² + (y - 5)² + (z - 3)² = 28.

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z - 5 = 0, A (-3;0;1), B (1;-1;3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} \{\begin{cases} x = 1 + t y = 2 - 2 t \\ z = - 3 - t \end{cases}$ và $d_{2} \{\begin{cases} x = 4 + 3 t y = 3 + 2 t \\ z = 1 - t \end{cases}$ . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mãn AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.

A. V=7

B. V=2 $\sqrt{21}$

C.V= $\frac{4 \sqrt{21}}{3}$

D.V= $\frac{5 \sqrt{21}}{6}$

Xem lời giải »

Câu 4:

Cho hình chóp S. ABC có đáy ABC là tam giác vuông tại A, góc ABC = $60^{o}$ , BC = 2a. Gọi D là điểm thỏa mãn $3 \vec{S B} = 2 \vec{S D}$ . Hình chiếu của S trên mặt phẳng (ABC) là điểm H thuộc đoạn BC sao cho BC = 4BH. Biết SA tạo với đáy một góc 60⁰. Góc giữa hai đường thẳng AD và SC bằng:

A. 60⁰.

B. 45⁰.

C. 90⁰.

D. 30⁰.

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho điểm M (1;1;2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi là một véc tơ pháp tuyến của (P). Tính S = a³ - 2b.

A. S = 0.

B. S = -3.

C. S = 6.

D. S = -15/8

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{1} = \frac{y - 2}{2} = \frac{z - 3}{1}$ và mặt phẳng (α): x+y-z-2=0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng $d : \frac{x + 1}{1} = \frac{y + 2}{2} = \frac{z + 3}{2}$ và điểm $A (\frac{1}{2}; 1; 1)$ . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:

A. 7/2

B. $\sqrt{21} / 2$

C. 7/3

D. 3/2

Xem lời giải »

Câu 8:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD. Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD).

Xem lời giải »

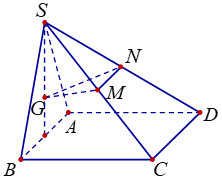
Câu 9:

#THPTTrong không gian Oxyz cho mặt phẳng (α): x – z – 3 = 0 và điểm M (1;1;1). Gọi A là điểm thuộc tia Oz. Gọi B là hình chiếu của A lên (α). Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng:

A $\frac{3 \sqrt{2}}{2}$

B $\frac{3 \sqrt{3}}{2}$

C $\frac{\sqrt{3}}{2}$

D $\sqrt{3}$

Xem lời giải »

Câu 10:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất.

A. M (0;0;49)

B. M (0;0;67)

C. M (0;0;3)

D. M (0;0;0)

Xem lời giải »

Câu 11:

Trong không gian tọa độ Oxyz, cho điểm M (2;0;0), N (1;1;1). Mặt phẳng (P) thay đổi qua M, N cắt các trục Ox, Oy lần lượt tại B (0;b;0), C (0;0;c) (b > 0, c > 0). Hệ thức nào dưới đây là đúng?

A. bc=2 (b+c).

B. $bc = \frac{1}{b} + \frac{1}{c}$

C. b+c=bc.

D. bc=b-c.

Xem lời giải »

Câu 12:

Trong không gian tọa độ Oxyz, cho điểm A (0;0;-2) và đường thẳng $∆ : \frac{x + 2}{2} = \frac{y - 2}{3} = \frac{z + 3}{2}$ . Phương trình mặt cầu tâm A, cắt Δ tại hai điểm B và C sao cho BC = 8 là:

A. (S):x²+y²+ (z+2)²=16.

B. (S):x²+y²+ (z+2)²=25.

C. (S): (x+2)²+ (y-3)²+ (z+1)²=16.

D. (S): (x+2)²+y²+z²=25.

Xem lời giải »

Câu 13:

Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:

Xem lời giải »

Câu 14:

Trong không gian tọa độ Oxyz, cho các điểm A (1;2;3), B (2;1;0), C (4;3;-2), D (3;4;1), E (1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?

A. 1

B. 4.

C. 5

D. Không tồn tại.

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;0) và đường thẳng $∆ : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z}{- 1}$ .Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:

Xem lời giải »

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)²= 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua I là tâm của mặt cầu (S) và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.

A. 10π.

B. 38 π

C. 33 π

D. 36 π

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oyz cho điểm A (2;1;3) và mặt phẳng (P): x+my+ (2m+1)z-m-2=0, m là tham số. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất?

A. $a + b = - \frac{1}{2}$

B. a+b=2

C. a+b=0

D. $a + b = \frac{3}{2}$

Xem lời giải »

Câu 18:

#SGD Bắc Giang – năm 2017 – 2018~Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, AB=a, BC = a $\sqrt{3}$ , SA=a và SA vuông góc với đáy ABCD. Tính sin α, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;3) và mặt phẳng (P): 2x+y-4z+1=0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0;1;1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.

A. 36π

B. 36 $\sqrt{2}$ π

C. 18 $\sqrt{2}$ π

D. 18 π

Xem lời giải »

Câu 21:

Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz sao cho MA²+MB² đạt giá trị nhỏ nhất.

A. M (0;0;49)

B. M (0;0;67)

C. M (0;0;3)

D. M (0;0;0).

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 3}{1} = \frac{y}{1} = \frac{z + 2}{1}$ và điểm M (2; -1; 0). Gọi (S) là mặt cầu có tâm I thuộc đường thẳng d và tiếp xúc với mp (Oxy) tại điểm M. Hỏi có bao nhiêu mặt cầu thỏa mãn?

A. 2.

B. 1

C. 0.

D. Vô số.

Xem lời giải »

Câu 23:

Trong không gian tọa độ Oxyz, cho điểm A (1;-2;3). Gọi (S) là mặt cầu chứa A có tâm I thuộc tia Ox và bán kính bằng 7. Phương trình mặt cầu (S) là:

A. (x+5)²+y²+z²=49.

B. (x+7)²+y²+z²=49.

C. (x-3)²+y²+z²=49.

D. (x-7)²+y²+z²=49.

Xem lời giải »

Câu 24:

Trong không gian Oxyz, cho bốn đường thẳng $d_{1} : \frac{x - 3}{1} = \frac{y + 1}{- 2} = \frac{z + 1}{1}$ ; $d_{2} : \frac{x}{1} = \frac{y}{- 2} = \frac{z - 1}{1}$ ; $d_{3} : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 1}{1}$ ; $d_{4} : \frac{x}{1} = \frac{y - 1}{- 1} = \frac{z - 1}{1}$ . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:

A. 0.

B. 2.

C. Vô số.

D. 1.

Xem lời giải »

Câu 25:

Trong không gian Oxy, cho điểm M (-1;1;2) và hai đường thẳng $d : \frac{x - 2}{3} = \frac{y + 3}{2} = \frac{z - 1}{1}$ , $d^{'} : \frac{x + 1}{1} = \frac{y}{3} = \frac{z}{- 2}$ . Phương trình nào dưới đây là phương trình đường thẳng đi qua điểm M, cắt d và vuông góc với d' ?

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;1). Viết phương trình mặt phẳng (P) đi qua M và cắt ba tia Ox, Oy, Oz lần lượt tại các điểm A, B, C khác gốc O sao cho thể tích khối tứ diện OABC nhỏ nhất.

A. 2x-y+2z-3=0.

B. 4x-y-z-6=0

C. 2x+y+2z-6=0

D. x+2y+2z-6=0.

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho hai điểm M (2;2;1), $N (\frac{- 8}{3}; \frac{4}{3}; \frac{8}{3})$ . Viết phương trình mặt cầu có tâm là tâm của đường tròn nội tiếp tam giác OMN và tiếp xúc với mặt phẳng (Oxz).

A. x²+ (y+1)²+ (z+1)²=1.

B. x²+ (y-1)²+ (z-1)²=1

C. (x-1)²+ (y-1)²+z²=1

D. (x-1)²+y²+ (z-1)²=1.

Xem lời giải »

Câu 3:

Trong không gian Oxyz, Cho mặt phẳng (R): x+y-2z+2=0 và đường thẳng $∆_{1} : \frac{x}{2} = \frac{y}{1} = \frac{z - 1}{- 1}$ .Đường thẳng Δ₂ nằm trong mặt phẳng (R) đồng thời cắt và vuông góc với đường thẳng Δ₁ có phương trình là:

Xem lời giải »

Câu 4:

Trong không gian Oxyz, mặt phẳng (α) đi qua M (1;1;4) cắt các tia Ox, Oy, Oz lần lượt tại A, B, C phân biệt sao cho tứ diện OABC có thể tích nhỏ nhất. Tính thể tích nhỏ nhất đó.

A. 72.

B. 108

B. 18.

D. 36.

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{1} = \frac{y}{- 1} = \frac{z - 2}{1}$ và mặt phẳng (P): 2x-y-2z+1=0. Đường thẳng nằm trong (P), cắt và vuông góc với d có phương trình là:

Xem lời giải »

Câu 6:

Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng $∆ : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 1}{- 2}$ đồng thời tiếp xúc với hai mặt phẳng (α₁): 2x+2y+z-6=0 và (α₂): x-2y+2z=0

A. 1

B. 0.

C. Vô số

D. 2.

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;0;1), B (0;1;-1). Hai điểm D, E thay đổi trên các đoạn OA, OB sao cho đường thẳng DE chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi DE ngắn nhất thì trung điểm của đoạn DE có tọa độ là:

Xem lời giải »

Câu 8:

Trong hệ tọa độ Oxyz cho A (3;3;0), B (3;0;3), C (0;3;3). Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:

A. x+y-2z=0.

B. x+y+2z=0.

C. x-z=0.

D. y-z=0

Xem lời giải »

Câu 9:

Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là:

A. (P):x+2y+3z+6=0.

B. (P):x+2y+z-2=0.

C. (P):x-2y+z-6=0.

D. (P):3x+2y+2z-4=0.

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2;0;0), B (0;3;0), C (0;0;6), D (1;1;1). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D?

A. 6

B. 10

C. 7

D. 5.

Xem lời giải »

Câu 11:

Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;-1;2). Biết rằng có hai mặt phẳng cùng đi qua hai điểm A, O và cùng cách B một khoảng bằng $\sqrt{3}$ . Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt phẳng đó.

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): 2y-z+3=0 và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:

A. 8.

B. 16

C. 8/3

D. 16/3

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x + 1}{2} = \frac{y - 1}{1} = \frac{z - 2}{3}$ và mặt phẳng (P):x-y-z-1=0. Phương trình đường thẳng Δ đi qua A (1;1;-2), song song với mặt phẳng (P) và vuông góc với đường thẳng d là:

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng (P): x+y-z-3=0. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng $\frac{\sqrt{17}}{2}$ . Tính bán kính R của mặt cầu (S).

A. R=3.

B. R=9

C. R=1

D. R=5.

Xem lời giải »

Câu 15:

Cho hình chóp S. ABCD có đáy ABCD là hình vuông có độ dài đường chéo bằng a $\sqrt{2}$ và SA vuông góc với mặt phẳng (ABCD). Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Nếu tan α = $\sqrt{2}$ thì góc giữa hai mặt phẳng (SAC) và (SBC) bằng:

A. 30⁰

B. 60⁰

C. 45⁰

D. 90⁰

Xem lời giải »

Câu 16:

Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P): 2x-y+2z+1=0. Đường thẳng $d : \frac{x + 2}{4} = \frac{y - 1}{- 4} = \frac{z + 2}{3}$ Tính T = m² - n².

A. T = -5.

B. T = 4.

C. T = 3

D. T = -4.

Xem lời giải »

Câu 17:

Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác ABC và thể tích khối tứ diện OABC bằng 3/2. Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng:

A. 3.

B. 2.

C. 4.

D. 1.

Xem lời giải »

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có phương trình đường phân giác trong góc A là: $\frac{x}{1} = \frac{y - 6}{- 4} = \frac{z - 6}{- 3}$ . Biết rằng điểm M (0;5;3) thuộc đường thẳng AB và điểm N (1;1;0) thuộc đường thẳng AC. Vectơ nào sau đây là vectơ chỉ phương của đường thẳng AC.

Xem lời giải »

Câu 19:

Trong không gian Oxyz, phương trình mặt phẳng (P) song song và cách đều hai đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}$ , $d_{2} : \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$ là?

A. (P):2y-2z+1=0.

B. (P):2x-2z+1=0.

C. (P):2x-2y+1=0.

D. (P):2y-2z-1=0.

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho điểm A (3;1;0), B (-9;4;9) và mặt phẳng (P) có phương trình 2x-y+z+1=0. Gọi I (a;b;c) là điểm thuộc mặt phẳng (P) sao cho |IA - IB| đạt giá trị lớn nhất. Khi đó tổng a+b+c bằng:

A. -4

B. 22

C. 13.

D. -13.

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+y²+ (z+2)²=4 và đường thẳng $d : \{\begin{cases} x = 2 - y y = t \\ z = m - 1 + t \end{cases}$ . Gọi T là tập tất cả các giá trị của m để d cắt (S) tại hai điểm phân biệt A, B sao cho các tiếp diện của (S) tại A và B tạo với nhau góc lớn nhất có thể. Tính tổng các phần tử của tập hợp T.

A. 3

B. -3

C. -5.

D. -4.

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (3; - 2; 3), B (- 1; 2; 5)$ . Tìm tọa độ trung điểm I của đoạn thẳng AB.

A. $I (- 2; 2; 1)$

B. $I (1; 0; 4)$

C. $I (2; 0; 8)$

D. $I (2; - 2; - 1)$

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(a;b;c). Mệnh đề nào sau đây là sai?

A. Điểm M thuộc Oz khi và chỉ khi a = b = 0.

B. Khoảng cách từ M đến (Oxy) bằng c.

C. Tọa độ hình chiếu của M lên Ox là (a;0;0)

D. Tọa độ $\vec{O M}$ là (a;b;c)

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \{\begin{matrix} x = 1 \\ y = 2 + 3 t \\ z = 5 - t \end{matrix} (t \in R)$ . Véc tơ nào dưới đây là vec tơ chỉ phương của d?

A. $\vec{u_{1}} = (0; 3; - 1)$

B. $\vec{u_{2}} = (1; 3; - 1)$

C. $\vec{u_{3}} = (1; - 3; - 1)$

D. $\vec{u_{4}} = (1; 2; 5)$

Xem lời giải »

Câu 4:

Cho hai vec tơ $\vec{u} = (- 2; 3; 1)$ và $\vec{v} = (1; 1; 1)$ . Khi đó số thực $m = \vec{u} . \vec{v}$ thỏa mãn

A. m = 0

B. $m \in (0; 2)$

C. $m \in (- 2; 0)$

D. $m \in (1; 3)$

Xem lời giải »

Câu 5:

Tung độ của điểm M thỏa mãn $\vec{O M} = 2 \vec{j} - \vec{i} + \vec{k}$ là:

A. -1

B. 1

C. 2

D. -2

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho điểm M thỏa mãn hệ thức $\vec{O M} = 2 \vec{i} + \vec{j}$ . Tọa độ điểm M là:

A. M(1;2;0)

B. M(2;1;0)

C. M(2;0;1)

D. M(0;2;1)

Xem lời giải »

Câu 7:

Điểm N là hình chiếu của M(x;y;z) trên trục toạ độ Oz thì:

A. N(x;y;z)

B. N(x;y;0)

C. N(0;0;z)

D. N(0;0;1)

Xem lời giải »

Câu 8:

Hình chiếu của điểm M(1;-1;0) lên trục Oz là:

A. N(-1;-1;0)

B. N(1;-1;0)

C. N(-1;1;0)

D. N(0;0;0)

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa Oxyz, cho điểm A(2;-3;5). Tọa độ điểm A’ là đối xứng của điểm A qua trục Oz là:

A. $(2; 3; 5)$

B. $(2; - 3; - 5)$

C. $(- 2; 3; 5)$

D. $(- 2; - 3; 5)$

Xem lời giải »

Câu 10:

Điểm $M \in (O x y)$ thì tọa độ điểm M là:

A. $M (x; y; 0)$

B. $M (0; x; y)$

C. $M (0; 0; z)$

D. $M (0; 0; 1)$

Xem lời giải »

Câu 11:

Trong không gian Oxyz, cho điểm M(1;0;2). Mệnh đề nào sau đây đúng?

A. $M \in (O x z)$

B. $M \in (O y z)$

C. $M \in O y$

D. $M \in (O x y)$

Xem lời giải »

Câu 12:

Trong không gian Oxyz, cho điểm M(1;2;3). Hình chiếu vuông góc của M trên (Oxz) là điểm nào sau đây.

A. $K (0; 2; 3)$

B. $H (1; 2; 0)$

C. $F (0; 2; 0)$

D. $E (1; 0; 3)$

Xem lời giải »

Câu 13:

Tọa độ trọng tâm tam giác AOB với A(1;2;-1) và B(2;1;0) là:

A. (1;1;-1)

B. (-1;1;-1)

C. $(1; 1; - \frac{1}{3})$

D. (3;3;-1)

Xem lời giải »

Câu 14:

Trong không gian Oxyz cho vec tơ $\vec{a} (2; - 2; 4)$ và $\vec{b} = 2 \vec{a}$ có tọa độ là

A. $(4; - 4; - 8)$

B. $(4; - 4; 8)$

C. $(1; - 1; 2)$

D. $(4; 4; 8)$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho vec tơ $\vec{a} (1; - 2; 0)$ và $\vec{b} = 2 \vec{a}$ . Tìm tọa độ của vec tơ $\vec{b}$

A. $\vec{b} = (2; 4; 2)$

B. $\vec{b} = (2; - 4; 0)$

C. $\vec{b} = (3; 0; 2)$

D. $\vec{b} = (2; 4; 0)$

Xem lời giải »

Câu 1:

Cho điểm G(1;1;2) là trọng tâm tam giác ABC với A(2;1;3), B(2;2;1). Chọn kết luận đúng về điểm C.

A. $C \in O y$

B. $C \in (O x z)$

C. $C \in O z$

D. $C \in (O y z)$

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ $(O; \vec{i}; \vec{j}; \vec{k})$ , cho hai vec tơ $\vec{a} = (2; - 1; 4), \vec{b} = \vec{i} - 3 \vec{k}$ .Tính $\vec{a} . \vec{b}$

A. -11

B. -13

C. 5

D. -10

Xem lời giải »

Câu 3:

Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm $A (1; 3; - 2)$ và song song với mặt phẳng $(P) : 2 x - y + 3 z + 4 = 0$ là:

A. $2 x - y + 3 z + 7 = 0$

B. $2 x + y - 3 z + 7 = 0$

C. $2 x + y + 3 z + 7 = 0$

D. $2 x - y + 3 z - 7 = 0$

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz, đường thẳng $Δ : \frac{x}{1} = \frac{y}{1} = \frac{z}{2}$ vuông góc với mặt phẳng nào trong các mặt phẳng sau?

A. $(P) : x + y + z = 0$

B. $(β) : x + y - z = 0$

C. $(β) : x + y - z = 0$

D. $(Q) : x + y - 2 z = 0$

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (1; - 2; - 1), B (1; 0; 2)$ và $C (0; 2; 1)$ . Viết phương trình mặt phẳng qua A và vuông góc với đường thẳng BC.

A. $x - 2 y + z - 4 = 0$

B. $x - 2 y - z + 4 = 0$

C. $x - 2 y - z - 6 = 0$

D. $x - 2 y + z + 4 = 0$

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) qua điểm $A (1; - 3; 2)$ và vuông góc với hai mặt phẳng $(α) : x + 3 = 0, (β) : z - 2 = 0$ có phương trình là:

A. $y + 3 = 0$

B. $y - 2 = 0$

C. $2 y - 3 = 0$

D. $2 x - 3 = 0$

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, gọi M, N, P lần lượt là hình chiếu vuông góc của A(2;-1;1) lên các trục Ox, Oy, Oz. Mặt phẳng đi qua A và song song với mặt phẳng (MNP) có phương trình là

A. $x - 2 y + 2 z - 2 = 0$

B. $x - 2 y + 2 z - 6 = 0$

C. $x - 2 y - 4 = 0$

D. $x + 2 z - 4 = 0$

Xem lời giải »

Câu 8:

Trong không gian, với hệ tọa độ Oxyz, cho ba điểm $A (2; - 1; 0), B (- 1; 2; - 2)$ và $C (3; 0; - 4)$ . Viết phương trình đường trung tuyến đỉnh A của tam giác ABC.

A. $\frac{x - 2}{1} = \frac{y + 1}{1} = \frac{z}{- 3}$

B. $\frac{x - 2}{1} = \frac{y + 1}{- 2} = \frac{z}{3}$

C. $\frac{x - 2}{1} = \frac{y + 1}{- 2} = \frac{z}{- 3}$

D. $\frac{x - 2}{- 1} = \frac{y + 1}{- 2} = \frac{z}{3}$

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, gọi $Δ$ là giao tuyến của hai mặt phẳng $x - y + 3 z - 1 = 0$ và $3 x - 7 z + 2 = 0$ . Một vec tơ chỉ phương của $Δ$ là:

A. $\vec{u} = (7; 16; 3)$

B. $\vec{u} = (7; 0; - 3)$

C. $\vec{u} = (- 4; 1; - 3)$

D. $\vec{u} = (0; - 16; 3)$

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu có tâm $I (1; 2; - 1)$ và tiếp xúc với mặt phẳng $(P) : x - 2 y - 2 z - 8 = 0$

A. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 3$

B. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 3$

C. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 9$

D. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 9$

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng $(P) : 3 x + y + z - 4 = 0$ , $(Q) : 3 x + y + z + 5 = 0$ , $(R) : 2 x - 3 y - 3 z + 1 = 0$ . Xét các mệnh đề $(1) : (P) / / (Q)$ và $(2) : (P) ⊥ (R)$ . Khẳng định nào sau đây đúng?

A. (1) đúng, (2) sai

B. (1) sai, (2) đúng

C. (1) đúng, (2) đúng

D. (1) sai, (2) sai

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, tìm tất cả các giá trị thực của m để đường thẳng $Δ : \frac{x - 1}{2} = \frac{y + 2}{- 1} = \frac{z + 1}{1}$ song song với mặt phẳng $(P) : x + y - z + m = 0$

A. $m \neq 0$

B. $m = 0$

C. $m \in R$

D. Không có giá trị nào của m

Xem lời giải »

Câu 13:

Trong không gian với hệ trục Oxyz, cho đường thẳng $d : x - 1 = \frac{y - 2}{2} = \frac{z - 4}{3}$ và mặt phẳng $(P) : x + 4 y + 9 z - 9 = 0$ . Giao điểm I của d và (P) là:

A. $I (2; 4; - 1)$

B. $I (1; 2; 0)$

C. $I (1; 0; 0)$

D. $I (0; 0; 1)$

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(α) : x - y + 2 z + 1 = 0$ và đường thẳng $Δ : \frac{x}{1} = \frac{y}{2} = \frac{z - 1}{- 1}$ . Góc giữa đường thẳng $∆$ và mặt phẳng $(α)$ bằng:

A. $30 °$

B. $60 °$

C. $150 °$

D. $120 °$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y=0. Trong bốn mặt phẳng sau, mặt phẳng nào vuông góc với mặt phẳng (P)?

A. $(P_{1}) : x - 2 y + z - 1 = 0$

B. $(P_{3}) : 2 x - y + z - 1 = 0$

C. $(P_{2}) : x - y + z - 1 = 0$

D. $(P_{4}) : - 2 x - y = 0$

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;3;1), B(5;6;2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tính tỉ số $\frac{A M}{B M}$

A. $\frac{A M}{B M} = \frac{1}{2}$

B. $\frac{A M}{B M} = 2$

C. $\frac{A M}{B M} = \frac{1}{3}$

D. $\frac{A M}{B M} = 3$

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, gọi $(α)$ là mặt phẳng chứa đường thẳng $∆$ có phương trình $\frac{x - 2}{1} = \frac{y - 1}{1} = \frac{z}{2}$ và vuông góc với mặt phẳng $(β) : x + y - 2 z - 1 = 0$ . Giao tuyến của $(α)$ và $(β)$ đi qua điểm nào trong các điểm sau:

A. $A (2; 1; 1)$

B. $C (1; 2; 1)$

C. $D (2; 1; 0)$

D. $B (0; 1; 0)$

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}, d {}_{2}: \frac{x}{2} = \frac{y - 1}{- 1} = \frac{z - 2}{- 1}$

A. $(P) : 2 x - 2 z + 1 = 0$

B. $(P) : 2 y - 2 z + 1 = 0$

C. $(P) : 2 x - 2 y + 1 = 0$

D. $(P) : 2 y - 2 z - 1 = 0$

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng $(α)$ chắn các trục Ox, Oy, Oz lần lượt tại A, B, C sao cho H(3;-4;2) là trực tâm của tam giác ABC. Phương trình mặt phẳng $(α)$ là:

A. $2 x - 3 y + 4 z - 26 = 0$

B. $x - 3 y + 2 z - 17 = 0$

C. $4 x + 2 y - 3 z + 2 = 0$

D. $3 x - 4 y + 2 z - 29 = 0$

Xem lời giải »

Câu 5:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(3;3;-2) và hai đường thẳng $d_{1} : \frac{x - 1}{1} = \frac{y - 2}{3} = \frac{z}{1}, d_{2} : \frac{x - 1}{- 1} = \frac{y - 1}{2} = \frac{z - 2}{4}$ . Đường thẳng d qua M cắt $d_{1}, d_{2}$ lần lượt tại A và B. Tính độ dài đoạn thẳng AB.

A. AB = 1

B. AB = 3

C. $A B = \sqrt{6}$

D. $A B = \sqrt{5}$

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I thuộc đường thẳng $Δ : \frac{x}{1} = \frac{y + 3}{1} = \frac{z}{2}$ . Biết rằng mặt cầu (S) có bán kính bằng $2 \sqrt{2}$ và cắt mặt phẳng (Oxz) theo một đường tròn có bán kính bằng 2. Tìm tọa độ của điểm I.

A. $I (5; 2; 10), I (0; - 3; 0)$

B. $I (1; - 2; 2), I (0; - 3; 0)$

C. $I (1; - 2; 2), I (5; 2; 10)$

D. $I (1; - 2; 2), I (- 1; 2; - 2)$

Xem lời giải »

Câu 7:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;1;2), mặt phẳng (P) qua M cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C (A, B, C có tọa độ dương). Gọi $V_{O A B C}$ là thể tích tứ diện OABC. Khi (P) thay đổi tìm giá trị nhỏ nhất của $V_{O A B C}$

A. $\min V_{O A B C} = \frac{9}{2}$

B. $\min V_{O A B C} = 18$

C. $\min V_{O A B C} = 9$

D. $\min V_{O A B C} = \frac{32}{3}$

Xem lời giải »

Câu 8:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm $A (2; 3; 0), B (0; - \sqrt{2}, 0), M (\frac{2}{5}; - \sqrt{2}; - \frac{2}{5})$ và đường thẳng $d : \{\begin{matrix} x = t \\ y = 0 \\ z = 2 - t \end{matrix}$ . Điểm C thuộc d sao cho chu vi tam giác ABC là nhỏ nhất thì độ dài CM bằng

A. $2 \sqrt{2}$

B. 4

C. 2

D. $\frac{2 \sqrt{6}}{5}$

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 6 x - 4 z + 9 - m^{2} = 0$ . Gọi T là tập các giá trị của m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz). Tích các giá trị của m trong T bằng:

A. -5

B. 5

C. 0

D. 4

Xem lời giải »

Câu 10:

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x - 1}{- 2} = \frac{y}{2} = \frac{z - 2}{1}$ và mặt phẳng $(P) : 2 x - y + z - 3 = 0$ . Gọi (S) là mặt cầu có tâm I thuộc $∆$ và tiếp xúc với (P) tại điểm $H (1; - 1; 0)$ . Phương trình của (S) là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 36$

B. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 36$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 6$

D. ${(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 6$

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 8 x + 2 y + 2 z - 3 = 0$ và đường thẳng $Δ : \frac{x - 1}{3} = \frac{y}{- 2} = \frac{z + 2}{- 1}$ . Mặt phẳng $(α)$ vuông góc với $Δ$ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình $(α)$ là:

A. $3 x - 2 y - z - 5 = 0$

B. $3 x - 2 y - z + 5 = 0$

C. $3 x - 2 y - z + 15 = 0$

D. $3 x - 2 y - z - 15 = 0$

Xem lời giải »

Câu 12:

Trong không gian Oxyz, cho điểm S(-2;1;-2) nằm trên mặt cầu $(S) : x^{2} + y^{2} + z^{2} = 9$ . Từ điểm S kẻ dây cung SA, SB, SC với mặt cầu (S) có độ dài bằng nhau và đôi một tạo với nhau góc $60 °$ . Dây cung AB có độ dài bằng:

A. $2 \sqrt{6}$

B. $2 \sqrt{3}$

C. $\sqrt{3}$

D. $\sqrt{6}$

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho điểm E(2;1;3), mặt phẳng $(P) : 2 x + 2 y - z - 3 = 0$ và mặt cầu $(S) : {(x - 3)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 36$ . Gọi $Δ$ là đường thẳng đi qua E, nằm trong (P) và cắt (S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của $Δ$ là:

A. $\{\begin{matrix} x = 2 + 9 t \\ y = 1 + 9 t \\ z = 3 + 8 t \end{matrix}$

B. $\{\begin{matrix} x = 2 - 5 t \\ y = 1 + 3 t \\ z = 3 \end{matrix}$

C. $\{\begin{matrix} x = 2 + t \\ y = 1 - t \\ z = 3 \end{matrix}$

D. $\{\begin{matrix} x = 2 + 4 t \\ y = 1 + 3 t \\ z = 3 - 3 t \end{matrix}$

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho hình hộp ABCD.A’B’C’D’ biết $A (1; 0; 1), B (2; 1; 2), D (2; - 2; 2), A' (3; 0; - 1)$ . Điểm M thuộc cạnh DC. GTNN của tổng các khoảng cách $A M + M C'$ là:

A. $\sqrt{17}$

B. $\sqrt{17 + 4 \sqrt{6}}$

C. $\sqrt{17 + 8 \sqrt{3}}$

D. $\sqrt{17 + 6 \sqrt{2}}$

Xem lời giải »

Câu 15:

Trong không gian Oxyz, cho hai điểm A(0;-1;2), B(1;1;2) và đường thẳng d: $\frac{x + 1}{1} = \frac{y}{1} = \frac{z - 1}{1}$ . Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị $\frac{x + 1}{1} = \frac{y}{1} = \frac{z - 1}{1}$ bằng:

A. 10

B. 5

C. 3

D. 4

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + {(y + 1)}^{2} + z^{2} = R^{2}$ . Điều kiện của bán kính R để trục Ox tiếp xúc với (S) là:

A. R = 4

B. R = 2

C. $R = \pm 1$

D. R = 1

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.

A. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 25$

B. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

C. $(S) : {(x + 3)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 20$

D. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 5$

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$ . Tính đường kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d.

A. $5 \sqrt{2}$

B. $10 \sqrt{2}$

C. $2 \sqrt{5}$

D. $4 \sqrt{5}$

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình $\{\begin{matrix} x = - 1 + 2 t \\ y = 2 + t \\ z = - 3 - t \end{matrix} (t \in R)$ . Mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d có bán kính là:

A. $5 \sqrt{2}$

B. $10 \sqrt{2}$

C. $2 \sqrt{5}$

D. $4 \sqrt{5}$

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm $I (2; 0; 1)$ và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$ là:

A. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 2$

B. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 24$

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $Δ$ có phương trình x=y=z. Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu không có hai điểm chung phân biệt với $Δ$ là:

A. $x^{2} + y^{2} + z^{2} + x + y + z - 6 = 0$

B. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 2 z - 3 = 0$

C. $x^{2} + y^{2} + z^{2} - 2 x + 3 y + 5 z + 3 = 0$

D. $x^{2} + y^{2} + z^{2} - 7 x - 2 z + 6 = 0$

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{1} = \frac{y + 1}{1} = \frac{z - m}{2}$ và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 9$ . Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt E, F sao cho độ dài đoạn thẳng EF lớn nhất.

A. m = 1

B. $m = - \frac{1}{3}$

C. m = 0

D. $m = \frac{1}{3}$

Xem lời giải »

Câu 8:

Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu có điểm chung với trục Oz là:

A. $x^{2} + y^{2} + z^{2} + 4 x - 8 y + 2 z + 2 = 0$

B. $x^{2} + y^{2} + z^{2} + 2 x - 4 y - 2 z + 2 = 0$

C. $x^{2} + y^{2} + z^{2} + x - 2 y + z + 1 = 0$

D. $x^{2} + y^{2} + z^{2} - 2 x + 4 y + 4 z + 4 = 0$

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + {(y + 2)}^{2} + z^{2} = 5$ . Tìm tất cả các giá trị thực của tham số m để đường thẳng $Δ : \frac{x - 1}{2} = \frac{y + m}{1} = \frac{z - 2 m}{- 3}$ cắt (S) tại hai ddiemr phân biệt A, B sao cho A, B có độ dài AB lớn nhất

A. $m = - \frac{1}{2}$

B. $m = \pm \frac{1}{3}$

C. $m = \frac{1}{3}$

D. m = 0

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 50$ . Trong số các đường thẳng sau. Mặt cầu (S) tiếp xúc với đường nào.

A. $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$

B. Trục Ox

C. Trục Oy

D. Trục Oz

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.

A. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 25$

B. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

C. $(S) : {(x + 3)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 20$

D. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 5$

Xem lời giải »

Câu 12:

Xét đường thẳng d có phương trình $\{\begin{matrix} x = 1 + t \\ y = 2 \\ z = 3 + 2 t \end{matrix}$ và mặt cẩu (S) có phương trình ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 4$ . Nhận xét nào sau đây đúng.

A. d cắt (S) tại hai điểm phân biệt A, B và AB < 2R.

B. d không có điểm chung với (S)

C. d tiếp xúc với (S)

D. D cắt (S) tại hai điểm phân biệt A, B và AB đạt GTNN

Xem lời giải »

Câu 13:

Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng $Δ : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 1}{- 2}$ đồng thời tiếp xúc với hai mặt phẳng $(α_{1}) : 2 x + 2 y + z - 6 = 0$ và $(α_{2}) : x - 2 y + 2 z = 0$

A. 1

B. 0

C. Vô số

D. 2

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 9$ và đường thẳng $d : x - 1 = \frac{y - 2}{2} = \frac{z - 4}{3}$ . (d) cắt (S) tại hai điểm phân biệt A và B. Khi đó AB bằng:

A. $A B = \frac{\sqrt{126}}{7}$

B. $A B = \frac{\sqrt{123}}{7}$

C. $A B = \sqrt{\frac{126}{7}}$

D. $A B = \sqrt{\frac{129}{7}}$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;-2;0) và cắt trục Oy tại hai điểm A, B mà AB = 8 là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 9$

B. ${(x + 3)}^{2} + {(y - 2)}^{2} + z^{2} = 25$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 64$

D. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 25$

Xem lời giải »

Câu 16:

Trong không gian Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 6$ tiếp xúc với hai mặt phẳng $(P) : x + y + 2 z + 5 = 0$ , $(Q) : 2 x - y + z - 5 = 0$ lần lượt tại các điểm A, B. Độ dài đoạn thẳng AB là:

A. $2 \sqrt{3}$

B. $\sqrt{3}$

C. $2 \sqrt{6}$

D. $3 \sqrt{2}$

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d : \{\begin{matrix} x = 2 t \\ y = t \\ z = 4 \end{matrix}$ và $d' : \{\begin{matrix} x = t' \\ y = 3 - t' \\ z = 0 \end{matrix}$ . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d’là:

A. ${(x - 2)}^{2} + y^{2} + z^{2} = 4$

B. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 2$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 2)}^{2} + {(y + 1)}^{2} + z^{2} = 4$

Xem lời giải »

Câu 18:

Trong không gian Oxyz, mặt phẳng $(P) : 2 x + 6 y + z - 3 = 0$ cắt trục Oz và đường thẳng $d : \frac{x - 5}{1} = \frac{y}{2} = \frac{z - 6}{- 1}$ lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:

A. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 36$

B. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 9$

C. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 9$

D. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 36$

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$ . Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz

A. ${(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

C. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 4$

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz. Hãy viết phương trình mặt cầu (S) có tâm $I (2; 0; 1)$ và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$

A. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 2$

B. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 24$

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y - 2}{1} = \frac{z + 1}{2}$ , điểm $A (2; - 1; 1)$ . Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

A. $x^{2} + {(y - 3)}^{2} + {(z - 1)}^{2} = 20$

B. $x^{2} + {(y + 1)}^{2} + {(z + 2)}^{2} = 5$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z + 3)}^{2} = 20$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 14$

Xem lời giải »

Câu 22:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 4 y + 4 z - 16 = 0$ và đường thẳng $d : \frac{x - 1}{1} = \frac{y + 3}{2} = \frac{z}{2}$ . Mặt phẳng nào trong các mặt phẳng sau chứa d và tiếp xúc với mặt cầu (S)

A. $(P) : 2 x - 2 y + z - 8 = 0$

B. $(P) : - 2 x + 11 y - 10 z - 105 = 0$

C. $(P) : 2 x - 11 y + 10 z - 35 = 0$

D. $(P) : - 2 x + 2 y - z + 11 = 0$

Xem lời giải »

Câu 23:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 6 x + 4 y - 2 z + 5 = 0$ . Phương trình mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là:

A. $(Q) : 2 y + z = 0$

B. $(Q) : 2 y - z = 0$

C. $(Q) : y - 2 z = 0$

D. $(Q) : 2 y - z = 0$

Xem lời giải »

Câu 24:

A. $I (1; - 2; 2), I (5; 2; 10)$

B. $I (1; - 2; 2), I (0; 3; 0)$

C. $I (5; 2; 10), I (0; - 3; 0)$

D. $I (1; - 2; 2), I (- 1; 2; - 2)$

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình: $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 2 z - 3 = 0$ và đường thẳng $Δ : \frac{x}{2} = \frac{y + 1}{- 2} = z$ . Mặt phẳng (P) vuông góc với $Δ$ và tiếp xúc với (S) có phương trình là

A. $2 x - 2 y + z - 2 = 0$ và $2 x - 2 y + z + 16 = 0$

B. $2 x - 2 y + z + 2 = 0$ và $2 x - 2 y + z - 16 = 0$

C. $2 x - 2 y - 3 \sqrt{8} + 6 = 0$ và $2 x - 2 y - 3 \sqrt{8} - 6 = 0$

D. $2 x - 2 y + 3 \sqrt{8} - 6 = 0$ và $2 x - 2 y - 3 \sqrt{8} - 6 = 0$

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \{\begin{matrix} x = t \\ y = - 1 \\ z = - t \end{matrix}$ và 2 mặt phẳng (P) và (Q) lần lượt có phương trình $x + 2 y + 2 z + 3 = 0; x + 2 y + 2 z + 7 = 0$ . Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng d, tiếp xúc với hai mặt phẳng (P) và (Q)

A. ${(x + 3)}^{2} + {(y + 1)}^{2} + {(z - 3)}^{2} = \frac{4}{9}$

B. ${(x - 3)}^{2} + {(y + 1)}^{2} + {(z + 3)}^{2} = \frac{4}{9}$

C. ${(x + 3)}^{2} + {(y + 1)}^{2} + {(z + 3)}^{2} = \frac{4}{9}$

D. ${(x - 3)}^{2} + {(y - 1)}^{2} + {(z + 3)}^{2} = \frac{4}{9}$

Xem lời giải »

Câu 2:

Trong khôn gian Oxyz, cho biết có hai mặt cầu có tâm nằm trên đường thẳng $d : \frac{x}{2} = \frac{y - 1}{1} = \frac{z + 2}{- 1}$ , tiếp xúc đồng thời với hai mặt phẳng $(α) : x + 2 y - 2 z + 1 = 0$ và $(β) : 2 x - 3 y - 6 z - 2 = 0$ . Gọi $R_{1}; R_{2} (R_{1} > R_{2})$ là bán kính của hai mặt cầu đó. Tỉ số $\frac{R_{1}}{R_{2}}$ bằng:

A. $\sqrt{2}$

B. 3

C. 2

D. $\sqrt{3}$

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x}{2} = \frac{z - 3}{1} = \frac{y - 2}{1}$ và hai mặt phẳng $(P) : x - 2 y + 2 z = 0; (Q) : x - 2 y + 3 z - 5 = 0$ . Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiêp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S)

A. $(S) : {(x + 2)}^{2} + {(y + 4)}^{2} + {(z + 3)}^{2} = \frac{2}{7}$

B. $(S) : {(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 3)}^{2} = \frac{9}{14}$

C. $(S) : {(x - 2)}^{2} + {(y - 4)}^{2} + {(z - 3)}^{2} = \frac{2}{7}$

D. $(S) : {(x + 2)}^{2} + {(y + 4)}^{2} + {(z + 3)}^{2} = \frac{9}{14}$

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho 3 điểm A(0;1;1), B(3;0;-1) và C(0;21;-19) mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 1$ . Điểm M thuộc mặt cầu (S) sao cho tổng $3 M A^{2} + 2 M B^{2} + M C^{2}$ đạt giá trị nhỏ nhất, khi đó, độ dài vec tơ $\vec{O M}$ là:

A. $\sqrt{110}$

B. $3 \sqrt{10}$

C. $\frac{3 \sqrt{10}}{5}$

D. $\frac{\sqrt{110}}{5}$

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-y-2z+1=0 và ba điểm $A (1; - 2; 0), B (1; 0; - 1), C (0; 0; - 2)$ . Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng (P) và tiếp xúc với ba đường thẳng AB. AC, BC?

A. 4 mặt cầu

B. 2 mặt cầu

C. 1 mặt cầu

D. Vô số mặt cầu

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho 3 điểm A(6;0;0), B(0;6;0), C(0;0;6). Hai mặt cầu có phương trình $(S_{1}) : x^{2} + y^{2} + z^{2} - 2 x - 2 y + 1 = 0$ và $(S_{2}) : x^{2} + y^{2} + z^{2} - 8 x + 2 y + 2 z + 1 = 0$ cắt nhau theo đường tròn (C). Hỏi có bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa (C) và tiếp xúc với ba đường thẳng AB, BC, CA?

A. 4

B. Vô số

C. 1

D. 3

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.

A. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 25$

B. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

C. $(S) : {(x + 3)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 20$

D. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 5$

Xem lời giải »

Câu 8:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;-1) tiếp xúc với mặt phẳng $(α)$ có phương trình $2 x - 2 y - z + 3 = 0$ . Bán kính của (S) là:

A. 2

B. $\frac{2}{3}$

C. $\frac{2}{9}$

D. $\frac{4}{3}$

Xem lời giải »

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(1;-2;3). Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:

A. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 10$

B. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 9$

C. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 8$

D. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 16$

Xem lời giải »

Câu 10:

Trong không gian Oxyz, cho điểm I(1;2;5) và mặt phẳng $(α) : x - 2 y + 2 z + 2 = 0$ . Phương trình mặt cầu tâm I và tiếp xúc với $(α)$ là:

A. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 3$

B. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z + 5)}^{2} = 3$

C. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 9$

D. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z + 5)}^{2} = 9$

Xem lời giải »

Câu 11:

Trong khôn gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;-1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. $x + y - 3 z - 8 = 0$

B. $x - y - 3 z + 3 = 0$

C. $x + y + 3 z - 9 = 0$

D. $x + y - 3 z + 3 = 0$

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y + 1)}^{2} + {(z + 2)}^{2} = 4$ và 2 đường thẳng $Δ_{1} : \{\begin{matrix} x = 2 t \\ y = 1 - t \\ z = t \end{matrix}$ và $Δ_{2} : \frac{x - 1}{- 1} = \frac{y}{1} = \frac{z}{- 1}$ . Một phương trình mặt phẳng (P) song song với $Δ_{1}, Δ_{2}$ và tiếp xúc với mặt cầu (S) là:

A. $x + z + 3 - 2 \sqrt{2} = 0$

B. $y + z - 3 - 2 \sqrt{2} = 0$

C. $x + y + 3 + 2 \sqrt{2} = 0$

D. $y + z + 3 + 2 \sqrt{2} = 0$

Xem lời giải »

Câu 13:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với $(S) : x^{2} + y^{2} + z^{2} - 2 x - 4 y - 6 z - 2 = 0$ và song song với $(α) : 4 x + 3 y - 12 z + 10 = 0$

A. $[\begin{matrix} 4 x + 3 y - 12 z + 26 = 0 \\ 4 x + 3 y - 12 z - 78 = 0 \end{matrix}$

B. $[\begin{matrix} 4 x + 3 y - 12 z - 26 = 0 \\ 4 x + 3 y - 12 z - 78 = 0 \end{matrix}$

C. $[\begin{matrix} 4 x + 3 y - 12 z + 26 = 0 \\ 4 x + 3 y - 12 z + 78 = 0 \end{matrix}$

D. $[\begin{matrix} 4 x + 3 y - 12 z - 26 = 0 \\ 4 x + 3 y - 12 z + 78 = 0 \end{matrix}$

Xem lời giải »

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0;-1;0), B(1;1;-1) và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 2 z - 3 = 0$ . Mặt phẳng (P) đi qua A, B và cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là:

A. $x - 2 y + 3 z - 2 = 0$

B. $x - 2 y - 3 z - 2 = 0$

C. $x + 2 y - 3 z - 6 = 0$

D. $2 x - y - 1 = 0$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) đi qua điểm $A (2; - 2; 5)$ tiếp xúc với các mặt phẳng $(α) : x = 1, (β) : y = - 1, (γ) : z = 1$ . Tính bán kính của mặt cầu (S):

A. $\sqrt{33}$

B. 1

C. $3 \sqrt{2}$

D. 3

Xem lời giải »

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 4)}^{2} = 10$ và mặt phẳng $(P) : - 2 x + y + \sqrt{5} z + 9 = 0$ . Gọi (Q) là tiết diện của (S) tại $M (5; 0; 4)$ . Tính góc giữa (P) và (Q)

A. $45 °$

B. $60 °$

C. $120 °$

D. $30 °$

Xem lời giải »

Câu 17:

Trong không gian Oxyz, xác định tọa độ tâm I của đường tròn giao tuyến của mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 64$ với mặt phẳng $(α) : 2 x + 2 y + z + 10 = 0$

A. $(- \frac{7}{3}; - \frac{7}{3}; - \frac{2}{3})$

B. $(- 2; - 2; - 2)$

C. $(- \frac{2}{3}; - \frac{7}{3}; - \frac{7}{3})$

D. $(- \frac{7}{3}; - \frac{2}{3}; - \frac{7}{3})$

Xem lời giải »

Câu 18:

Mặt phẳng (Oyz) cắt mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 2 y + 4 z - 3 = 0$ theo một đường tròn có tọa độ tâm là

A. $(- 1; 0; 0)$

B. $(0; - 1; 2)$

C. $(0; 2; - 4)$

D. $(0; 1; - 2)$

Xem lời giải »

Câu 19:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 4 y - 6 z = 0$ . Đường tròn giao tuyến của (S) với mặt phẳng (Oxy) có bán kính là:

A. $\sqrt{5}$

B. 4

C. $2 \sqrt{5}$

D. 5

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 2)}^{2} = 9$ và mặt phẳng $(P) : 2 x - y - 2 z + 1 = 0$ . Biết (P) cắt (S) theo giao tuyến là đường tròn có bán kính r. Tính r.

A. r = 3

B. $r = 2 \sqrt{2}$

C. $r = \sqrt{3}$

D. r = 2

Xem lời giải »

Câu 21:

Viết phương trình mặt cầu có tâm I(-1;2;3) và tiếp xúc với mặt phẳng $(P) : 2 x - y - 2 z + 1 = 0$

A. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 2$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 3$

C. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 4$

D. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 9$

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;0;-4) và tiếp xúc với mặt phẳng (Oxy). Phương trình mặt cầu (S) là:

A. ${(x - 1)}^{2} + y^{2} + {(z + 4)}^{2} = 4$

B. ${(x - 1)}^{2} + y^{2} + {(z + 4)}^{2} = 16$

C. ${(x - 1)}^{2} + y^{2} + {(z + 4)}^{2} = 1$

D. ${(x - 1)}^{2} + y^{2} + {(z + 4)}^{2} = 2$

Xem lời giải »

Câu 23:

Trong không gian Oxyz, mặt cầu (S) có tâm I(-2;5;1) và tiếp xúc với mặt phẳng $(P) : 2 x + 2 y - z + 7 = 0$ có phương trình là:

A. ${(x + 2)}^{2} + {(y - 5)}^{2} + {(z - 1)}^{2} = 16$

B. ${(x + 2)}^{2} + {(y - 5)}^{2} + {(z - 1)}^{2} = 4$

C. ${(x + 2)}^{2} + {(y - 5)}^{2} + {(z - 1)}^{2} = \frac{25}{9}$

D. ${(x - 2)}^{2} + {(y + 5)}^{2} + {(z + 1)}^{2} = 16$

Xem lời giải »

Câu 24:

Một quả cầu (S) có tâm I(-1;2;1) và tiếp xúc với mặt phẳng $(P) : x - 2 y - 2 z - 2 = 0$ có phương trình là:

A. $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 3$

B. $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 3$

C. $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 9$

D. $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 9$

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm $A (1; 2; 1), B (3; 2; 3)$ , có tâm thuộc mặt phẳng $(P) : x - y - 3 = 0$ , đồng thời có bán kính nhỏ nhất, hãy tính bán kính R của mặt cầu (S)?

A. 1

B. $\sqrt{2}$

C. 2

D. $2 \sqrt{2}$

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, $(α)$ cắt mặt cầu (S) tâm I(1;-3;3) theo giao tuyến là đường tròn tâm H(2;0;1), bán kính r = 2. Phương trình (S) là:

A. ${(x - 1)}^{2} + {(y + 3)}^{2} + {(z - 3)}^{2} = 18$

B. ${(x + 1)}^{2} + {(y - 3)}^{2} + {(z + 3)}^{2} = 4$

C. ${(x - 1)}^{2} + {(y + 3)}^{2} + {(z - 3)}^{2} = 4$

D. ${(x + 1)}^{2} + {(y - 3)}^{2} + {(z + 3)}^{2} = 18$

Xem lời giải »

Câu 2:

Trong không gian Oxyz, cho I(2;1;1) và mặt phẳng $(P) : 2 x + y + 2 z - 1 = 0$ . Mặt cầu (S) có tâm I cắt (P) theo một đường tròn có bán kính r = 4. Phương trình của mặt cầu (S) là:

A. ${(x + 2)}^{2} + {(y + 1)}^{2} + {(z + 1)}^{2} = 20$

B. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 18$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 20$

D. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 2 \sqrt{5}$

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3). Gọi (S) là mặt cầu chứa A, có tâm I thuộc tia Ox và bán kính 7. Phương trình mặt cầu (S) là:

A. ${(x - 3)}^{2} + y^{2} + z^{2} = 49$

B. ${(x + 7)}^{2} + y^{2} + z^{2} = 49$

C. ${(x - 7)}^{2} + y^{2} + z^{2} = 49$

D. ${(x + 5)}^{2} + y^{2} + z^{2} = 49$

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm $I (- 3; 2; - 4)$ và tiếp xúc với mặt phẳng (Oxz)?

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 4)}^{2} = 2$

B. ${(x + 3)}^{2} + {(y - 2)}^{2} + {(z + 4)}^{2} = 9$

C. ${(x + 3)}^{2} + {(y - 2)}^{2} + {(z + 4)}^{2} = 4$

D. ${(x - 3)}^{2} + {(y + 2)}^{2} + {(z - 4)}^{2} = 16$

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (a; 0; 0), B (0; b; 0), C (0; 0; c)$ với $a, b, c > 0$ . Biết rằng (ABC) đi qua điểm $M (\frac{1}{7}; \frac{2}{7}; \frac{3}{7})$ và tiếp xúc với mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = \frac{72}{7}$ . Tính $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}$

A. $\frac{7}{2}$

B. $\frac{1}{7}$

C. 14

D. 7

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 25$ và mặt phẳng $(α) : 2 x + y - 2 z + m = 0$ . Tìm các giá trị của m để $(α)$ và (S) không có điểm chung.

A. m < -9 hoặc m > 21

B. -9 < m < 21

C. $- 9 \leq m \leq 21$

D. $m \leq - 9$

Xem lời giải »

Câu 7:

Mặt cầu (S) có tâm I(-1;2;-5) cắt mặt phẳng $(P) : 2 x - 2 y - z + 10 = 0$ theo thiết diện là hình tròn có diện tích $3 π$ . Phương trình của (S) là:

A. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 10 z + 18 = 0$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 5)}^{2} = 25$

C. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 5)}^{2} = 16$

D. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 10 z + 12 = 0$

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 a x - 2 b y - 2 c z + d = 0$ , với a, b, c đều là các số thực dương. Biết mặt cầu (S) cắt 3 mặt phẳng tọa độ $(Ox y), (O x z), (O y z)$ theo các giao tuyến là các đường tròn có bán kính bằng $\sqrt{13}$ và mặt cầu (S) đi qua $M (2; 0; 1)$ . Tính a+b+c

A. 6

B. 15

C. 3

D. 12

Xem lời giải »

Câu 9:

Trong không gian Oxyz, mặt cầu tâm I(1;2;-1) và cắt mặt phẳng $(P) : 2 x - y + 2 z - 1 = 0$ theo một đường tròn bán kính bằng $\sqrt{8}$ có phương trình là:

A. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 3$

B. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 9$

D. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2} = 3$

Xem lời giải »

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm $I (3; 2; - 1)$ và đi qua điểm $A (2; 1; 2)$ . Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?

A. $x + y - 3 z - 8 = 0$

B. $x - y - 3 z + 3 = 0$

C. $x + y + 3 z - 9 = 0$

D. $x + y - 3 z + 3 = 0$

Xem lời giải »

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $(P) : x - 2 y + 2 z - 3 = 0$ và mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y - 2 z + 5 = 0$ . Giả sử $M \in (P)$ và $N \in (S)$ sao cho $\vec{M N}$ cùng phương với vec tơ $\vec{u} = (1; 0; 1)$ và khoảng cách MN lớn nhất. Tính MN

A. 3

B. $1 + 2 \sqrt{2}$

C. $3 \sqrt{2}$

D. 14

Xem lời giải »

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y + 6 z + 5 = 0$ . Tiếp diện của (S) tại điểm $M (- 1; 2; 0)$ có phương trình là:

A. 2x + y = 0

B. x = 0

C. y = 0

D. z = 0

Xem lời giải »

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 9$ và mặt phẳng $(P) : 2 x - 2 y + z + 3 = 0$ . Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:

A. $a + b + c = 5$

B. $a + b + c = 6$

C. $a + b + c = 7$

D. $a + b + c = 8$

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 2 y + 4 z - 1 = 0$ và mặt phẳng $(P) : x + y - z - m = 0$ . Tìm tất cả m để (P) cắt (S) theo giao tuyến là một đường tròn có bán kính lớn nhất.

A. m = -4

B. m = 0

C. m = 4

D. m = 7

Xem lời giải »

Câu 15:

Cho điểm A(0;8;2) và mặt cầu (S) có phương trình $(S) : {(x - 5)}^{2} + {(y + 3)}^{2} + {(z - 7)}^{2} = 72$ và điểm B(1;1;-9). Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử $\vec{n} = (1; m; n)$ là vec tơ pháp tuyến của (P). Lúc đó:

A. $m n = \frac{276}{49}$

B. $m n = - \frac{276}{49}$

C. mn = 4

D. mn = -4

Xem lời giải »

Câu 16:

Một vec tơ chỉ phương của đường thẳng $\frac{x - 1}{2} = y = \frac{z + 1}{- 1}$ là:

A. $(1; 0; - 1)$

B. $(- 2; 1; 1)$

C. $(2; 0; - 1)$

D. $(2; 1; - 1)$

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho ba vec tơ $\vec{a} = (2; 3; - 5), \vec{b} = (0; - 3; 4), \vec{c} = (1; - 2; 3)$ . Tọa độ vec tơ $\vec{n} = 3 \vec{a} + 2 \vec{b} - \vec{c}$ là:

A. $\vec{n} = (5; 1; - 10)$

B. $\vec{n} = (7; 1; - 4)$

C. $\vec{n} = (5; 5; - 10)$

D. $\vec{n} = (5; - 5; - 10)$

Xem lời giải »

Câu 18:

Cho các vec tơ $\vec{a} = (1; 2; 3); \vec{b} = (- 2; 4; 1); \vec{c} = (- 1; 3; 4)$ . Vec tơ $\vec{v} = 2 \vec{a} - 3 \vec{b} + 5 \vec{c}$ là:

A. $\vec{v} = (7; 3; 23)$

B. $\vec{v} = (23; 7; 3)$

C. $\vec{v} = (7; 23; 3)$

D. $\vec{v} = (3; 7; 23)$

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-2;4). Hình chiếu vuông góc của A trên trục Oy là điểm:

A. $P (0; 0; 4)$

B. $Q (1; 0; 0)$

C. $N (0; - 2; 0)$

D. $M (0; - 2; 4)$

Xem lời giải »

Câu 20:

Trong không gian Oxyz, cho măt phẳng $(α) : 2 x + y - 2 z + 9 = 0$ và ba điểm $A (2; 1; 0), B (0; 2; 1), C (1; 3; - 1)$ . Điểm $M \in (α)$ sao cho $|2 \vec{M A} + 3 \vec{M B} - 4 \vec{M C}|$ đạt giá trị nhỏ nhất. Khẳng định nào sau đây đúng?

A. $x_{M} + y_{M} + z_{M} = 3$

B. $x_{M} + y_{M} + z_{M} = 4$

C. $x_{M} + y_{M} + z_{M} = 2$

D. $x_{M} + y_{M} + z_{M} = 1$

Xem lời giải »

Câu 21:

Trong không gian Oxyz, cho đường thẳng $Δ : \frac{x}{1} = \frac{y - 1}{1} = \frac{z}{1}$ và hai điểm $A (1; 2; - 5), B (- 1; 0; 2)$ . Biết điểm M thuộc $Δ$ sao cho biểu thức $T = |M A - M B|$ đạt GTLN là: $T_{\max}$ . Khi đó, $T_{\max}$ bằng bao nhiêu?

A. $T_{\max} = \sqrt{57}$

B. $T_{\max} = 3 \sqrt{6}$

C. $T_{\max} = 3$

D. $T_{\max} = 2 \sqrt{6} - 3$

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(-1;0;2) và đi qua điểm A(0;1;1). Xét các điểm B, C, D thuộc (S) sao cho AB, AC, AD đôi một vuông góc với nhau. Thể tích của khối tứ diện ABCD có giá trị lớn nhất bằng:

A. $\frac{8}{3}$

B. 4

C. $\frac{4}{3}$

D. 8

Xem lời giải »

Câu 23:

Trong không gian Oxyz, cho mặt cầu (S): ${(x - 2)}^{2} + {(y - 3)}^{2} + {(z + 1)}^{2} = 16$ và điểm $A (- 1; - 1; - 1)$ . Xét các điểm M thuộc (S) sao cho đường thẳng AM tiếp xúc với (S), M luôn thuộc mặt phẳng có phương trình là:

A. $3 x + 4 y - 2 = 0$

B. $3 x + 4 y + 2 = 0$

C. $6 x + 8 y + 11 = 0$

D. $6 x + 8 y - 11 = 0$

Xem lời giải »

Câu 24:

Cho hình lập phương ABCD.A’B’C’D’ có tâm O. Gọi I là tâm của hình vuông A’B’C’D’ và M là điểm thuộc đoạn thẳng OI sao cho $M O = \frac{1}{2} M I$ . Khi đó sin của góc tạo bởi mặt phẳng (MC’D’) và (MAB) bằng:

A. $\frac{17 \sqrt{13}}{65}$

B. $\frac{6 \sqrt{85}}{85}$

C. $\frac{7 \sqrt{85}}{85}$

D. $\frac{6 \sqrt{13}}{65}$

Xem lời giải »

Câu 25:

Trong không gian Oxyz, cho đường thẳng d: $\{\begin{matrix} x = 1 + 3 t \\ y = 1 + 4 t \\ z = 1 \end{matrix}$ . Gọi $∆$ là đường thẳng đi qua điểm $A (1; 1; 1)$ và có vec tơ chỉ phương $\vec{u} = (- 2; 1; 2)$ . Đường phân giác của góc nhọn tạo bởi đường thẳng d và $∆$ có phương trình là:

A. $\{\begin{matrix} x = 1 + 27 t \\ y = 1 + t \\ z = 1 + t \end{matrix}$

B. $\{\begin{matrix} x = - 18 + 19 t \\ y = - 6 + 7 t \\ z = 11 - 10 t \end{matrix}$

C. $\{\begin{matrix} x = - 18 + 19 t \\ y = - 6 + 7 t \\ z = - 11 - 10 t \end{matrix}$

D. $\{\begin{matrix} x = 1 - t \\ y = 1 + 17 t \\ z = 1 + 10 t \end{matrix}$

Xem lời giải »

Câu 1:

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Mặt phẳng (P) đi qua M và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C $(A, B, C \neq 0)$ sao cho thể tích của tứ diện OABC nhỏ nhất. Phương trình của mặt phẳng (P) là:

A. $\frac{x}{6} + \frac{y}{3} + \frac{z}{1} = 1$

B. $\frac{x}{3} + \frac{y}{6} + \frac{z}{9} = 1$

C. $\frac{x}{2} + \frac{y}{6} + \frac{z}{18} = 1$

D. $\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1$

Xem lời giải »

Câu 2:

Trong hệ tọa độ Oxyz, cho hai điểm A(1;5;0), B(3;3;6) và đường thẳng $(d) : \{\begin{matrix} x = - 1 + 2 t \\ y = 1 - t \\ z = 2 t \end{matrix}$ . Một điểm M thay đổi trên d. Biết giá trị nhỏ nhất của nửa chu vi tam giác MAB là số có dạng $\sqrt{a} + \sqrt{b}$ với a, b là các số nguyên. Khi đó:

A. $a + b = 40$

B. $a + b = 38$

C. $|a - b| = 10$

D. $|a - b| = 12$

Xem lời giải »

Câu 3:

Trong không gian Oxyz, cho điểm M(1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x’Ox, y’Oy, z’Oz lần lượt tại ba điểm phân biệt A, B, C sao cho $O A = O B = O C \neq 0$

A. 3

B. 2

C. 1

D. 4

Xem lời giải »

Câu 4:

Trong không gian Oxyz, cho mặt cầu (S): $x^{2} + y^{2} + z^{2} - 2 x - 4 y + 6 z - 13 = 0$ và đường thẳng $d : \frac{x + 1}{1} = \frac{y + 2}{1} = \frac{z - 1}{1}$ . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn $\hat{A M B} = 60 °, \hat{B M C} = 90 °; \hat{C M A} = 120 °$ có dạng M(a;b;c) với a < 0. Tổng $a + b + c$ bằng:

A. 2

B. -2

C. 1

D. $\frac{10}{3}$

Xem lời giải »

Câu 5:

Trong không gian Oxyz, cho điểm A(1;2;-1), đường thẳng $d : \frac{x - 1}{2} = \frac{y + 1}{1} = \frac{z - 2}{- 1}$ và mặt phẳng $(P) : x + y + 2 z + 1 = 0$ . Điểm B thuộc mặt phẳng (P) thỏa mãn đường thẳng AB vuông góc và cắt đường thẳng d. Tọa độ điểm B là:

A. $(6; - 7; 0)$

B. $(3; - 2; - 1)$

C. $(- 3; 8; - 3)$

D. $(0; 3; - 2)$

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho mặt cầu (S): ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 6$ , tiếp xúc với hai mặt phẳng $(P) : x + y + 2 z + 5 = 0, (Q) : 2 x - y + z - 5 = 0$ lần lượt tại các tiếp điểm A, B. Độ dài đoạn thẳng AB là:

A. $2 \sqrt{3}$

B. $\sqrt{3}$

C. $2 \sqrt{6}$

D. $3 \sqrt{2}$

Xem lời giải »

Câu 7:

Trong không gian Oxyz, cho hai đường thẳng $d : \{\begin{matrix} x = 1 + t \\ y = 2 - t \\ z = t \end{matrix}, d' : \{\begin{matrix} x = 2 t' \\ y = 1 + t' \\ z = 2 + t' \end{matrix}$ .

Đường thẳng $∆$ cắt d, d’ lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng $∆$ là:

A. $\frac{x}{2} = \frac{y - 3}{- 1} = \frac{z + 1}{- 3}$

B. $\frac{x - 2}{- 2} = \frac{y - 1}{1} = \frac{z - 1}{3}$

C. $\frac{x - 1}{- 2} = \frac{y - 2}{1} = \frac{z}{3}$

D. $\frac{x - 4}{- 2} = \frac{y}{- 1} = \frac{z - 2}{3}$

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho đường thẳng d: $\frac{x - 1}{1} = \frac{y - 1}{1} = \frac{z - m}{2}$ và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 9$ . Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt E, F sao cho độ dài đoạn thẳng EF lớn nhất.

A. m = 1

B. $m = - \frac{1}{3}$

C. m = 0

D. $m = \frac{1}{3}$

Xem lời giải »

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA=2a và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD. Tang của góc tạo bởi hai mặt phẳng (AMC) và (SBC) bằng:

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{5}}{5}$

C. $\frac{2 \sqrt{3}}{3}$

D. $\frac{2 \sqrt{5}}{5}$

Xem lời giải »

Câu 10:

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Khoảng cách giữa hai đường thẳng MN và B’D’ bằng:

A. $\sqrt{5} a$

B. $\frac{\sqrt{5} a}{5}$

C. 3a

D. $\frac{a}{3}$

Xem lời giải »

Câu 11:

Trong không gian Oxyz, cho mặt phẳng $(α) : x - z - 3 = 0$ và điểm M(1;1;1). Gọi A là điểm thuộc tia Oz, B là hình chiếu của A lên $(α)$ . Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB là:

A. $\frac{3 \sqrt{123}}{2}$

B. $\frac{\sqrt{123}}{2}$

C. $\frac{3 \sqrt{3}}{2}$

D. $3 \sqrt{3}$

Xem lời giải »

Câu 12:

A. $\frac{2 \sqrt{39}}{39}$

B. $\frac{\sqrt{13}}{13}$

C. $\frac{\sqrt{3}}{6}$

D. $\frac{2 \sqrt{39}}{13}$

Xem lời giải »

Câu 13:

Trong không gian Oxyz, cho hai điểm A(10;6;-2), B(5;10;-9) và mặt phẳng $(α) : 2 x + 2 y + z - 12 = 0$ . Điểm M di động trên mặt phẳng $(α)$ sao cho MA, MB luôn tạo với $(α)$ các góc bằng nhau. Biết rằng M luôn thuộc một đường tròn $(ω)$ cố định. Hoành độ của tâm đường tròn $(ω)$ bằng:

A. $\frac{9}{2}$

B. 2

C. 10

D. 4

Xem lời giải »

Câu 14:

Trong không gian Oxyz, cho mặt phẳng $(α) : 2 x + y - 2 z - 2 = 0$ , đường thẳng $d : \frac{x + 1}{1} = \frac{y + 2}{2} = \frac{z + 3}{2}$ và điểm $A (\frac{1}{2}; 1; 1)$ . Gọi $∆$ là đường thẳng nằm trong mặt phẳng $(α)$ , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng $∆$ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:

A. $\frac{7}{3}$

B. $\frac{7}{2}$

C. $\frac{\sqrt{21}}{2}$

D. $\frac{3}{2}$

Xem lời giải »

Câu 15:

Trong không gian với hệ tọa độ Oxyz, cho M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz tại A, B, C sao cho M là trọng tâm tam giác ABC. Phương trình mặt phẳng (P) là:

A. $x + y + z - 6 = 0$

B. $\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 0$

C. $3 x + 2 y + z - 14 = 0$

D. $\frac{x}{3} + \frac{y}{2} + \frac{z}{1} = 1$

Xem lời giải »

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (1; 0; 0), B (0; 2; 0), C (0; 0; 3)$ . Gọi M là điểm thay đổi trên mặt phẳng (ABC) và N là điểm trên tia OM sao cho OM.ON=1. Biết rằng N luôn thuộc mặt cầu cố định. Viết phương trình mặt cầu đó?

A. ${(x - \frac{36}{49})}^{2} + {(y - \frac{18}{49})}^{2} + {(z - \frac{12}{49})}^{2} = \frac{25}{49}$

B. ${(x - \frac{1}{2})}^{2} + {(y - \frac{1}{4})}^{2} + {(z - \frac{1}{6})}^{2} = \frac{49}{144}$

C. $x^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

D. $x^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

Xem lời giải »

Câu 17:

Trong không gian Oxyz, mặt phẳng (P): 2x+6y+z-3 = 0 cắt trục Oz và đường thẳng $d : \frac{x - 5}{1} = \frac{y}{2} = \frac{z - 6}{- 1}$ lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:

A. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 36$

B. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 9$

C. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 9$

D. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 36$

Xem lời giải »

Câu 18:

Trong không gian Oxyz, cho hai điểm A(-1;3;-2) và B(-3;7;-18) mặt phẳng $(P) : 2 x - y + z + 1 = 0$ . Điểm $M (a; b; c) \in (P)$ sao cho mặt phẳng (ABM) vuông góc với (P) và $M A^{2} + M B^{2} = 246$ . Tính $S = a + b + c$

A. 0

B. -1

C. 10

D. 13

Xem lời giải »

Câu 19:

Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là $\cup \frac{x - 3}{- 1} = \frac{y - 3}{2} = \frac{z - 2}{- 1}$ , phương trình đường phân giác trong của góc C là: $\frac{x - 2}{2} = \frac{y - 4}{- 1} = \frac{z - 2}{- 1}$ . Đường thẳng AB có vec tơ chỉ phương là:

A. $\vec{u_{3}} (2; 1; - 1)$

B. $\vec{u_{2}} (1; - 1; 0)$

C. $\vec{u_{4}} (0; 1; - 1)$

D. $\vec{u_{1}} (1; 2; 1)$

Xem lời giải »

Câu 20:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x + 2}{4} = \frac{y - 1}{- 4} = \frac{z + 2}{3}$ và mặt phẳng $(P) : 2 x - y + 2 z + 1 = 0$ . Đường thẳng $∆$ đi qua $E (- 2; 1; - 2)$ song song với (P) đồng thời tạo với d góc bé nhất. Biết rằng $∆$ có một vec tơ chỉ phương $\vec{u} (m; n; 1)$ . Tính $T = m^{2} - n^{2}$

A. T = -5

B. T = 4

C. T = 3

D. T = -4

Xem lời giải »

Câu 21:

Cho hình chóp S.ABCD có ABCD là hình bình hành, AB = 2a, BC = a, ABC = 1200. Cạnh bên $S D = a \sqrt{3}$ và SD vuông góc với mặt phẳng đáy. Tính sin của góc tạo bởi SB và mặt phẳng (SAC)

A. $\frac{3}{4}$

B. $\frac{\sqrt{3}}{4}$

C. $\frac{1}{4}$

D. $\frac{\sqrt{3}}{7}$

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác ABC và thể tích khối OABC bằng $\frac{3}{2}$ . Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng:

A. 3

B. 2

C. 4

D. 1

Xem lời giải »

Câu 23:

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A (0; 0; - 2), B (4; 0; 0)$ . Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:

A. $I (2; 0; - 1)$

B. $I (2; 0; 0)$

C. $I (0; 0; - 1)$

D. $I (\frac{4}{3}; 0; - \frac{2}{3})$

Xem lời giải »

Câu 24:

Trong không gian với hệ tọa độ Oxyz, cho $A (- 3; 0; 0), B (0; 0; 3), C (0; - 3; 0)$ và mặt phẳng $(P) : x + y + z - 3 = 0$ . Tìm trên (P) điểm M sao cho $|\vec{M A} + \vec{M B} - \vec{M C}|$ nhỏ nhất

A. $M (3; 3; - 3)$

B. $M (- 3; - 3; 3)$

C. $M (3; - 3; 3)$

D. $M (- 3; 3; 3)$

Xem lời giải »

Câu 25:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d : \frac{x + 2}{2} = \frac{y + 3}{5} = \frac{z - 4}{- 1}$ và $d' : \{\begin{matrix} x = 3 - t \\ y = 1 \\ z = 10 + t \end{matrix}$ . Hai điểm $A \in d, B \in'$ thỏa mãn đường thẳng AB vuông góc với cả hai đường thẳng d, d’. Có bao nhiêu mặt cầu tiếp xúc với đường thẳng d tại A và tiếp xúc với đường thẳng d’ tại B?

A. 2

B. 1

C. 0

D. Vô số

Xem lời giải »

Câu 1:

Trong không gian tọa độ Oxyz, cho mặt cầu (S): $x^{2} + y^{2} + z^{2} - 2 x - 2 y + 4 z - 20 = 0$ và mặt phẳng $(P) : x + y - z - m = 0$ . Tìm m để (P) cắt (S) theo giao tuyến là một đường tròn bán kính lớn nhất.

A. m = -4

B. m = 4

C. m = 7

D. m = 0

Xem lời giải »

Câu 2:

Trong không gian với hệ tọa độ Oxyz, gọi I(a;b;c) là tâm mặt cầu đi qua điểm A(1;-1;4) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính P=a-b+c

A. P = 6

B. P = 0

C. P = 3

D. P = 9

Xem lời giải »

Câu 3:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;0;1), B(3;2;1). Gọi C(5;3;7) thỏa mãn MA = MB và MB + MC đạt giá trị nhỏ nhất. Tính P = a + b + c

A. 4

B. 0

C. 2

D. 5

Xem lời giải »

Câu 4:

Trong không gian với hệ tọa độ Oxyz cho ba mặt phẳng $(P) : x - 2 y + z - 1 = 0$ , $(Q) : x - 2 y + z + 8 = 0$ và $(R) : x - 2 y + z - 4 = 0$ . Một đường thẳng d thay đổi cắt ba mặt phẳng (P); (Q); (R) lần lượt tại A, B, C. Đặt $T = \frac{A B^{2}}{4} + \frac{144}{A C}$ . Tìm giá trị nhỏ nhất của T.

A. min T = 108

B. $\min T = 54 \sqrt[3]{2}$

C. min T = 96

D. $\min T = 72 \sqrt[3]{2}$

Xem lời giải »

Câu 5:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với $A (1; 0; 0), B (3; 2; 4); C (0; 5; 4)$ . Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $|\vec{M A} + \vec{M B} + 2 \vec{M C}|$ nhỏ nhất

A. $M (1; 3; 0)$

B. $M (1; - 3; 0)$

C. $M (3; 1; 0)$

D. $M (2; 6; 0)$

Xem lời giải »

Câu 6:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (3; 0; 0), B (1; 2; 1)$ và $C (2; - 1; 2)$ . Biết mặt phẳng qua B, C và tâm mặt cầu nội tiếp tứ diện OABC có một vec tơ pháp tuyến là $(10; a; b)$ . Tổng a + b là:

A. -2

B. 1

C. 2

D. -1

Xem lời giải »

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và đường thẳng $d : \frac{x - 1}{1} = \frac{y}{- 2} = \frac{z - 1}{9}$ . Biết đường thẳng $∆$ qua A, cắt d và khoảng cách từ gốc tọa độ đến $∆$ nhỏ nhất, $∆$ có một vec tơ chỉ phương là (1;a;b). Tổng a + b là

A. $\frac{86}{5}$

B. $- \frac{86}{5}$

C. 17

D. -17

Xem lời giải »

Câu 8:

Trong không gian Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 1}{2} = \frac{y}{- 1} = \frac{z + 2}{1}$ và $d_{2} : \frac{x + 1}{1} = \frac{y - 1}{7} = \frac{z - 3}{- 1}$ . Đường vuông góc chung của $d_{1}$ và $d_{2}$ lần lượt cắt $d_{1}, d_{2}$ tại A và B. Diện tích tam giác OAB bằng:

A. $\frac{\sqrt{6}}{4}$

B. $\frac{\sqrt{6}}{2}$

C. $\sqrt{6}$

D. $\frac{\sqrt{3}}{2}$

Xem lời giải »

Câu 9:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 2}{1} = \frac{y - 1}{- 2} = \frac{z - 1}{2}$ và hai điểm $A (3; 2; 1), B (2; 0; 4)$ . Gọi $∆$ là đường thẳng qua A, vuông góc với d sao cho khoảng cách từ B đến $∆$ là nhỏ nhất. Gọi $\vec{u} = (2; b; c)$ là một vec to chỉ phương của $∆$ . Khi đó, $|\vec{u}|$ bằng:

A. $\sqrt{17}$

B. $\sqrt{5}$

C. $\sqrt{6}$

D. 3

Xem lời giải »

Câu 10:

Trong không gian Oxyz, cho 2 điểm A(1;2;-3), M(-2;-2;1) và đường thẳng $d : \frac{x + 1}{2} = \frac{y - 5}{2} = \frac{z}{- 1}$ . $∆$ là đường thẳng đi qua M và vuông góc với đường thẳng d đồng thời cách A một khoảng lớn nhất, khi đó $∆$ đi qua điểm nào trong các điểm sau:

A. $(- 1; - 2; 3)$

B. $(2; - 7; - 1)$

C. $(- 1; 2; 3)$

D. $(- 1; - 1; - 3)$

Xem lời giải »

Câu 11:

Trong không gian Oxyz, cho M(-1;3;4), mặt phẳng (P) đi qua M cắt các trục Ox, Oy, Oz tại các điểm A, B, C sao cho M là trực tâm tam giác ABC. Thể tích khối tứ diện OABC bằng:

A. $\frac{8788}{3}$

B. $\frac{4394}{3}$

C. $\frac{2197}{9}$

D. $\frac{4394}{9}$

Xem lời giải »

Câu 12:

Trong không gian Oxyz, cho 3 điểm $A (0; 1; 1), B (3; 0; - 1), C (0; 21; - 19)$ và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 1)}^{2} = 1$ . Điểm M thuộc mặt cầu (S) sao cho tổng $3 M A^{2} + 2 M B^{2} + M C^{2}$ đạt giá trị nhỏ nhất, khi đó, độ dài vec tơ $\vec{O M}$ là:

A. $\sqrt{110}$

B. $3 \sqrt{10}$

C. $\frac{3 \sqrt{10}}{5}$

D. $\frac{\sqrt{110}}{5}$

Xem lời giải »

Câu 13:

A. $(Q) : 2 y + z = 0$

B. $(Q) : 2 x - z = 0$

C. $(Q) : y - z = 0$

D. $(Q) : 2 y - z = 0$

Xem lời giải »

Câu 14:

Cho ba tia Ox, Oy, Oz đôi một vuông góc với nhau. Gọi C là điểm cố định trên Oz, đặt OC = 1, các điểm A, B thay đổi trên Ox, Oy sao cho OA+ OB = OC. Giá trị bé nhất của bán kính mặt cầu ngoại tiếp tứ diện OABC là:

A. $\frac{\sqrt{6}}{3}$

B. $\sqrt{6}$

C. $\frac{\sqrt{6}}{4}$

D. $\frac{\sqrt{6}}{2}$

Xem lời giải »

Câu 15:

Trong không gian Oxyz, cho A(-4;7;5) và hai đường thẳng $d_{1} : \{\begin{matrix} x = 1 - t \\ y = 3 t \\ z = - 2 + t \end{matrix}, d_{2} : \frac{x + 1}{3} = \frac{y - 2}{4} = z - 1$ . Đường thẳng d đi qua A đồng thời cắt $d_{1}, d_{2}$ có phương trình là:

A. $\{\begin{matrix} x = 2 - 3 t \\ y = - 3 + 5 t \\ z = - 3 + 4 t \end{matrix}$

B. $\{\begin{matrix} x = 2 - 3 t \\ y = 2 + 5 t \\ z = - 1 + 4 t \end{matrix}$

C. $\{\begin{matrix} x = 4 - 4 t \\ y = 7 + 5 t \\ z = 5 + 2 t \end{matrix}$

D. $\{\begin{matrix} x = - 4 - 4 t \\ y = 7 + 5 t \\ z = 5 + 2 t \end{matrix}$

Xem lời giải »

Câu 16:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (1; 0; 3), B (11; - 5; - 12)$ . Điểm $M (a; b; c)$ thuộc mặt phẳng (Oxyz) sao cho $3 M A^{2} + 2 M B^{2}$ nhỏ nhất. Tính $P = a + b + c$

A. P = 5

B. P = 3

C. P = 7

D. P = -5

Xem lời giải »

Câu 17:

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d_{1} : \frac{x - 2}{- 1} = \frac{y}{1} = \frac{z}{1}$ và $d_{2} : \frac{x}{- 2} = \frac{y - 1}{1} = \frac{z - 2}{1}$ . Phương trình mặt phẳng (P) song song và cách đều hai đường thẳng $d_{1}, d_{2}$ là:

A. $2 y - 2 z + 1 = 0$

B. $2 y - 2 z - 1 = 0$

C. $2 x - 2 z + 1 = 0$

D. $2 x - 2 z - 1 = 0$

Xem lời giải »

Câu 18:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 4 x + 10 y - 2 z - 6 = 0$ . Cho m là số thực thỏa mãn giao tuyến của hai mặt phẳng $y = m$ và $x + z - 3 = 0$ tiếp xúc với mặt cầu (S). Tính tất cả các giá trị mà m có thể nhận được bằng:

A. -11

B. -10

C. -5

D. -8

Xem lời giải »

Câu 19:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (2; 0; 0); B (0; 4; 0), C (0; 0; 6)$ . Điểm M thay đổi trên mặt phẳng (ABC) và điểm N là điểm trên tia OM sao cho $O M . O N = 12$ . Biết rằng khi M thay đổi, điểm N luôn thuộc một mặt cầu cố định. Tìm bán kính của mặt cầu đó?

A. $\frac{7}{2}$

B. $3 \sqrt{2}$

C. $2 \sqrt{3}$

D. $\frac{5}{2}$

Xem lời giải »

Câu 20:

Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A (2; - 1; 1), M (5; 3; 1), N (4; 1; 2)$ và mặt phẳng $(P) : y + z = 27$ . Biết rằng tồn tại điểm B trên tia AM, điểm C trên (P) và điểm D trên tia AN sao cho tứ giác ABCD là hình thoi. Tọa độ điểm C là:

A. $(- 15; 21; 6)$

B. $(21; 21; 6)$

C. $(- 15; 7; 20)$

D. $(21; 19; 8)$

Xem lời giải »

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng $(P) : x - 2 y + 2 z + 1 = 0$ , $(Q) : x - 2 y + 2 z - 8 = 0$ , $(R) : x - 2 y + 2 z + 4 = 0$ . Một đường thẳng $∆$ thay đổi cắt ba mặt phẳng $(P), (Q), (R)$ lần lượt tại các điểm A, B, C. Giá trị nhỏ nhất của biểu thức $A B + \frac{96}{A C^{2}}$ là:

A. $\frac{41}{8}$

B. 99

C. 18

D. 24

Xem lời giải »

Câu 22:

Trong không gian Oxyz, cho mặt cầu $(S_{1})$ có tâm $I (2; 1; 1)$ có bán kính bằng 4 và mặt cầu $(S_{2})$ có tâm $J (2; 1; 5)$ có bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu $(S_{1}), (S_{2})$ . Đặt M, m lần lượt là giá trị lớn nhất, nhỏ nhất của khoảng cách từ điểm O đến (P). Giá trị M + m bằng?

A. $8 \sqrt{3}$

B. 9

C. 8

D. $\sqrt{15}$

Xem lời giải »

Câu 23:

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh bên bằng cạnh đáy. Đường thẳng $M N (M \in A' C, N \in B C')$ là đường vuông góc chung của A’C và BC’. Tỉ số $\frac{N B}{N C'}$ bằng:

A. $\frac{3}{2}$

B. $\frac{2}{3}$

C. 1

D. $\frac{\sqrt{5}}{2}$

Xem lời giải »

Câu 24:

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 13}{- 1} = \frac{y + 1}{1} = \frac{z}{4}$ và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 4 y - 6 z - 67 = 0$ . Qua d dựng các mặt phẳng tiếp xúc với (S) lần lượt tại $T_{1}, T_{2}$ . Tìm tọa độ trung điểm H của $T_{1}, T_{2}$

A. $H (8; 1; 5)$

B. $H (2; 10; - 2)$

C. $H (9; 6; 4)$

D. $H (7; - 4; 6)$

Xem lời giải »

Xem thêm bài tập trắc nghiệm Toán 12 có lời giải hay khác:

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Bài tập ôn tập chương III Hình học (mới nhất)

Bài tập ôn tập chương III Hình học

Xem thêm bài tập trắc nghiệm Toán 12 có lời giải hay khác: