Biết F(x) là một nguyên hàm trên R của hàm số f(x) = 2017x / (x^2 +1)^2018
Câu hỏi:
Biết F(x) là một nguyên hàm trên R của hàm số thỏa mãn F(1)=0. Tìm giá trị nhỏ nhất m của F(x)
A.
B.
C.
D.
Trả lời:
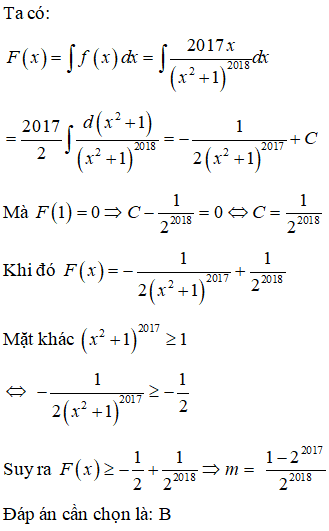
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho ở đó . Giá trị biểu thức là:
Xem lời giải »
Câu 2:
Cho hàm số . Nếu F(x) là một nguyên hàm của hàm số f(x) và đồ thị hàm số y=F(x) đi qua thì là:
Xem lời giải »
Câu 3:
Cho F(x) là một nguyên hàm của hàm số trên tập R và thỏa mãn . Tính tổng
Xem lời giải »
Câu 4:
Cho F(x) là một nguyên hàm của hàm số . Số giá trị của tham số m để và là
Xem lời giải »
Câu 5:
Cho hàm số f(x) thỏa mãn và f(1)=1. Hỏi phương trình có bao nhiêu nghiệm?
Xem lời giải »
