Câu hỏi:
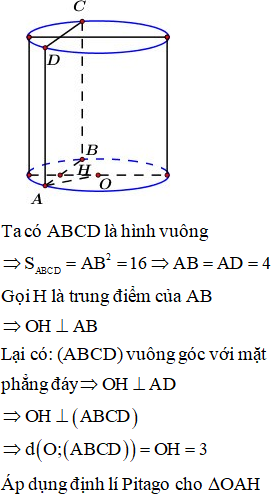
Cắt hình trụ bởi mặt phẳng vuông góc với mặt đáy, ta được thiết diện là hình vuông có diện tích bằng 16. Khoảng cách từ tâm đường tròn đáy của hình trụ đến mặt phẳng bằng 3. Thể tích khối trụ bằng:
A.
B.
C.
D.
Trả lời:
Câu 1:
Thiết diện qua trục của một khối nón là một tam giác vuông cân và có cạnh góc vuông bằng . Thể tích V của khối nón bằng:
Câu 2:
Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn:
Câu 3:
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là . Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí N để diện tích SAM đạt giá trị lớn nhất.
Câu 4:
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng 75% thể tích kem đóng băng ban đầu. Gọi h và r lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số
Câu 5:
Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh a. Tính diện tích toàn phần S của hình trụ.
Câu 6:
Cho mặt cầu tâm O bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C). Hình nón N có đỉnh S nằm trên mặt cầu, có đáy là đường tròn (C) và có chiều cao h (h > R). Tìm h để thể tích khối nón được tạo nên bởi (N) có giá trị lớn nhất.
