Cho hình chóp S.ABC có AB = 5cm, BC = 6cm, CA = 7cm. Hình chiếu
Câu hỏi:
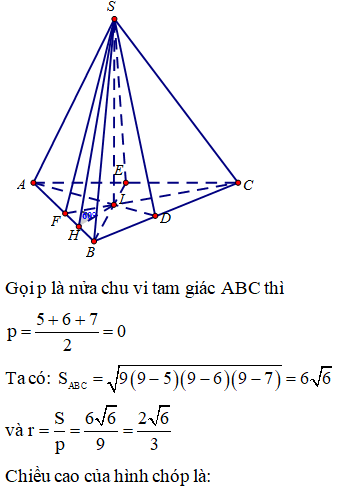
Cho hình chóp S.ABC có AB = 5cm, BC = 6cm, CA = 7cm. Hình chiếu vuông góc của S xuống mặt phẳng (ABC) nằm bên trong tam giác ABC. Các mặt phẳng (SAB), (SBC), (SCA) đều tạo với đáy một góc . Gọi AD, BE, CF là các đường phân giác của tam giác ABC với D ∈ BC, E ∈ AC, F ∈ AB .Thể tích S.DEF gần nhất với số nào sau đây?
A.
B.
C.
D.
Trả lời:
Vì các mặt phẳng (SAB), (SBC), (SCA) đều tạo với đáy một góc và hình chiếu vuông góc của S xuống mặt phẳng (ABC) nằm bên trong tam giác ABC nên ta có hình chiếu của S xuống mặt phẳng (ABC) là tâm đường tròn nội tiếp I của tam giác ABC.

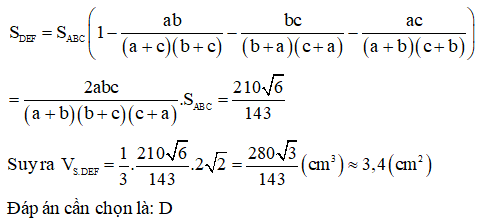
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tứ diện ABCD và G là trọng tâm tam giác ACD. Mặt phẳng (P) qua BG và song song với CD chia khối tứ diện thành hai phần. Tính tỉ số thể tích (số bé chia số lớn) của hai phần đó là:
Xem lời giải »
Câu 2:
Khối chóp S.ABCD có đáy là hình thoi cạnh a, SA=SB=SC=a. Cạnh SD thay đổi. Thể tích khối chóp S.ABCD lớn nhất khi độ dài cạnh SD là:
Xem lời giải »
Câu 3:
Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng , khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và 2, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’ và . Thể tích của khối lăng trụ đã cho bằng:
Xem lời giải »
Câu 4:
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện ABMN. Tính
Xem lời giải »
Câu 5:
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B’ kéo dài lấy điểm M sao cho . Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứ đỉnh A’ có thể tích và khối đa diện chứ đỉnh C’ có thể tích . Tính
Xem lời giải »

