Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, AB = a căn bậc hai 3
Câu hỏi:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC vuông tại A, \[{\rm{A}}B = a\sqrt 3 \], AC = AA’ = a. Sin góc giữa đường thẳng AC’ và mặt phẳng (BCC’B’) bằng:
A. \(\frac{{\sqrt {10} }}{4}\)
B. \(\frac{{\sqrt 6 }}{3}\)
C. \(\frac{{\sqrt 3 }}{3}\)
D. \(\frac{{\sqrt 6 }}{4}\).
Trả lời:
Đáp án đúng là: D
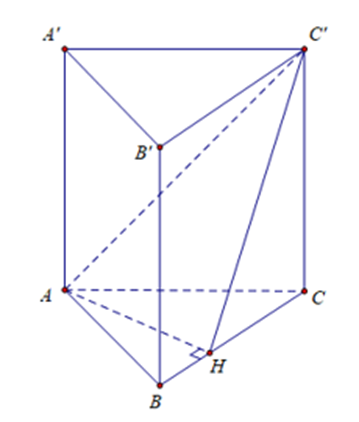
Gọi H là hình chiếu của A trên BC
Ta có AH ⊥ BC, AH ⊥ BB’ nên AH ⊥ (BCC’B’)
Suy ra HC’ là hình chiếu của AC’ trên mặt phẳng (BCC’B’)
Do đó góc giữa AC’ và mặt phẳng (BCC’B’) là góc \(\widehat {AC'H}\)
Vì tam giác ABC vuông tại A nên \[{{\rm{S}}_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]
Vì tam giác ABC vuông tại A nên theo định lý Pytago có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {3{{\rm{a}}^2} + {a^2}} = 2{\rm{a}}\)
Suy ra \(AH = \frac{{AC.AB}}{{BC}} = \frac{{a\sqrt 3 .a}}{{2{\rm{a}}}} = \frac{{a\sqrt 3 }}{2}\)
Vì tam giác AA’C’ vuông tại A’ nên theo định lý Pytago có
\(AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {{{\rm{a}}^2} + {a^2}} = \sqrt 2 {\rm{a}}\)
Xét tam giác AC’H có
\[\sin \widehat {AC'H} = \frac{{AH}}{{AC'}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt 6 }}{4}\]
Vậy ta chọn đáp án D.

