Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D
Câu hỏi:
Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.

A.
B.
C.
D.
Trả lời:
Đáp án C

Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

Xem lời giải »
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=AD=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.
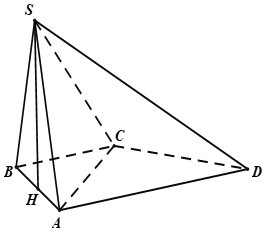
Xem lời giải »
Câu 3:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng
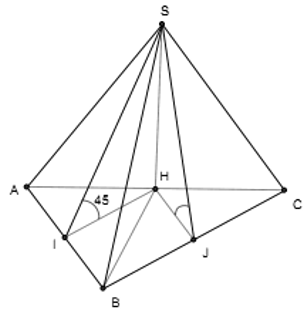
Xem lời giải »
Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 30°, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
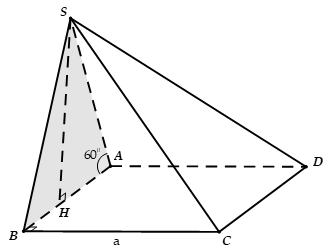
Xem lời giải »
Câu 6:
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD), = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD
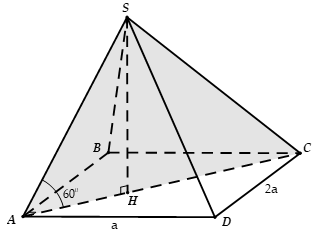
Xem lời giải »
Câu 7:
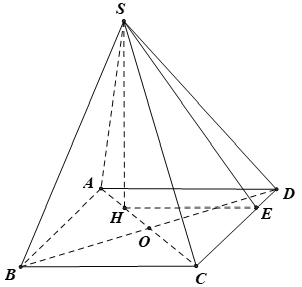
Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm đoạn OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60°. Tính thể tích V của hình chóp S.ABCD
Xem lời giải »
Câu 8:
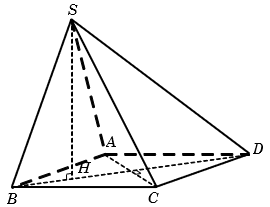
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1, góc = 60°, cạnh bên SD = . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Tính thể tích khối chóp S.ABCD.
Xem lời giải »











