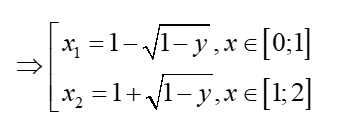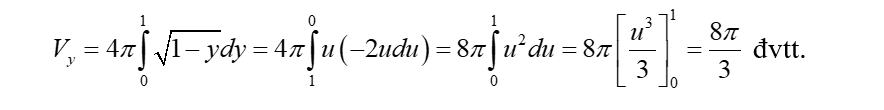Gọi D là miền giới hạn bởi (P): y = 2x - x^2 và trục hoành. Tính thể tích vật thể

❮ Bài trước Bài sau ❯

Câu hỏi:

Gọi D là miền giới hạn bởi (P): y = 2x - x² và trục hoành. Tính thể tích vật thể V do ta quay (D) xung quanh trục Oy.

A. $\frac{12 π}{13}$

B. $\frac{8 π}{3}$

C. $\frac{2 π}{9}$

D. $\frac{π}{15}$

Trả lời:

Chọn B.

0 ≤ x ≤ 2 thì y = 2x – $x^{2}$ ⇔ $x^{2}$ – 2x + y = 0

Phương trình bậc hai theo y. Ta có $△' = 1 - y, y \leq 1$

$V_{y} = π \int_{0}^{1} [{(1 + \sqrt{1 - y})}^{2} - {(1 - \sqrt{1 - y})}^{2}] d y = 4 π \int_{0}^{1} \sqrt{1 - y} d y$

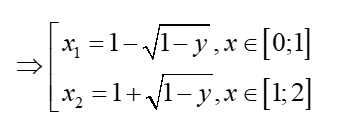
Đặt u = $\sqrt{1 - y} \Rightarrow u^{2} = 1 - y \Rightarrow 2 u d u = - d y$

Đổi cận : khi y = 1 => u = 0; khi y = 0 => u = 1

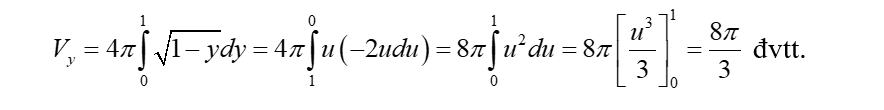
Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = $\sqrt{3}$ , biết thiết diện của vật thể cắt bởi mặt phẳng (P) vuông góc với trục Ox tại điểm có hoành độ x ( $0 \leq x \leq \sqrt{3}$ ) là một hình chữ nhật có độ dài hai cạnh là x và $\sqrt{1 + x^{2}}$

Xem lời giải »

Câu 2:

Cho parabol (P): y= $x^{2} + m$ . Gọi (d) là tiếp tuyến với (P) qua O có hệ số góc k > 0. Xác định m để thể tích vật thể được sinh ra khi hình phẳng giới hạn bởi (P), (d) và trục Oy quay quanh trục Oy bằng 6 $π$ .

Xem lời giải »

Câu 3:

Diện tích hình phẳng giới hạn bởi các đường thẳng y = 1, y = x và đồ thị hàm số $y = \frac{x^{2}}{4}$ trong miền $x \geq 0, y \leq 1$ là phân số tối giản $\frac{a}{b}$ . Khi đó b - a bằng

Xem lời giải »

Câu 4:

Diện tích hình phẳng giới hạn bởi các đường thẳng $y = \{\begin{cases} - x, n ế u x \leq 1 \\ x - 2, n ế u x > 1 \end{cases}$ và y = $\frac{10}{3} x - x^{2}$ là $\frac{a}{b}$ (với $\frac{a}{b}$ là phân số tối giản) . Khi đó a + 2b bằng

Xem lời giải »

Câu 5:

Tổn thương ở vị trí nào không gây ù tai:

Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Gọi D là miền giới hạn bởi (P): y = 2x - x^2 và trục hoành. Tính thể tích vật thể

Xem thêm bài tập Toán có lời giải hay khác: