Tìm tất cả các giá trị thực của m để phương trình 2log 2 |x|+log 2 |x+3|=m
Câu hỏi:
Tìm tất cả các giá trị thực của m để phương trình có 3 nghiệm thực phân biệt:
A.
B.
C.
D.
Trả lời:
TXĐ: D=R
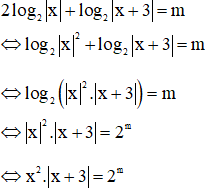
Xét hàm 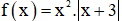 ta có:
ta có: 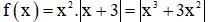
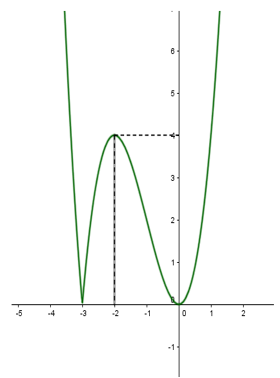
Để phương trình có 3 nghiệm phân biệt thì 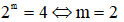
Đáp án cần chọn là: D.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết rằng phương trình có hai nghiệm và . Hãy tính tổng
Xem lời giải »
Câu 2:
Tìm m để phương trình có đúng 2 nghiệm
Xem lời giải »
Câu 3:
Tìm giá trị của tham số m để phương trình có hai nghiệm phân biệt thỏa mãn
Xem lời giải »
Câu 4:
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình sau có 2 nghiệm phân biệt
Xem lời giải »
Câu 5:
Cho thỏa mãn biểu thức . Khi đó x bằng:
Xem lời giải »
Câu 6:
Gọi là các nghiệm của phương trình . Khi đó tích bằng:
Xem lời giải »
Câu 7:
Tìm tất cả các giá trị của tham số m để phương trình có nghiệm
Xem lời giải »
Câu 8:
Tìm tất cả các giá trị thực của tham số m để phương trình có hai nghiệm thỏa mãn
Xem lời giải »
ta có:

