Câu hỏi:
Trong hệ tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;3) và có véc-tơ pháp tuyến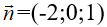 
là:
A. -2x + z + 1 = 0
B. -2y + z - 1 = 0
C. -2x + z - 1 = 0
D. -2x + y - 1 = 0.
Trả lời:
Đáp án C
Phương trình của mặt phẳng cần tìm là -2(x - 1) + 0(y - 2) + 1(z - 3) = 0 <=> -2x + z - 1 = 0.
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình -x+2y+3z-4=0. Mặt phẳng (P) có một véc-tơ pháp tuyến là:
Câu 2:
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng qua A(1;2;-1) có một véc-tơ pháp tuyến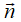 
= (2;0;0) có phương trình là:
Câu 3:
Trong không gian với hệ tọa độ Oxyz, véc-tơ nào dưới đây là một véc-tơ pháp tuyến của mặt phẳng (Oxy)?
Câu 4:
Trong không gian với hệ tọa độ Oxyz, cho M(1;-1;2), N(3;1;-4). Viết phương trình mặt phẳng trung trực của MN.
Câu 5:
Trong không gian Oxyz, cho ba điểm A(4;3;2), B(-1;-2;1) và C(-2;2;-1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
Câu 6:
Trong không gian Oxyz, phương trình mặt phẳng qua ba điểm A(-3;0;0), B(0;-2;0), C(0;0;1) được viết dưới dạng ax + by -6z + c=0. Giá trị của T=a+b-c là:
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;4;-2) và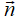 
=(-2;3;-4). Phương trình mặt phẳng (P) đi qua điểm A và nhận 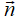làm véc-tơ pháp tuyến là:
Câu 8:
Trong không gian Oxyz, tìm phương trình mặt phẳng (α) cắt ba trục Ox, Oy, Oz lần lượt tại ba điểm A(-3;0;0), B(0;4;0), C(0;0;-2).
