Trong không gian Oxyz, cho hai điểm A(0;-1;2), B(1;1;2) và đường thẳng
Câu hỏi:
Trong không gian Oxyz, cho hai điểm A(0;-1;2), B(1;1;2) và đường thẳng d: . Biết điểm M(a;b;c) thuộc đường thẳng d sao cho tam giác MAB có diện tích nhỏ nhất. Khi đó, giá trị bằng:
A. 10
B. 5
C. 3
D. 4
Trả lời:

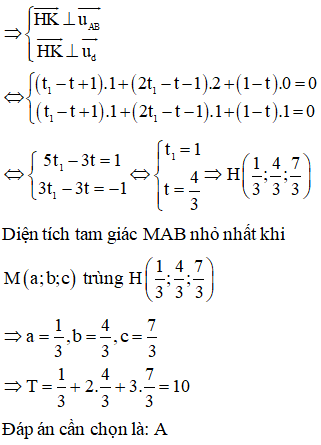
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(-2;3;1), B(5;6;2). Đường thẳng AB cắt mặt phẳng (Oxz) tại điểm M. Tính tỉ số
Xem lời giải »
Câu 2:
Trong không gian với hệ tọa độ Oxyz, gọi là mặt phẳng chứa đường thẳng có phương trình và vuông góc với mặt phẳng . Giao tuyến của và đi qua điểm nào trong các điểm sau:
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song và cách đều hai đường thẳng
Xem lời giải »
Câu 4:
Trong không gian với hệ tọa độ Oxyz, mặt phẳng chắn các trục Ox, Oy, Oz lần lượt tại A, B, C sao cho H(3;-4;2) là trực tâm của tam giác ABC. Phương trình mặt phẳng là:
Xem lời giải »

