Trong không gian Oxyz, cho mặt cầu (S): (x - 2)^2 + (y + 1)^2 + (z + 2)^2 = 4
Câu hỏi:
Trong không gian Oxyz, cho mặt cầu (S): = 4 và mặt phẳng (P): 4x - 3y + m = 0. Với những giá trị nào của m thì mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung?
A. m = -1
B. m = 9 hoặc m = -31
C. m = 1 hoặc m = 21
D. m = -1 hoặc m = -21
Trả lời:
Đáp án D
Mặt cầu (S) có tâm I(2;-1;-2) và có bán kính R=2. Mặt phẳng (P) và mặt cầu (S) có đúng một điểm chung khi và chỉ khi (P) tiếp xúc với (S), từ đó ta được:
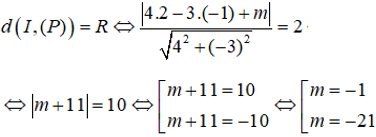
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho hai vectơ = (-1; 3; 4), = (2; -1; 5). Tích có hướng của hai vectơ và là:
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
Xem lời giải »
Câu 3:
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)
Xem lời giải »
Câu 4:
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz
Xem lời giải »
Câu 5:
Trong không gian Oxyz, tìm những điểm M trên trục Ox sao cho khoảng cách từ M đến mặt phẳng (P): x - 2y - 2z + 1 = 0 bằng 2
Xem lời giải »
Câu 6:
Trong không gian Oxyz, tìm những điểm M trên tia Oy sao cho khoảng cách từ điểm M đến mặt phẳng (P): x + 2y - 2z + 1 = 0 bằng 3
Xem lời giải »

