Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1)
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. 2x + y - 3z + 3 = 0
B. x + 2y - z - 1 = 0
C. 3x + 2y - z + 1 = 0
D. 2x - y - 3z + 3 = 0
Trả lời:
Chọn A
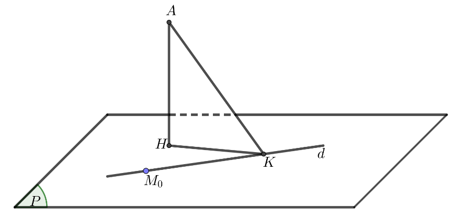
+ d qua M0 (0;0;1) có vectơ chỉ phương 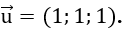
+ Gọi H, K lần lượt là hình chiếu của A lên (P) và d. Ta có: d(A, (P)) = AH ≤ AK
Đẳng thức xảy ra khi và chỉ khi H ≡ K. Do đó d(A, (P))max = AK
Khi đó (P) đi M0 (0;0;1) nhận 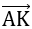 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
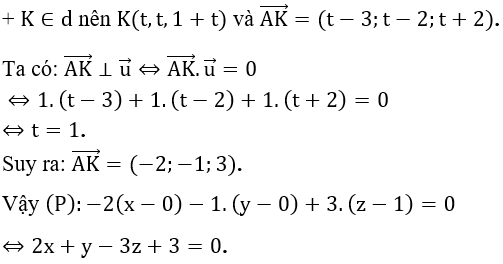
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
Xem lời giải »
Câu 2:
Trong không gian Oxyz, cho ba điểm A(0;0;-1), B(-1;1;0), C(1;0;1). Tìm điểm M sao cho 3MA2 + 2MB2 - MC2 đạt giá trị nhỏ nhất.
Xem lời giải »
Câu 3:
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
Xem lời giải »
Câu 4:
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
Xem lời giải »
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và
Mặt cầu có một đường kính là đoạn thẳng vuông góc chung của d1 và d2 có phương trình là:
Xem lời giải »
Câu 6:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
Xem lời giải »
Câu 7:
Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
Xem lời giải »
Câu 8:
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
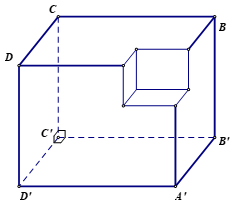
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
Xem lời giải »
làm vectơ pháp tuyến.


