Trong không gian với hệ tọa độ Oxyz, cho đường thẳng delta: x = 2(m^2 - 2m)t
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và điểm A(1;2;3). Gọi S là tập các giá trị thực của tham số m để khoảng cách từ A đến đường thẳng có giá trị nhỏ nhất. Tổng các phần tử của S là:
A.
B.
C.
D.
Trả lời:

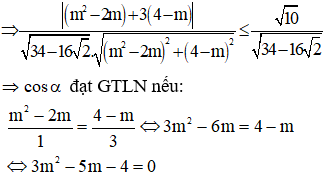
Phương trình này có hai nghiệm phân biệt do ac < 0 nên tổng các giá trị của m là
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Điểm nào sau đây thuộc đường thẳng d?
Xem lời giải »
Câu 2:
Điểm nào sau đây nằm trên đường thẳng
Xem lời giải »
Câu 3:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Đường thẳng d đi qua các điểm nào sau đây?
Xem lời giải »
Câu 4:
Trong không gian Oxyz, đường thẳng đi qua điểm nào dưới đây?
Xem lời giải »
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Vị trí tương đối của và :
Xem lời giải »
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Vị trí tương đối của và là:
Xem lời giải »
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Mệnh đề nào sau đây đúng:
Xem lời giải »
Câu 8:
Trong không gian Oxyz, vị trí tương đối giữa hai đường thẳng và là:
Xem lời giải »

