Xét các số phức z thỏa mãn trị tuyệt đối của (z - 1 + 2i) = căn bậc hai của 5
Câu hỏi:
Xét các số phức z thỏa mãn . Tìm số phức w có mô đun lớn nhất, biết rằng
A. w = 4 - 2i
B. w = -2 + 4i
C. w = 4 - 3i
D. w = 4 + 3i
Trả lời:
Đáp án A
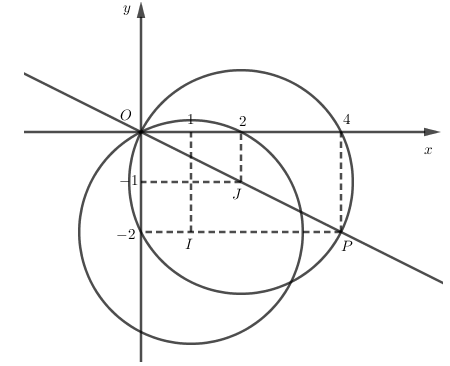
Các điểm M(x; y) biểu diễn z = x + yi có khoảng cách đến điểm I(1; - 2) biểu diễn 1 – 2i bằng nên thuộc đường tròn tâm I bán kính bằng
Từ đó các điểm biểu diễn w thay đổi trên đường tròn tâm J biểu diễn 1 – 2i + 1 + i = 2 - i, bán kính bằng .
Do nên đường tròn này đi qua gốc O
Điểm P biểu diễn w có mô đun lớn nhất khi P là điểm xuyên tâm đối của O trên đường tròn đó tức là w = 2(2 - i) = 4 – 2i
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho số phức thỏa mãn . Tính ab
Xem lời giải »
Câu 2:
Cho số phức z thỏa mãn điều kiện . Tìm giá trị lớn nhất của
Xem lời giải »
Câu 3:
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện và là số thuần ảo?
Xem lời giải »
Câu 4:
Cho các số phức thỏa mãn và . Gọi A, B lần lượt là điểm biểu diễn các số phức . Tính diện tích S của tam giác OAB với O là gốc tọa độ.
Xem lời giải »
Câu 6:
Cho các số phức z thỏa mãn |z + 1 - i| = |z - 1 + 2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
Xem lời giải »


