Cho các số phức z1 = 3i; z2 = m - 2i. Số giá trị nguyên của m để trị tuyệt đối z2

Câu 1:

Gọi A là điểm biểu diễn số phức z = -1 + 6i và B là điểm biểu diễn của số phức z' = -1 - 6i. Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 2:

Cho ba điểm A, B, C lần lượt biểu diễn các số phức sau ${\mathrm{z}}_1$= 1 + i, ${\mathrm{z}}_2$= ${\mathrm{z}}_1^2$, ${\mathrm{z}}_3$= m - i. Tìm các giá trị thực của m sao cho tam giác ABC vuông tại B.

Xem lời giải »

Câu 3:

Cho số phức z. Mệnh đề nào sau đây là đúng?

Xem lời giải »

Câu 4:

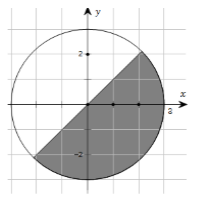
Gọi M là điểm biểu diễn của số phức z, biết tập hợp các điểm M là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng?

Xem lời giải »

Câu 5:

Tính mô đun của số phức $\mathrm{w}={\left(1-\mathrm{i}\right)}^2\mathrm{z}$. Biết số phức z có mô đun bằng m

Xem lời giải »

Câu 6:

Cho số phức z = $\left(\mathrm{m}+3\right)+\left({\mathrm{m}}^2-\mathrm{m}-6\right)\mathrm{i}$ với $\mathrm{m}\in \mathrm{R}$. Gọi (P) là tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi (P) và trục hoành bằng

Xem lời giải »

Câu 7:

Tìm các số thực x, y thỏa mãn đẳng thức 3x + y + 5xi = 2y - (x - y)i

Xem lời giải »

Câu 8:

Trong mặt phẳng phức, gọi A, B, C lần lượt là các điểm biểu diễn của các số phức ${\mathrm{z}}_1=3+2\mathrm{i};$${\mathrm{z}}_2=3-2\mathrm{i};$${\mathrm{z}}_3=-3-2\mathrm{i}$. Khẳng định nào sau đây là sai?

Xem lời giải »