Cho f(x)=4m/π+sin^2 x. Tìm để nguyên hàm của hàm số thỏa mãn F(0)=1 và F(π/4)=π/8

Câu hỏi:

Cho $f (x) = \frac{4 m}{π} + \sin^{2} x$ .Tìm m để nguyên hàm của hàm số f(x) thỏa mãn F(0)=1 và $F (\frac{π}{4}) = \frac{π}{8}$

A. -3/4

B. 3/4

C. -4/3

D. 4/3

Trả lời:

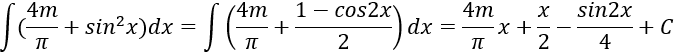
Vì F(0) = 1 nên C =1

$F (\frac{π}{4}) = \frac{π}{8}$ nên tính được m = -3/4

Chọn A.

Câu 1:

Kết quả tính $\int \frac{- x^{3} + 5 x + 2}{4 - x^{2}} d x$ bằng

Câu 2:

Tìm nguyên hàm của hàm số $f (x) = \sin^{3} x . \sin 3 x$ .

Câu 3:

Họ nguyên hàm của hàm số $f (x) = \frac{x^{2} + x + x^{3} + 1}{x^{3}}$ là hàm số nào?

Câu 4:

Giá trị m để hàm số $F (x) = m x^{3} + (3 m + 2) x^{2} - 4 x + 3$ là một nguyên hàm của hàm số $f (x) = 3 x^{2} + 10 x - 4$

Câu 5:

Tìm nguyên hàm của hàm số $f (x) = \frac{1}{\sin x . \cos x}$ .

Câu 6:

Tìm nguyên hàm của hàm số $f (x) = \frac{2 \sin^{3} x}{1 + \cos x} .$

Câu 7:

Tìm nguyên hàm của hàm số $f (x) = \frac{\cos^{3} x}{\sin^{5} x} .$

Câu 8:

Tìm nguyên hàm của hàm số: $f (x) = \cos 2 x (\sin^{4} x + \cos^{4} x) .$

Các dạng bài tập Toán lớp 12