Cho hàm số y = f (x) liên tục trên [a;b]. Giả sử hàm số u = u(x)
Câu hỏi:
Cho hàm số y = f (x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A.
B.
C.
D.
Trả lời:
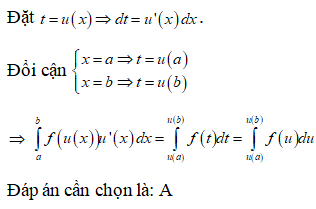
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho số thực a thỏa mãn , khi đó a có giá trị bằng
Xem lời giải »
Câu 4:
Hàm số y = f (x) có nguyên hàm trên (a;b) đồng thời thỏa mãn f(a)=f(b). Lựa chọn phương án đúng:
Xem lời giải »
Câu 6:
Cho tích phân , nếu đặt thì
Xem lời giải »
Câu 7:
Để tính theo phương pháp tích phân từng phần, ta đặt:
Xem lời giải »
Câu 8:
Cho f(x), g(x) là hai hàm số có đạo hàm liên tục trên đoạn [0;1] và thỏa mãn điều kiện . Tính tích phân ?
Xem lời giải »

