Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC

Câu hỏi:

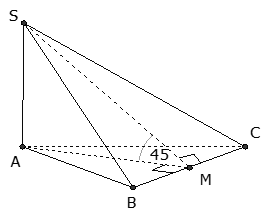
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a $\sqrt{2}$ , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng

A. $\frac{a^{3} \sqrt{2}}{6}$

B. $\frac{a^{3} \sqrt{2}}{2}$

C. $\frac{a^{3} \sqrt{2}}{4}$

D. $\frac{a^{3} \sqrt{2}}{12}$

Trả lời:

Đáp án D

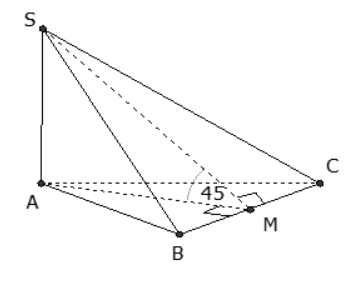
Gọi M là trung điểm của BC

Vì $∆ A B C$ cân tại A nên $A M ⊥ B C$

Ta có: $S A ⊥ (A B C D) \Rightarrow S A ⊥ B C$

Mà $A M ⊥ B C$

nên $B C ⊥ (S A M) \Rightarrow B C ⊥ S M \Rightarrow \hat{((S B C); (A B C D))} = \hat{S M A} = 45 °$

Xét $∆ A B C$ vuông cân tại A, có $B C = a \sqrt{2}$

$\Rightarrow A B = A C = a v à A M = \frac{a}{\sqrt{2}}$

Xét $∆ S A M$ vuông tại A, ta có:

$\tan \hat{S M A} = \frac{S A}{A M} \Rightarrow S A = A M . \tan \hat{S M A} = \frac{a}{\sqrt{2}}$

Thể tích khối chóp SABCD là: $V_{S A B C D} = \frac{1}{3} . S_{∆ A B C} . S A = \frac{1}{3} . \frac{1}{2} . a . a . \frac{a}{\sqrt{2}} = \frac{a^{3} \sqrt{2}}{12}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng $\sqrt{3}$ a/4. Thể tích của hình chóp S.ABC là:

Xem lời giải »

Câu 2:

Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a $\sqrt{2}$ . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

Xem lời giải »

Câu 3:

Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a $\sqrt{2}$ . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.

Xem lời giải »

Câu 4:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a $\sqrt{2}$ , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4 $a^{3}$ /3. Tính khoảng cách h từ B đến mặt phẳng (SCD).

Xem lời giải »

Câu 5:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC cân tại A. Cạnh bên SB lần lượt tạo với mặt phẳng đáy, mặt phẳng trung trực của BC các góc bằng 30° và 45°, khoảng cách từ S đến cạnh BC bằng a. Tính thể tích khối chóp S.ABC

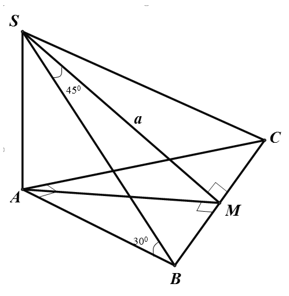
Xem lời giải »

Câu 6:

Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.

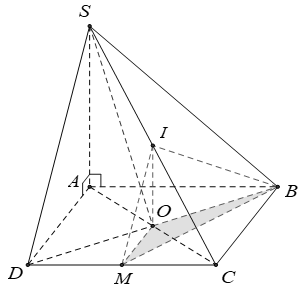
Xem lời giải »

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 12

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC

Xem thêm bài tập Toán có lời giải hay khác: