Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a.
A. V =
B. V =
C. V =
D. V =
Trả lời:
Chọn D
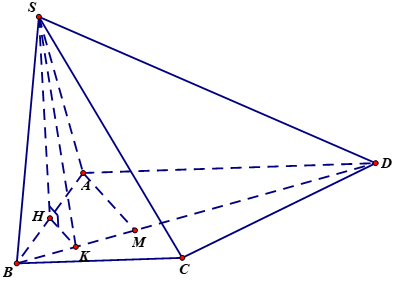
Ta có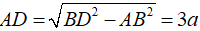 
Gọi H là trung điểm AB thì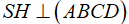 
,
kẻ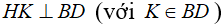 
, ta có 
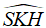là góc giữa (SBD) và (ABCD), do đó 
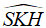= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
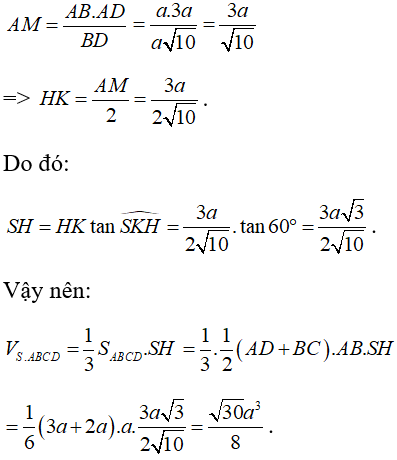
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng . Thể tích Vcủa khối chóp S.ABCD là:
Xem lời giải »
Câu 2:
Khối chóp S.ABCD có đáy là hình thoi cạnh a, SA = SB = SC = a, cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:
Xem lời giải »
Câu 3:
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng:
Xem lời giải »
Câu 4:
Hình lăng trụ đứng ABC.A'B'C' có diện tích đáy bằng 4, diện tích ba mặt bên lần lượt là 9, 18 và 10. Thể tích khối lăng trụ ABC.A'B'C' bằng:
Xem lời giải »
