Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC)
Câu hỏi:
A.
B.
C.
D.
Trả lời:
Chọn D
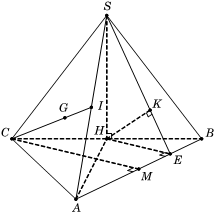
Ta có
Tam giác ABC đều cạnh a nên
Trong tam giác vuông SHA, ta có
Vì mặt cầu có tâm G và tiếp xúc với nên bán kính mặt cầu
Ta có
Gọi M, E lần lượt là trung điểm AB và MB
Suy ra và
Gọi K là hình chiếu vuông góc của H trên SE, suy ra . (1)
Ta có (2)
Từ (1) và (2), suy ra nên
Trong tam giác vuông SHE, ta có
Vậy