Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng
Câu hỏi:
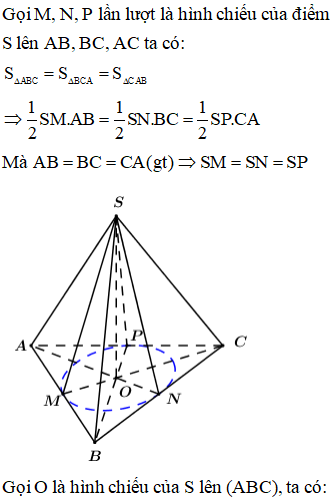
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng . Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng . Tính thể tích nhỏ nhất của khối chóp S.ABC
A. 3
B.
C.
D. 4
Trả lời:

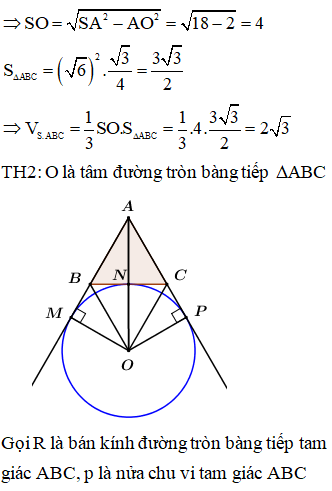


Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tứ diện SABC và G là trọng tâm của tứ diện, mặt phẳng quay quanh AG và cắt các cạnh SB, SC tương ứng tại M, N. Giá trị nhỏ nhất của tỉ số là
Xem lời giải »
Câu 2:
Cho hình chóp S.ABC có . Tính thể tích khối chóp S.ABC
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt đáy nằm trong hình vuông ABCD. Biết rằng SA và SC tạo với đáy các góc bằng nhau, góc giữa SB và đáy bằng , góc giữa SD và đáy bằng với . Tính thể tích khối chóp đã cho.
Xem lời giải »
Câu 4:
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và có thể tích . Tìm số r > 0 sao cho tồn tại điểm J nằm trong khối chóp mà khoảng cách từ J đến các mặt bên và mặt đáy đều bằng r?
Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD song song với BC, . Gọi E, F là hai điểm lần lượt nằm trên các cạnh AB và AD sao cho (E, F không trùng với A). Tổng giá trị lớn nhất và giá trị nhỏ nhất của tỉ số thể tích hai khối chóp S.BCDFE và S.ABCD là:
Xem lời giải »
Câu 6:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, . Cạnh bên SC vuông góc với đáy, góc giữa SA và đáy bằng . Thể tích khối chóp đó bằng:
Xem lời giải »
Câu 7:
Cho hình chóp S.ABCD có đáy là hình thoi cạnh bằng 2, và tam giác SBD vuông cân tại S. Gọi E là trung điểm của SC. Mặt phẳng (P) qua AE và cắt hai cạnh SB, SD lần lượt tại M và N. Thể tích lớn nhất của khối đa diện ABCDNEM bằng:
Xem lời giải »
Câu 8:
Cho tứ diện ABCD có , tam giác ACD đều, hình chiếu vuông góc của A lên mặt phẳng (BCD) trùng với trực tâm H của tam giác BCD, mặt phẳng (ADH) tạo với mặt phẳng (ACD) một góc . Tính thể tích khối tứ diện ABCD.
Xem lời giải »

