Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a

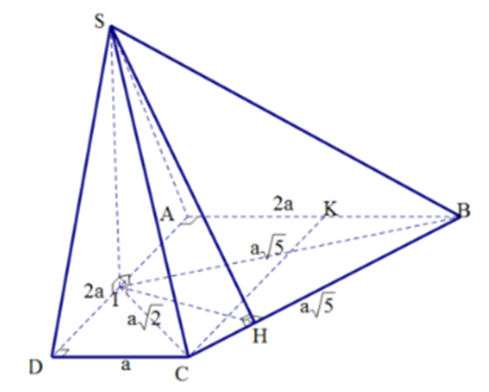
Gọi K là trung điểm đoạn AB ; H là chân đường cao kè từ I của tam giác IBC

Hai mặt phẳng (SBI) và (SCI) cùng vuông góc với đáy nên ta suy ra \(SI \bot (ABCD)\)

Ta có:

\(\begin{array}{l}{S_{ABCD}} = \frac{{(CD + AB).AD}}{2} = \frac{{\left( {a + 2{\rm{a}}} \right).2{\rm{a}}}}{2} = 3{a^2}\\{V_{S.ABCD}} = \frac{1}{3}SI.{S_{ABCD}} \Leftrightarrow \frac{{3\sqrt {15} {a^3}}}{5} = \frac{1}{3}.SI.3{{\rm{a}}^2}\\ \Rightarrow SI = \frac{{3\sqrt {15} a}}{5}\end{array}\)

Vì \(\left\{ {\begin{array}{*{20}{l}}{(SBC) \cap (ABCD) = BC}\\{BC \bot (SIH)}\\{(SIH) \cap (SBC) = SH}\\{(SIH) \cap (ABCD) = IH}\end{array}} \right.\) nên góc giữa hai mặt phẳng (SBC) và (ABCD) là \(\widehat {SHI}\)

Vì K là trung điểm của AB nên AK = BK = a

Mà CD = a suy ra AK = CD

Mà AK // CD (vì cùng vuông góc với AD)

Suy ra AKCD là hình bình hành

Lại có \(\widehat {A{\rm{DC}}} = 90^\circ \) nên AKCD là hình chữ nhật

Do đó CK = AD = 2a và \(CK \bot AB\)

Suy ra tam giác CBK vuông tại K. Theo định lý Pytago có

\(BC = \sqrt {B{K^2} + C{K^2}} = \sqrt {{a^2} + 4{{\rm{a}}^2}} = a\sqrt 5 \)

Ta có \[{{\rm{S}}_{IBC}} = {S_{ABC{\rm{D}}}} - {S_{ABI}} - {S_{C{\rm{D}}I}} = 3{{\rm{a}}^2} - \frac{1}{2}.a.2{\rm{a}} - \frac{1}{2}.a.a = \frac{3}{2}{a^2}\]

\({S_{IBC}} = \frac{1}{2}IH.BC \Rightarrow IH = \frac{{2{{\rm{S}}_{IBC}}}}{{BC}} = \frac{{3{{\rm{a}}^2}}}{{a\sqrt 5 }} = \frac{{3a}}{{\sqrt 5 }}\)

Xét tam giác SHI có:

\(\tan \widehat {SHI} = \frac{{SI}}{{HI}} = \frac{{\frac{{3\sqrt {15} a}}{5}}}{{\frac{{3{\rm{a}}}}{{\sqrt 5 }}}} = \sqrt 3 \)

Suy ra \(\widehat {SHI} = 60^\circ \)

Do đó giữa hai mặt phẳng (SBC) và (ABCD) là 60°

Vậy ta chọn đáp án D.