Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K

Câu hỏi:

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K. Tính tỉ số

\frac{K S}{K A}

Trả lời:

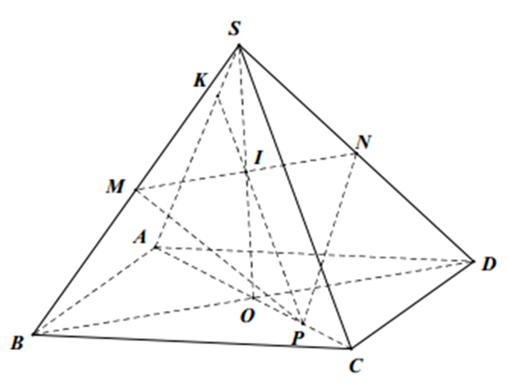
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K (ảnh 1)

Trong mặt phẳng (SBD), gọi I là giao điêm của MN và SO

Ta có SA ⊂ (SAC); (MNP) ∩ (SAC) = PI

SA ⊂ (SAC); (MNP) ∩ (SAC) = PI

Trong mặt phẳng (SAC), PI cắt SA tại K ⇒ K là giao điểm của SA và (MNP)

Mặt khác: MN là đường trung bình của tam giác SBD nên MN cắt SO tại trung điểm I

⇒ PI là đường trung bình của tam giác ⇒ PI // SC hay PK // SC.

$\Rightarrow \frac{K S}{K A} = \frac{P C}{P A} = \frac{\frac{1}{4} A C}{\frac{3}{4} A C} = \frac{1}{3}$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC.

a) Tìm giao điểm I của AM và (SBD).

b) Tìm giao điểm P của SD và (ABM). Chứng minh rằng P là trung điểm của SD.

c) Gọi N là điểm tùy ý trên cạnh AB. Tìm giao điểm K của MN và (SBD).

Xem lời giải »

Câu 2:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K, J lần lượt là trọng tâm tam giác ABC và tam giác SBC. Xác định thiết diện hình chóp cắt bởi mặt phẳng chứa KI và song song AD.

Xem lời giải »

Câu 3:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.

Xem lời giải »

Câu 4:

Cho hình chóp S.ABCD có đáy là hình thang (AB//CD và AB = 3CD). Gọi H là điểm thuộc cạnh SC sao cho SH = 3HC. Gọi K là giao điểm của SB và (ADH). Tính tỉ số