Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC. a) Tìm giao điểm I của AM và (SBD).

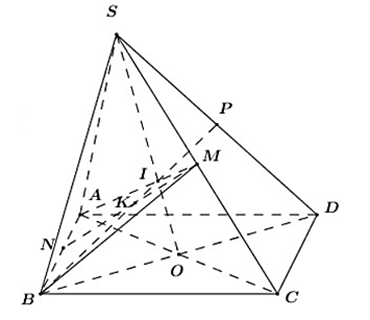
a) Trong (ABCD) gọi O = AC ∩ BD. Suy ra SO ⊂ (SAC), SO ⊂ (SBD)

Trong (SAC) gọi I = AM ∩ SO ta có:

I ∈ AM, I ∈ SO ⊂ (SBD)

Nên I ∈ (SBD)

Suy ra: I = AM ∩ (SBD)

b) Trong (SBD) gọi P = BI ∩ SD ta có:

P ∈ SD

P ∈ BI ⊂ (ABM) nên P ∈ (ABM)

Suy ra: P = SD ∩ (ABM)

Ta có: I là trọng tâm tam giác SAC nên $\frac{SI}{SO}=\frac{2}{3}$

Xét tam giác SBD có SO là trung tuyến ứng với cạnh BD, $\frac{SI}{SO}=\frac{2}{3}$

Nên I là trọng tâm tam giác SBD

Suy ra: BI là trung tuyến của tam giác SBD ứng với cạnh SD

Mà BI ∩ SD = P nên P là trung điểm của SD.

c) Trong (SBD) gọi K = MN ∩ BP ta có:

K ∈ MN

K ∈ BP ⊂ (SBD) nên K ∈ (SBD)

Vậy K = MN ∩ (SBD).