Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có SA tạo với đáy một góc bằng 30o và SA=2a. Trong các điểm S, B, C điểm nào nằm trong mặt cầu tâm A bán kính 3a.
A. Không điểm nào
B. Chỉ điểm S
C. Chỉ hai điểm B và C
D. Cả ba điểm
Trả lời:
Đáp án C
Gọi O là tâm của tam giác đều ABC.
Nên:
Ta có: = 30o => AO = a => AB = AC = 3a
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho mặt cầu tâm O bán kính R và điểm A bất kì trong không gian. Điểm A không nằm ngoài mặt cầu khi và chỉ khi:
Xem lời giải »
Câu 2:
Cho hình chóp S.ABC có đáy là tam giác vuông cân đỉnh B và BC = a, SA ⊥ (ABC), SA = 2a. Khẳng định nào sau đây là đúng?
Xem lời giải »
Câu 3:
Cho mặt cầu (S) tâm O bán kính R và một mặt phẳng (P). Kí hiệu h là khoảng cách từ O đến mặt phẳng (P). Mặt phẳng (P) có nhiều hơn một điểm chung với mặt cầu (S) nếu:
Xem lời giải »
Câu 4:
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
Xem lời giải »
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng 2a, DSAB là tam giác đều. Bán kính mặt cầu tâm A cắt SB theo một dây có độ dài a là:
Xem lời giải »
Câu 6:
Cho đường tròn (C) ngoại tiếp một tam giác đều ABC có cạnh bằng a, chiều cao AH. Quay đường tròn (C) xung quanh trục AH, ta được một mặt cầu. Thể tích của khối cầu tương ứng là:
Xem lời giải »
Câu 7:
Cho tam giác ABC vuông tại A có BC = 2a và = 30°. Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi là diện tích toàn phần của hình nón đó và là diện tích mặt cầu có đường kính AB. Khi đó, tỉ số 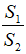 là:
là:
Xem lời giải »
Câu 8:
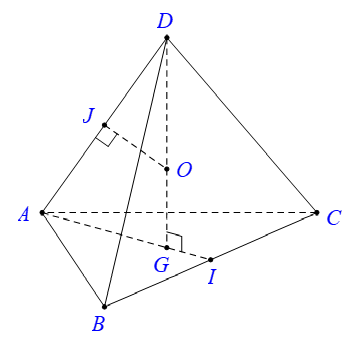
Tính bán kính của mặt cầu ngoại tiếp hình tứ diện đều cạnh a.
Xem lời giải »



