Cho hình nón có đường cao h = 5a và bán kính đáy r = 12a. Gọi (alpha) là mặt phẳng

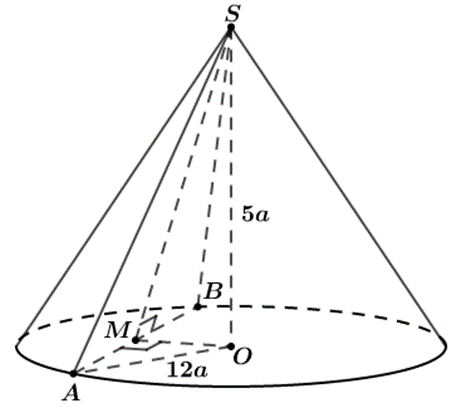
Gọi S là đỉnh của hình nón và O là tâm của đường tròn đáy

Giả sử mặt phẳng (α) cắt hình nón theo một thiết diện là tam giác SAB cân tại S

Theo giả thiết ta có: SO = 5a, OA = OB = 12a và AB = 10a

Gọi M là trung điểm của AB

Suy ra $MA = MB = \frac{{AB}}{2} = \frac{{10{\rm{a}}}}{2} = 5{\rm{a}}$

Tam giác OAB cân tại O có OM là trung tuyến

Suy ra OM là đường cao. Hay OM ⊥ AB

Vì tam giác AOM vuông tại M nên $O{M^2} = O{A^2} - M{A^2} = 144{{\rm{a}}^2} - 25{{\rm{a}}^2} = 119{{\rm{a}}^2}$

Vì tam giác SOM vuông tại O nên ${\rm{S}}M = \sqrt {S{O^2} + O{M^2}} = \sqrt {25{{\rm{a}}^2} + 119{{\rm{a}}^2}} = 12{\rm{a}}$

Tam giác SAB cân tại S có SM là trung tuyến

Suy ra SM là đường cao

Do đó diện tích tam giác SAB là $S = \frac{1}{2}SM.AB = \frac{1}{2}.12{\rm{a}}.10{\rm{a}} = 60{a^2}$

Vậy ta chọn đáp án C.