Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao
Câu hỏi:
Cho hình nón đỉnh I và đường tròn đáy tâm O. Bán kính đáy bằng chiều cao của hình nón. Giả sử khoảng cách từ trung điểm của IO tới một đường sinh bất kì là . Hai điểm A, B nằm trên đường tròn tâm O sao cho AB = 1/2. Tính thể tích khối tứ diện IABO
A.
B.
C.
D.
Trả lời:
Đáp án C
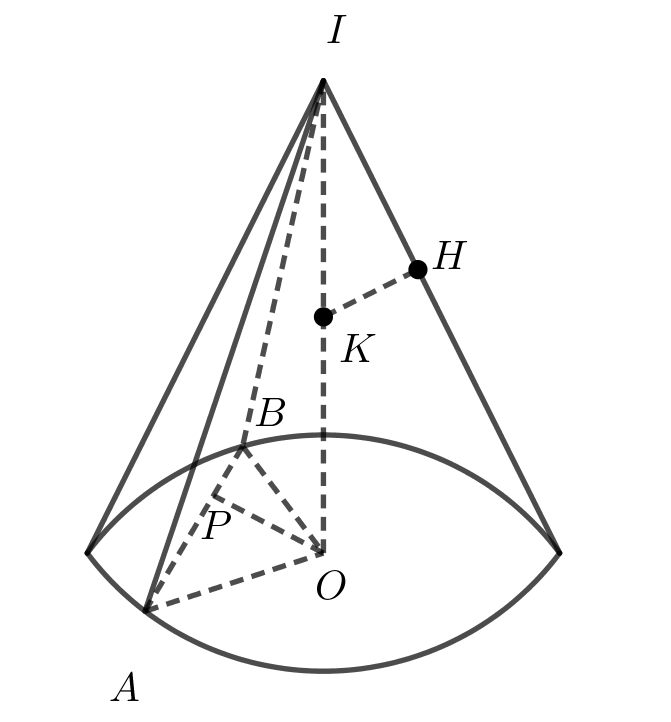
Gọi K là trung điểm của IO
Do bán kính đáy (r) = chiều cao hình nón (h)
nên tam giác thiết diện qua trục là tam giác vuông cân
Xét, có: OB = OA = 4; AB =
Nửa chu vi:
Khi đó, diện tích là:
Thể tích hình chóp IOAB là:
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một hình chóp có 40 cạnh. Hình chóp đó có bao nhiêu mặt?
Xem lời giải »
Câu 5:
Có ba quả bóng đá hình cầu có cùng bán kính r được xếp tiếp xúc với nhau từng đôi một. Trong các rổ hình trụ có chiều cao 2r và bán kính R, hỏi bán kính R nhỏ nhất là bao nhiêu để hình trụ có thể chứa được cả ba quả bóng đó?
Xem lời giải »
Câu 6:
Trong không gian Oxyz, cho ba điểm A(1; 2; 0), B(-2; 1; 3), C(7; -3; -6). Viết phương trình tham số của đường thẳng d đi qua trọng tâm G của tam giác ABC, đồng thời d song song với hai mặt phẳng (Oxy) và (Oxz)
Xem lời giải »
Câu 7:
Trong không gian Oxyz, cho ba điểm A(1; -2; 3), B(0; 1; 5), C(4; -1; 7). Gọi M là trung điểm của BC. Viết phương trình tham số của đường thẳng AM
Xem lời giải »
Câu 8:
Trong không gian Oxyz, viết phương trình tham số của đường thẳng d đi qua điểm M(1;2;-3) và d vuông góc với mặt phẳng (P): 3x + y + 1 = 0
Xem lời giải »


