Cho hình phẳng (H) giới hạn bởi parabol y=ax^2 +1 (a>0), trục tung
Câu hỏi:
Cho hình phẳng (H) giới hạn bởi parabol trục tung và đường thẳng x = 1. Quay (H) quanh trục Ox được một khối tròn xoay có thể tích bằng . Mệnh đề nào dưới đây đúng?
A. 2 < a < 3
B. 0 < a < 2
C. 5 < a < 8
D. 3 < a < 5
Trả lời:
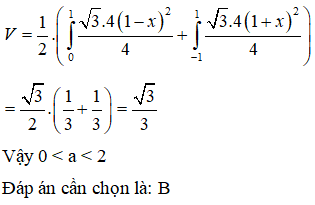
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và
Xem lời giải »
Câu 2:
Thể tích vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x là một nửa đường tròn đường kính bằng:
Xem lời giải »
Câu 3:
Cho hình phẳng giới hạn bởi . Thể tích vật tròn xoay khi D quay quanh trục Ox là: với . Tính
Xem lời giải »
Câu 4:
Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình bên)
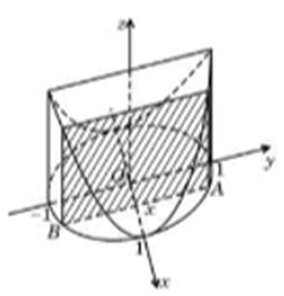
Xem lời giải »
Câu 5:
Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y=tanx, trục Ox, đường thẳng x = 0, đường thẳng quanh trục Ox là:
Xem lời giải »
Câu 6:
Tính thể tích khi quay quanh trục Ox
Xem lời giải »
Câu 7:
Gọi H là hình phẳng giới hạn bởi parabol và đường thẳng y = 2x. Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành
Xem lời giải »
Câu 8:
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b] với a < b. Kí hiệu là diện tích hình phẳng giới hạn bởi các đường y = 3f(x), y = 3g(x), x = a, x = b, là diện tích hình phẳng giới hạn bởi các đường y = f(x) − 2, y = g(x) − 2, x = a, x = b. Khẳng định nào sau đây đúng?
Xem lời giải »

